Team:SUSTC-Shenzhen-A/Modeling
From 2013.igem.org
| Line 220: | Line 220: | ||
</div> | </div> | ||
<p>Our model is to simulate an E coli cell-cell mutual help system that we are implementing to study the class game theory problem of prisoner's dilemma. Speciafically we designed two types of E coli cells to act as the two “prisoners” in a single enclosed environment with toxic chemical . The behavior of each “prisoner” under isolated interrogation is designed with constitutive promoter of different strength, with the weaker promoter mimic defect and the stronger promoter mimics cooperates. The results of such promoter is to detox the other cell while poison itself. The fate of one “prisoner” is related to the growth rate or density of one particular cell. We used mathematic modeling to quantitatively explore the consequence of each strategy of the classic prisoner’s dilemma. </p> | <p>Our model is to simulate an E coli cell-cell mutual help system that we are implementing to study the class game theory problem of prisoner's dilemma. Speciafically we designed two types of E coli cells to act as the two “prisoners” in a single enclosed environment with toxic chemical . The behavior of each “prisoner” under isolated interrogation is designed with constitutive promoter of different strength, with the weaker promoter mimic defect and the stronger promoter mimics cooperates. The results of such promoter is to detox the other cell while poison itself. The fate of one “prisoner” is related to the growth rate or density of one particular cell. We used mathematic modeling to quantitatively explore the consequence of each strategy of the classic prisoner’s dilemma. </p> | ||
| - | + | </div> | |
| - | + | ||
<div class="bs-docs-section"> | <div class="bs-docs-section"> | ||
<div class="page-header"> | <div class="page-header"> | ||
| Line 240: | Line 239: | ||
</div> | </div> | ||
<p>We model the density dynamics of the two cells over time based on the degree of their collaboration. Our model is consistent of ordinary differential equations for the densities of two cell types and two AHLs. The detailed description of all the equations and parameters are described here </p> | <p>We model the density dynamics of the two cells over time based on the degree of their collaboration. Our model is consistent of ordinary differential equations for the densities of two cell types and two AHLs. The detailed description of all the equations and parameters are described here </p> | ||
| + | <a href="/File:Modelingsustc5.png" class="image"><img alt="Modelingsustc5.png" src="/wiki/images/0/0c/Modelingsustc5.png" width="342" height="475"></a> | ||
| + | |||
</div> | </div> | ||
Revision as of 02:13, 28 September 2013
Game theory
Stategy for the Classic Prisoners' Dilemma.
Abstract
Our model is to simulate an E coli cell-cell mutual help system that we are implementing to study the class game theory problem of prisoner's dilemma. Speciafically we designed two types of E coli cells to act as the two “prisoners” in a single enclosed environment with toxic chemical . The behavior of each “prisoner” under isolated interrogation is designed with constitutive promoter of different strength, with the weaker promoter mimic defect and the stronger promoter mimics cooperates. The results of such promoter is to detox the other cell while poison itself. The fate of one “prisoner” is related to the growth rate or density of one particular cell. We used mathematic modeling to quantitatively explore the consequence of each strategy of the classic prisoner’s dilemma.
So, how do we emulate this prisoner’s dilemma using genetically engineered E coli?
The toxic chemical is antibiotics Zeocin, which can be detox with the expression an antidote gene (zeo-resistent gene) to neutralized Zeocin. Without the antidote, the cell will either grow slower or die, with the antidote, it would grow happily. If “prisoner A” is collaborative to “prisoner B’, it would have a strong promoter to express an enzyme LasI to produce 12-carbon AHL (3OC12-HSL), a quorum sensing molecule to help B’s survive and grow in the environment. In the mean time, A itself makes sacrifice by also express an toxic protein that only worked on itself. The beneficial cell B utilizes the 3OC12-HSL to turn on an antidote gene (zeo-resistent gene) to protect the cell from the toxic chemical. If A cell is the traitor, it would not produce 3OC12-HSL that could help B cell, and in the meantime prevent production of toxic protein to itself. We use tetA, a tetracycline transporter which could also transport toxic Nickel ion into cell as the toxic protein. The B cell has the same design except that it expresses enzyme LusI to produce a different AHL (3OC6-HSL) and senses the 3OC12-HSL. The A cell can sense 3OC6-HSL and produce the antidote to zeo. The diagram is shown in the Figure xxx. The cell with more antidote protein and/or less toxic protein will grow faster, which in our system suffer less “jail time”.
The reason to use mathematic modeling
As a whole system, it is the mutual interest for both to cooperate. However if one chooses to cooperate, it may risk that other would enjoy its collaboration but defect it. It’s a complex problem that how our prisoners choose their strategies to ensure their survival. We would like to explore various strategies and the consequences using mathematic models so as to explain experimental data. We also want to find interesting alternative phenomena that do not exist in the classic prisoner’s dilemma.
the model
We model the density dynamics of the two cells over time based on the degree of their collaboration. Our model is consistent of ordinary differential equations for the densities of two cell types and two AHLs. The detailed description of all the equations and parameters are described here

Test
To confirm whether our simulations can work out a good result, we want to test some important parameters to see whether our subsystem can work properly,
1.the effect of Zeocin
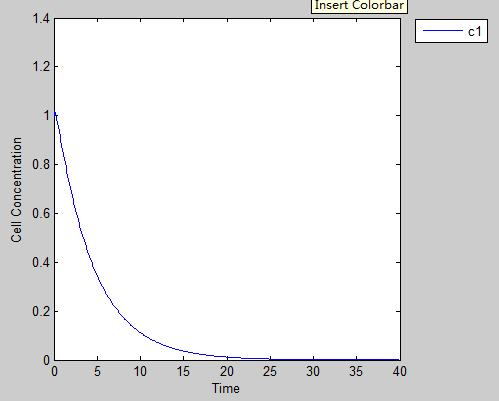
We put our prisoners into a person to see what will happen to this poor man, this will help us understand how powerful the punishment is as well as tell us how much Zeocin we should use to create a temperate environment stress. As we can see from this figure, this antibiotic leads to a quick death of our prisoner. Without help, one man can hardly get out of this problem.
2.separate cell in the environment contain AHL
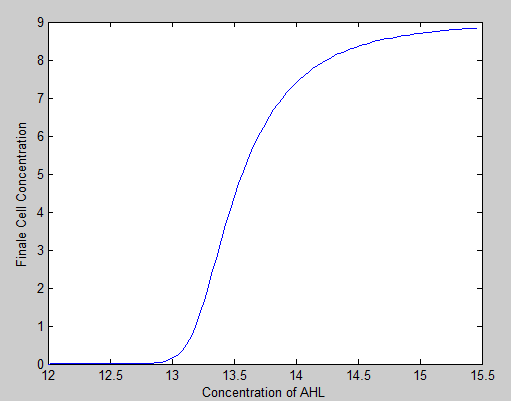
To test our relationship between the concentration of AHL and the concentration of our cells, we conduct this test. We put one of our prisoners into AHL concentration gradients to make sure where the efficient concentration of AHL lies, and we get the final cell concentration for each AHL gradients.
This EC can tell us some important things such as whether there exists any sensitivity difference of AHL between the two cells, it can help us have a better understanding of the cooperation between these two cells. As we can see there is a cliffy slope in our data, which give us the idea that the relationship between the AHL and cell concentration is not simply linear, so we should consider twice before we change this influential variable.
3.the show begins
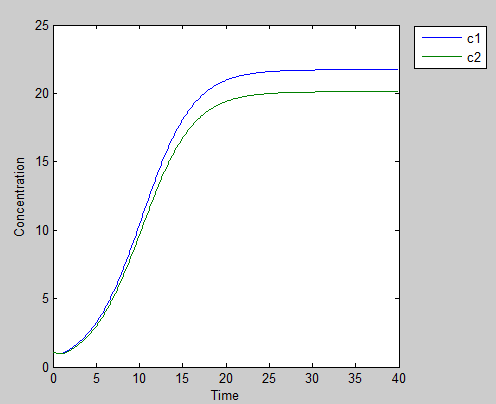
Result 1:Good Cooperation
If both of our prisoners try to help each other things will be much better
Result 2: a Traitor
If one of our prisoners wants to get other help without offering any reward, he may be well benefited at first
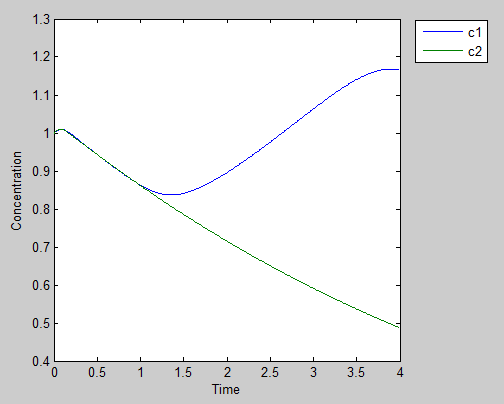
but as his partner gets into trouble, he will lose his luck. This though go against the realistic, we can also take well advantage of this flaw in our safety idea. (In the four cases of prisoners’ dilemma there are three cases that the bad man can escape but in our model only if they are well cooperate with each other then they will have chance to run away, but such a good cooperate cannot be easily achieved especially outside the Lab)
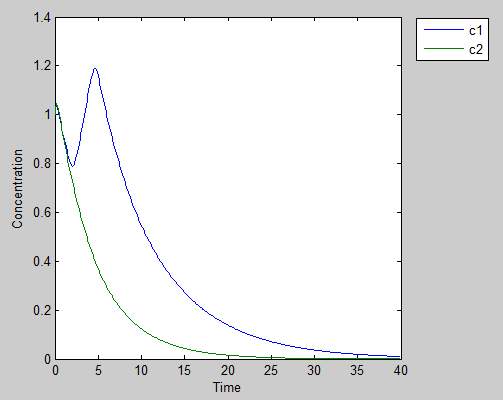
Result 3: The Egoists
If both guys are imaginary smart, and have a strong believe that his partner will forswear for him, it’s obvious that they will get deserved penalty.
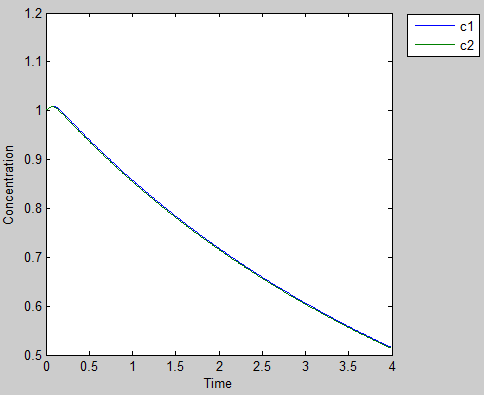
Some more interesting results
The results all above are just considering the same situation that both the prisoners have a similar personality, that says our two cells have a very symmetry structure, their physiological parameters are nearly the same. Basing on this, every cell can act the same behavior when meet the same change in the environment.
However, two pieces of leaves will never coincide in the world. We can’t adjust everything to meet our plan and this considerable material difference gives us the opportunity to have a sight of the real prisoner’s dilemma.
What will happen if we put two people with different sensibility of other’s goodwill into this dilemma? To achieve this, we can simply adjust the Hill coefficient of the differential equation of Zeor, to see what have found.
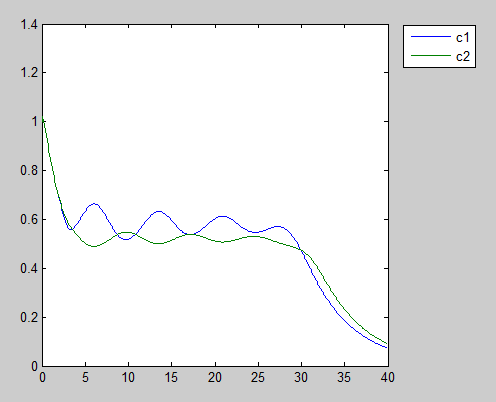
There appears a clear game between our prisoners, and unlike other results this dynamic equilibrium crashed at last. It’s usually a common sense that the damped oscillation may lead to a stable equilibrium, , but you can hardly tell which people made the mistake. How our prisoners can perform such clumsy play, maybe we can have a further study.
This media liked the whole modeling of our project.
Media:modelingsustc.pdf "
"