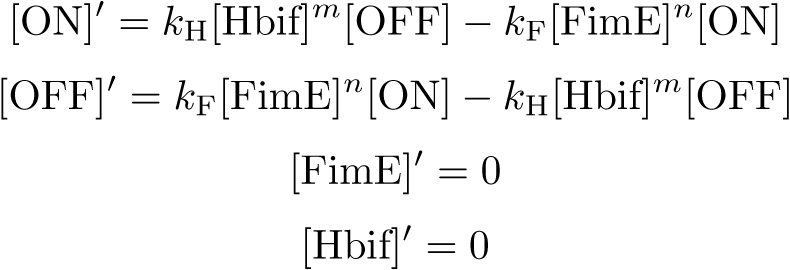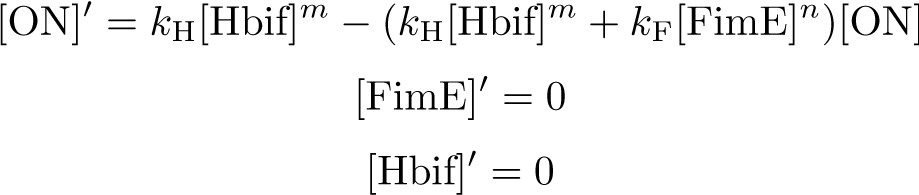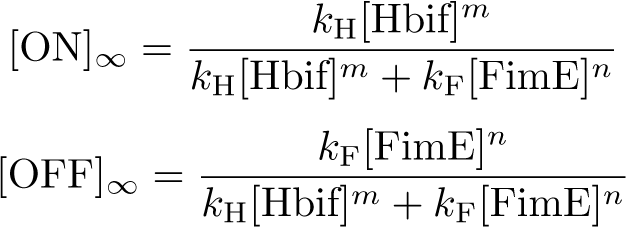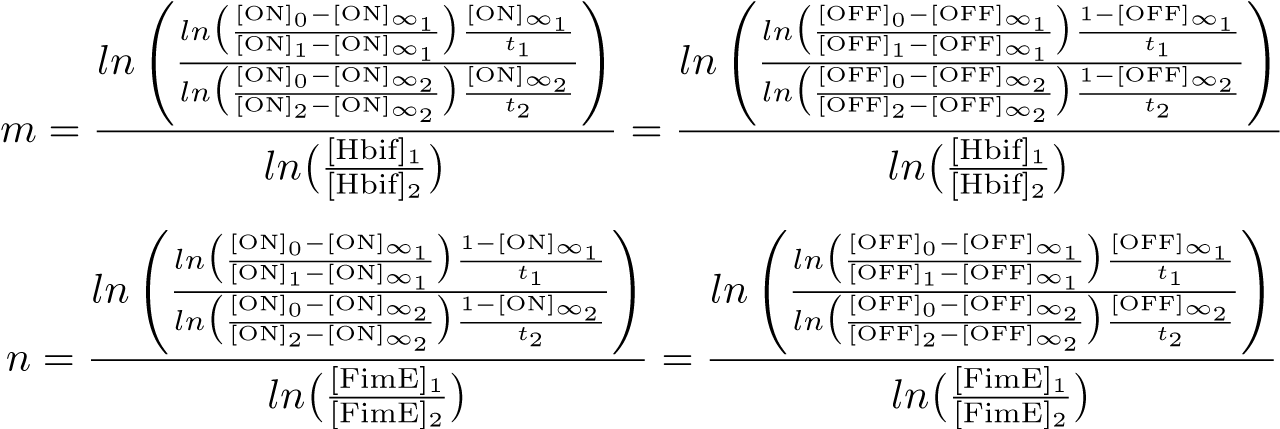Switch Model

From 2013.igem.org

(Difference between revisions)
(Replaced content with "{{:Team:Michigan_Template}} center center center center [[...")
 
(4 intermediate revisions not shown)
Line 10: Line 10:
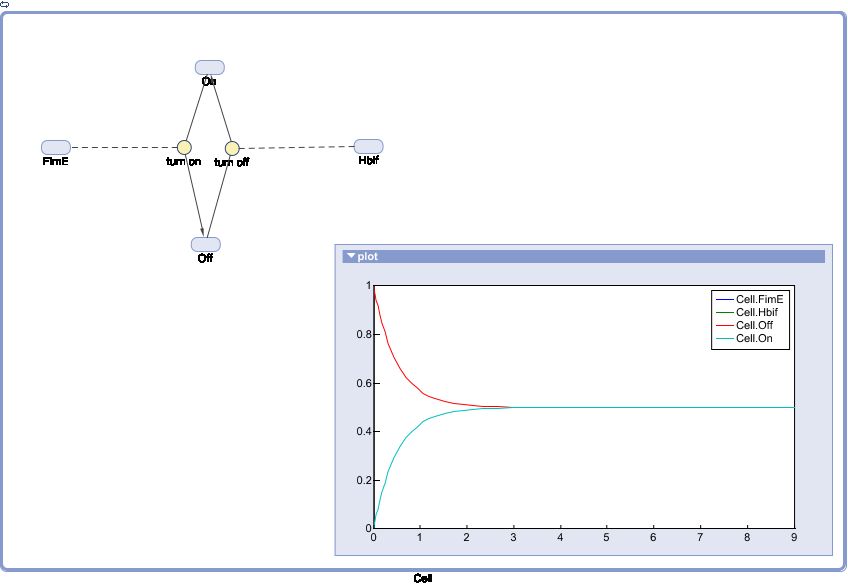
[[File:SwitchModel5-1.png|640px|center]]
[[File:SwitchModel5-1.png|640px|center]]
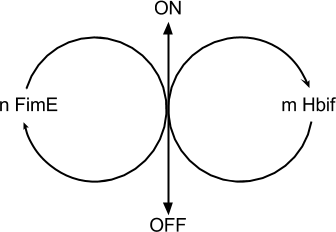
[[File:SwitchModel5-2.png|752px|center]]
[[File:SwitchModel5-2.png|752px|center]]
-
 
-
 
-
system:
 
-
\begin{equation*}
 
-
[\text{ON}]'=k_\text{H}[\text{Hbif}]^m[\text{OFF}]-k_\text{F}[\text{FimE}]^n[\text{ON}]
 
-
\end{equation*}
 
-
\begin{equation*}
 
-
[\text{OFF}]'=k_\text{F}[\text{FimE}]^n[\text{ON}]-k_\text{H}[\text{Hbif}]^m[\text{OFF}]
 
-
\end{equation*}
 
-
\begin{equation*}
 
-
[\text{FimE}]'=0
 
-
\end{equation*}
 
-
\begin{equation*}
 
-
[\text{Hbif}]'=0
 
-
\end{equation*}
 
-
conservation equation:
 
-
\begin{equation*}
 
-
[\text{ON}]+[\text{OFF}]=1
 
-
\end{equation*}
 
-
reduced model:
 
-
\begin{equation*}
 
-
[\text{ON}]'=k_\text{H}[\text{Hbif}]^m-(k_\text{H}[\text{Hbif}]^m+k_\text{F}[\text{FimE}]^n)[\text{ON}]
 
-
\end{equation*}
 
-
\begin{equation*}
 
-
[\text{FimE}]'=0
 
-
\end{equation*}
 
-
\begin{equation*}
 
-
[\text{Hbif}]'=0
 
-
\end{equation*}
 
-
steady state: \\
 
-
if $k_\text{H}[\text{Hbif}]^m+k_\text{F}[\text{FimE}]^n \neq 0$,
 
-
\begin{equation*}
 
-
[\text{ON}]_\infty=\frac{k_\text{H}[\text{Hbif}]^m}{k_\text{H}[\text{Hbif}]^m+k_\text{F}[\text{FimE}]^n}
 
-
\end{equation*}
 
-
\begin{equation*}
 
-
[\text{OFF}]_\infty=\frac{k_\text{F}[\text{FimE}]^n}{k_\text{H}[\text{Hbif}]^m+k_\text{F}[\text{FimE}]^n}
 
-
\end{equation*}
 
-
if $k_\text{H}[\text{Hbif}]^m=k_\text{F}[\text{FimE}]^n=0$,
 
-
\begin{equation*}
 
-
[\text{ON}]_\infty=[\text{ON}]_0
 
-
\end{equation*}
 
-
\begin{equation*}
 
-
[\text{OFF}]_\infty=1-[\text{ON}]_\infty=1-[\text{ON}]_0=[\text{OFF}]_0
 
-
\end{equation*}
 
-
calibration:
 
-
\begin{equation*}
 
-
m=\frac{ln\left(\frac{ ln\big(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_1}}{[\text{ON}]_1-[\text{ON}]_{\infty_1}}\big)\frac{[\text{ON}]_{\infty_1}}{t_1} }{ ln\big(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_2}}{[\text{ON}]_2-[\text{ON}]_{\infty_2}}\big)\frac{[\text{ON}]_{\infty_2}}{t_2} }\right)}{ln\big(\frac{[\text{Hbif}]_1}{[\text{Hbif}]_2}\big)} = \frac{ln\left(\frac{ ln\big(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_1}}{[\text{OFF}]_1-[\text{OFF}]_{\infty_1}}\big)\frac{1-[\text{OFF}]_{\infty_1}}{t_1} }{ ln\big(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_2}}{[\text{OFF}]_2-[\text{OFF}]_{\infty_2}}\big)\frac{1-[\text{OFF}]_{\infty_2}}{t_2} }\right)}{ln\big(\frac{[\text{Hbif}]_1}{[\text{Hbif}]_2}\big)}
 
-
\end{equation*}
 
-
\begin{equation*}
 
-
n=\frac{ln\left(\frac{ ln\big(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_1}}{[\text{ON}]_1-[\text{ON}]_{\infty_1}}\big)\frac{1-[\text{ON}]_{\infty_1}}{t_1} }{ ln\big(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_2}}{[\text{ON}]_2-[\text{ON}]_{\infty_2}}\big)\frac{1-[\text{ON}]_{\infty_2}}{t_2} }\right)}{ln\big(\frac{[\text{FimE}]_1}{[\text{FimE}]_2}\big)} = \frac{ln\left(\frac{ ln\big(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_1}}{[\text{OFF}]_1-[\text{OFF}]_{\infty_1}}\big)\frac{[\text{OFF}]_{\infty_1}}{t_1} }{ ln\big(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_2}}{[\text{OFF}]_2-[\text{OFF}]_{\infty_2}}\big)\frac{[\text{OFF}]_{\infty_2}}{t_2} }\right)}{ln\big(\frac{[\text{FimE}]_1}{[\text{FimE}]_2}\big)}
 
-
\end{equation*}
 
-
\begin{align*}
 
-
k_{H} &= \frac{1}{2}ln\big(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_1}}{[\text{ON}]_1-[\text{ON}]_{\infty_1}}\big)\frac{[\text{ON}]_{\infty_1}}{t_1}[\text{Hbif}]_1^{\frac{ln\left(\frac{ ln\big(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_1}}{[\text{ON}]_1-[\text{ON}]_{\infty_1}}\big)\frac{[\text{ON}]_{\infty_1}}{t_1} }{ ln\big(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_2}}{[\text{ON}]_2-[\text{ON}]_{\infty_2}}\big)\frac{[\text{ON}]_{\infty_2}}{t_2} }\right)}{ln(\frac{[\text{Hbif}]_1}{[\text{Hbif}]_2})}} \\
 
-
&\text{\phantom{nn}}+ \frac{1}{2}ln(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_2}}{[\text{ON}]_2-[\text{ON}]_{\infty_2}})\frac{[\text{ON}]_{\infty_2}}{t_2}[\text{Hbif}]_2^{\frac{ln\left(\frac{ ln\big(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_1}}{[\text{ON}]_1-[\text{ON}]_{\infty_1}}\big)\frac{[\text{ON}]_{\infty_1}}{t_1} }{ ln\big(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_2}}{[\text{ON}]_2-[\text{ON}]_{\infty_2}}\big)\frac{[\text{ON}]_{\infty_2}}{t_2} }\right)}{ln(\frac{[\text{Hbif}]_1}{[\text{Hbif}]_2})}} \\
 
-
&= \frac{1}{2}ln(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_1}}{[\text{OFF}]_1-[\text{OFF}]_{\infty_1}})\frac{1-[\text{OFF}]_{\infty_1}}{t_1}[\text{Hbif}]_1^{\frac{ln\left(\frac{ ln\big(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_1}}{[\text{OFF}]_1-[\text{OFF}]_{\infty_1}}\big)\frac{1-[\text{OFF}]_{\infty_1}}{t_1} }{ ln\big(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_2}}{[\text{OFF}]_2-[\text{OFF}]_{\infty_2}}\big)\frac{1-[\text{OFF}]_{\infty_2}}{t_2} }\right)}{ln(\frac{[\text{Hbif}]_1}{[\text{Hbif}]_2})}} \\
 
-
&\text{\phantom{nn}}+ \frac{1}{2}ln(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_2}}{[\text{OFF}]_2-[\text{OFF}]_{\infty_2}})\frac{1-[\text{OFF}]_{\infty_2}}{t_2}[\text{Hbif}]_2^{\frac{ln\left(\frac{ ln\big(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_1}}{[\text{OFF}]_1-[\text{OFF}]_{\infty_1}}\big)\frac{1-[\text{OFF}]_{\infty_1}}{t_1} }{ ln\big(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_2}}{[\text{OFF}]_2-[\text{OFF}]_{\infty_2}}\big)\frac{1-[\text{OFF}]_{\infty_2}}{t_2} }\right)}{ln(\frac{[\text{Hbif}]_1}{[\text{Hbif}]_2})}}
 
-
\end{align*}
 
-
\begin{align*}
 
-
k_{F} &= \frac{1}{2}ln(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_1}}{[\text{ON}]_1-[\text{ON}]_{\infty_1}})\frac{1-[\text{ON}]_{\infty_1}}{t_1}[\text{FimE}]_1^{\frac{ln\left(\frac{ ln\big(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_1}}{[\text{ON}]_1-[\text{ON}]_{\infty_1}}\big)\frac{1-[\text{ON}]_{\infty_1}}{t_1} }{ ln\big(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_2}}{[\text{ON}]_2-[\text{ON}]_{\infty_2}}\big)\frac{1-[\text{ON}]_{\infty_2}}{t_2} }\right)}{ln(\frac{[\text{FimE}]_1}{[\text{FimE}]_2})}} \\
 
-
&\text{\phantom{nn}}+ \frac{1}{2}ln(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_2}}{[\text{ON}]_2-[\text{ON}]_{\infty_2}})\frac{1-[\text{ON}]_{\infty_2}}{t_2}[\text{FimE}]_2^{\frac{ln\left(\frac{ ln\big(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_1}}{[\text{ON}]_1-[\text{ON}]_{\infty_1}}\big)\frac{1-[\text{ON}]_{\infty_1}}{t_1} }{ ln\big(\frac{[\text{ON}]_0-[\text{ON}]_{\infty_2}}{[\text{ON}]_2-[\text{ON}]_{\infty_2}}\big)\frac{1-[\text{ON}]_{\infty_2}}{t_2} }\right)}{ln(\frac{[\text{FimE}]_1}{[\text{FimE}]_2})}} \\
 
-
&= \frac{1}{2}ln(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_1}}{[\text{OFF}]_1-[\text{OFF}]_{\infty_1}})\frac{[\text{OFF}]_{\infty_1}}{t_1}[\text{FimE}]_1^{\frac{ln\left(\frac{ ln\big(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_1}}{[\text{OFF}]_1-[\text{OFF}]_{\infty_1}}\big)\frac{[\text{OFF}]_{\infty_1}}{t_1} }{ ln\big(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_2}}{[\text{OFF}]_2-[\text{OFF}]_{\infty_2}}\big)\frac{[\text{OFF}]_{\infty_2}}{t_2} }\right)}{ln(\frac{[\text{FimE}]_1}{[\text{FimE}]_2})}} \\
 
-
&\text{\phantom{nn}}+ \frac{1}{2}ln(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_2}}{[\text{OFF}]_2-[\text{OFF}]_{\infty_2}})\frac{[\text{OFF}]_{\infty_2}}{t_2}[\text{FimE}]_2^{\frac{ln\left(\frac{ ln\big(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_1}}{[\text{OFF}]_1-[\text{OFF}]_{\infty_1}}\big)\frac{[\text{OFF}]_{\infty_1}}{t_1} }{ ln\big(\frac{[\text{OFF}]_0-[\text{OFF}]_{\infty_2}}{[\text{OFF}]_2-[\text{OFF}]_{\infty_2}}\big)\frac{[\text{OFF}]_{\infty_2}}{t_2} }\right)}{ln(\frac{[\text{FimE}]_1}{[\text{FimE}]_2})}}
 
-
\end{align*}
 

Latest revision as of 22:16, 6 September 2013

Xayona Website Template

Switch.jpg
SwitchModelFigure.png
SwitchModel1.png
SwitchModel2.png
SwitchModel3.png
SwitchModel4-1.png
SwitchModel4-2.png
SwitchModel5-1.png
SwitchModel5-2.png
Retrieved from "http://2013.igem.org/Switch_Model"