Team:Alberta/Overview
From 2013.igem.org
| Line 449: | Line 449: | ||
<div class="sidebar"> | <div class="sidebar"> | ||
<div href class="tooltip"><img src="/wiki/images/7/7d/SideChar.png"></img> | <div href class="tooltip"><img src="/wiki/images/7/7d/SideChar.png"></img> | ||
| - | <span class="saying">Welcome to the Team Alberta Wiki! | + | <!--span class="saying">Welcome to the Team Alberta Wiki! |
<div id="box" style="width: 450px; padding: 5px; border: 3px solid #000; background-color: #000000;"> | <div id="box" style="width: 450px; padding: 5px; border: 3px solid #000; background-color: #000000;"> | ||
<div id="template" style="text-align: center; font-weight: bold; font-size: large; color: #f6f6f6; padding: 5px;"> | <div id="template" style="text-align: center; font-weight: bold; font-size: large; color: #f6f6f6; padding: 5px;"> | ||
| Line 455: | Line 455: | ||
</div> | </div> | ||
</div> | </div> | ||
| - | </span> | + | </span--> |
</div> | </div> | ||
</div> | </div> | ||
Revision as of 02:57, 28 September 2013
Overview
The Travelling Salesman Problem
The Littlest Mapmaker is Team Alberta's endeavour to create a biological computer capable of solving Travelling Salesman Problems (TSP), a general form of problem that asks:
Given a set of cities, and a list of the distances between each pair of those cities, what is the shortest possible route that travels to every city exactly once and then returns to the origin city?
In Biological Terms
To solve a TSP biologically, we must create biochemical analogues for all of the components of the original problem. For the Littlest MapMaker, we do this by assigning a symbolic bacterial reporter gene or selectable marker gene to each of the paths that connect a pair of cities. For instance, for the example map featured here, the path connecting cities A and B is symbolized by a gene coding for ampicillin antibiotic resistance. This allows us to describe routes through the network as a sequence of genes, standing for a sequence of paths. Again for example, the route travelling from city A to B, then to C, and then to D before returning to A is described by the sequence ampicillin resistance gene, followed by green fluorescent protein gene, then blue amyl chromoprotein gene, and finally chloramphenicol resistance gene.
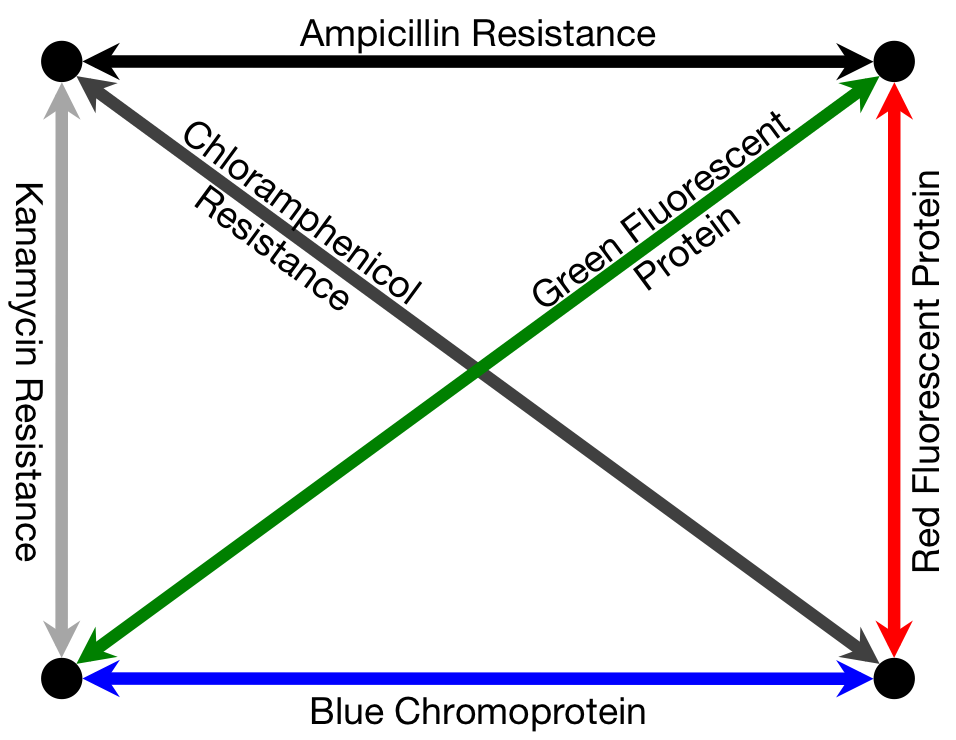
Finding the Path
Our biocomputer tests the different routes by assembling plasmids with the corresponding gene sequences. All of the various possible plasmids are assembled simultaneously, through a series of biased ligation reactions that prefer assembly of plasmids that use short paths — that is, those genes that symbolize shorter paths are more likely to be incorporated into a plasmid than those which symbolize longer paths (see “Building the Routes” below for more detail on how we create this preference). Billions of plasmids are produced in this way, and because of the bias in favour of short path genes, the predominating products are gene sequences that correspond to very short routes. Identifying the predominant product of the assembly would, in turn, identify the shortest path and therefore the solution to the problem.
MapMakers at Work
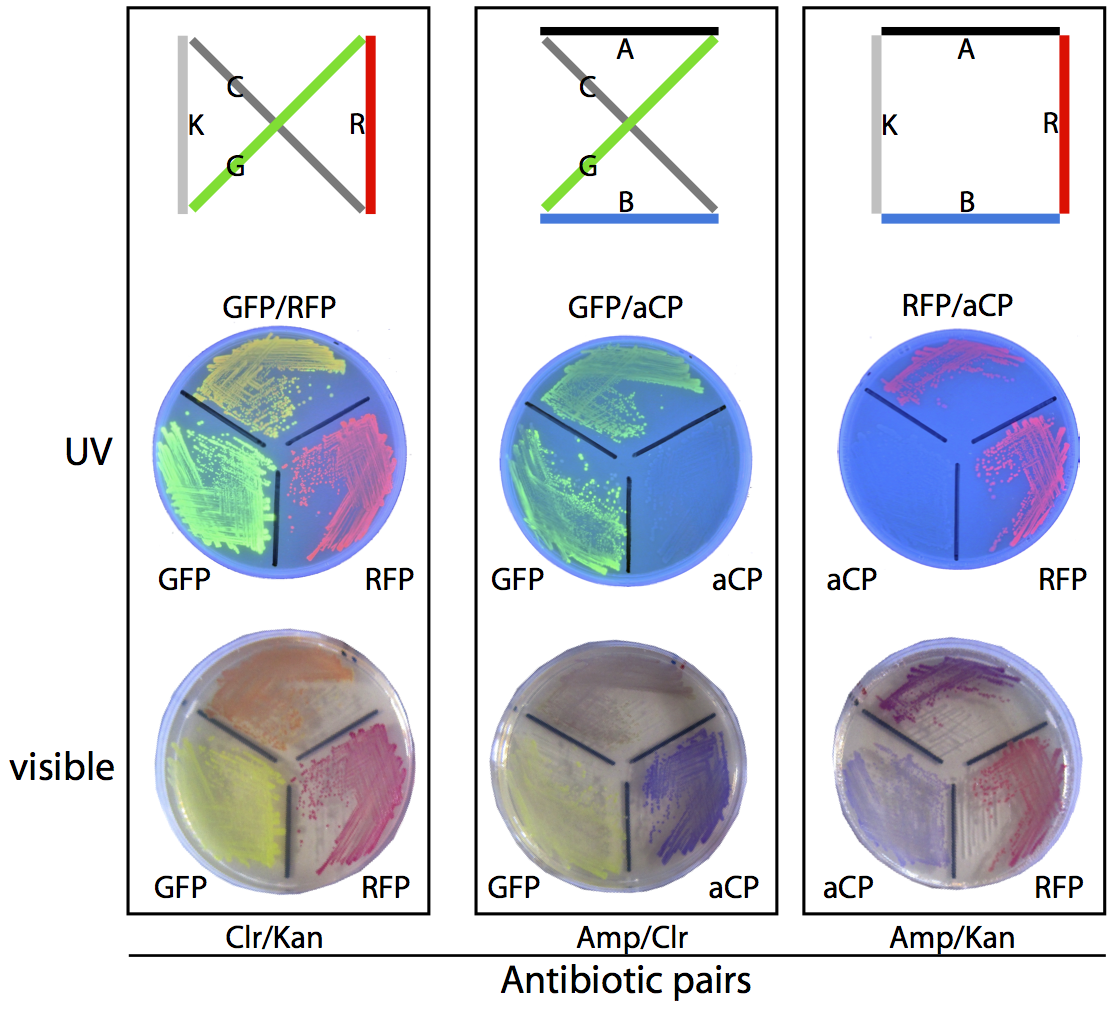
Unfortunately, as a byproduct of our assembly method, many of the plasmids generated this way do not correspond to any valid route through the assigned set of cities, and these need to be filtered out so that the frequency of production of each of the valid routes can be compared. To compute the validity of the plasmids, we transform them into a culture of E. coli, which are then grown on antibiotic-treated plates and allowed to express their reporter genes, making it simple to unambiguously identify the plasmid employed by a given colony based on its colouration and resistances.
For example, consider the three possible routes for our sample four-city problem. The solution shown at the right of the diagram below produces colonies that are coloured purple (a combination of the blue chromoprotein and red fluorescent protein reporter genes) and is able to survive on ampicillin/kanamycin plates. This is the only combination of genes that will result in this combination of colour and resistances. To determine which of the three routes is the solution to this travelling salesman problem, we plate the bacterial culture across these antibiotic plates and count the colonies that match with the three valid routes. The most commonly occurring bacterial genotype will correspond to the optimal route.
Building the Routes
Our plasmid assembly system relies upon the achievements of previous Team Alberta iGEM entries, 2009’s BioBytes and 2010’s Genomikon assembly methods, which are noteworthy for their ability to assemble our 5000bp, four-gene plasmid in an afternoon. In this method, plasmid origins of replication are anchored to magnetic beads and left with a single, free-floating sticky end, onto which a new gene with the corresponding sticky end is ligated. The free sticky end of the newly ligated gene is not able to interact with anything in the solution at this time, ensuring that there are no unwanted by-products. After this ligation reaction, the magnetic beads are used to extract the product strands, washing away any non-anchored DNA and enzyme.

Applying Magnetic Bead Assembly to the TSP Problem
The second ligation adds a short, 25-base-pair linker strand to the free end, which replaces the free sticky end with one that is able to receive another gene, allowing (after another wash) for the next gene to be ligated onto the growing strand.
Once all of the genes have been ligated (alternating with linkers), a tail-piece that complements the original bead-anchor DNA sequence is added, so that the finished product can be unbound from the beads and will close upon itself to form the circular plasmid. In this fashion, a four-gene, roughly 5000-base-pair plasmid is assembled in as little as an afternoon, cheaply and easily.
When we ligate a new gene to the growing strand in this process, we provide the reaction with several genes, representing every path that the travelling salesman problem might take at that step. We bias the system to favour short paths by setting the concentration of the added genes based on the reciprocal of the corresponding path’s length, as adjusted by a calibration coefficient (C in the formula below). As a result, a gene that symbolizes a short path will be included in the reaction at higher concentration than a gene that symbolizes a long path, and the shorter path genes will occur more frequently among the product plasmids.

For example, if the path corresponding to the ampicillin resistance gene in a particular TSP takes only one unit of distance, while the chloramphenicol resistance gene path in the same problem takes four units of distance, then we might use 0.4 picomoles of the AmpR gene, and 0.1 picomoles of the ChlorR gene when adding those two genes to the ligation. We would then expect the ratio of products to be roughly 4:1 AmpR to ChlorR, favouring the shortest path more in proportion to its distance.
Calibration for Error
Since the actual output for the Littlest MapMaker is determined by a number of biological factors, including transformation efficiency, antibiotic toxicity, strain from reporter gene production, and more, the number of colonies that result from a given assembly of DNA is not a direct result of the relative proportions of plasmids produced. To compensate for these factors, we calibrated our computer through trial runs, which provides us with a calibration coefficient. As an example, we found that even if equal concentrations of the aCP (blue chromoprotein) and GFP (green fluorescent protein) genes are used to assemble plasmids, roughly six colonies will grow expressing aCP for every one expressing GFP. As a result, we calibrate in favour of GFP, adjusting the target concentration of all instances of GFP upward by six times, which compensates for the bias. A trial with these same values resulted in a more even expression of the two genes from among the resulting colonies.
We expect that as the system is used to solve more complex problems, this simple method of calibration will be insufficient, requiring further testing to characterize the mathematical relationship between gene concentration in ligations and the frequency of that gene among the resulting colonies.
 "
"






