Team:TU-Munich/Modeling/Kill Switch
From 2013.igem.org
ChristopherW (Talk | contribs) (→siRNA Model) |
ChristopherW (Talk | contribs) (→siRNA Model) |
||
| Line 20: | Line 20: | ||
We determined the governing equations of this model to be the following: | We determined the governing equations of this model to be the following: | ||
| - | [[File:TUM13_siRNA_formula.png]] | + | [[File:TUM13_siRNA_formula.png|center]] |
| + | with initial conditions V(0) = 1 and R(0) = 0, where at the time t=0 the trigger is activated. | ||
| + | The stable points V* and R* of this system have to satisfy. | ||
[[File:TUM13_siRNA_stable_satisfy.png|center]] | [[File:TUM13_siRNA_stable_satisfy.png|center]] | ||
| - | Defining [[File:TUM13_siRNA_alpha_beta_def.png]] | + | Defining [[File:TUM13_siRNA_alpha_beta_def.png]] we get the following quadratic equation for the stable point of V |
| - | + | ||
| - | + | ||
[[File:TUM13_siRNA_stable_quadratic.png|center]] | [[File:TUM13_siRNA_stable_quadratic.png|center]] | ||
| - | [[File:TUM13_siRNA_alpha_eq_1.png | + | If [[File:TUM13_siRNA_alpha_eq_1.png]], the unique stable point is [[File:TUM13_siRNA_alphaIS1_stable.png]]. To analyze the stability of these the eigenvalues of the Hessian matrix H |
| - | + | ||
| - | [[File:TUM13_siRNA_alphaIS1_stable.png | + | |
| - | + | ||
[[File:TUM13_siRNA_alphaIS1_Hessian.png|center]] | [[File:TUM13_siRNA_alphaIS1_Hessian.png|center]] | ||
| - | + | must be computed. The eigenvalues are [[File:TUM13_siRNA_alphaIS1_EV.png]]. | |
| - | [[File:TUM13_siRNA_alphaIS1_EV.png | + | |
[[File:TUM13_siRNA_alpha_neq_1.png|center]] | [[File:TUM13_siRNA_alpha_neq_1.png|center]] | ||
Revision as of 14:24, 3 October 2013
Kill Switch Modeling
Purpose
The idea of our kill switch is to kill off our moss, as soon as it leaves the filter system. For this purpose two methods were proposed:
- siRNA method: When some trigger is activated, siRNA is expressed inhibiting the expression of a vital gene
- nuclease method: When some trigger is activated, a nuclease is released destroying the DNA of the cell
To decide between these two methods we modelled the vitality V of the cell (a number between 0 and 1, so a perfectly functional cell has V=1, a dead cell V=0) and depending on the tested method the concentration of siRNA R and nuclease N as appropriate. Both concentrations are normalized to the unit interval [0,1].
siRNA Model
We determined the governing equations of this model to be the following:
with initial conditions V(0) = 1 and R(0) = 0, where at the time t=0 the trigger is activated.
The stable points V* and R* of this system have to satisfy.
Defining ![]() we get the following quadratic equation for the stable point of V
we get the following quadratic equation for the stable point of V
If ![]() , the unique stable point is
, the unique stable point is ![]() . To analyze the stability of these the eigenvalues of the Hessian matrix H
. To analyze the stability of these the eigenvalues of the Hessian matrix H
must be computed. The eigenvalues are ![]() .
.
Nuclease Modell
Conclusion
For a functional kill-switch it is necessary, that the cells are actually killed completely and not just live on with reduced vitality. So based on our modelling results the siRNA approach is not satisfactory, while the nuclease satisfies the requirement. As a result the team pursued the nuclease approach leading to our final kill-switch.
 "
"



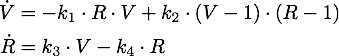
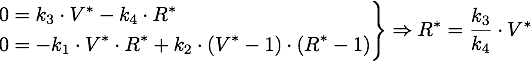
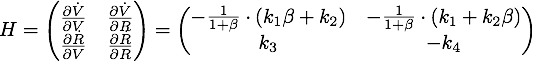
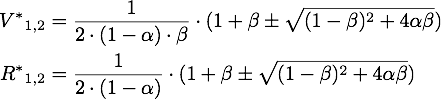
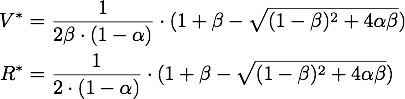
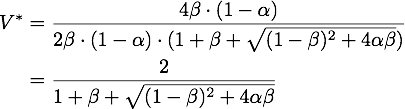
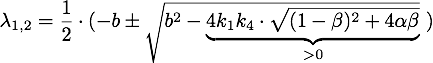
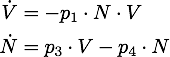

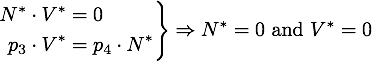
AutoAnnotator:
Follow us:
Address:
iGEM Team TU-Munich
Emil-Erlenmeyer-Forum 5
85354 Freising, Germany
Email: igem@wzw.tum.de
Phone: +49 8161 71-4351