Team:Newcastle/Project/shape shifting
From 2013.igem.org
(→Our Project) |
|||
| (75 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
{{Team:Newcastle}} | {{Team:Newcastle}} | ||
| - | =Shape | + | =Shape Shifting= |
| - | + | Most bacteria have evolved to have a cell wall, and those which do not, have cell walled ancestry [https://2013.igem.org/Team:Newcastle/Project/shape_shifting#References (Trachtenberg 1998, Errington 2013)]. The cell wall is a rigid structure which protects the bacteria from the variety of environmental hazards such as mechanical stress, osmotic rupture and lysis. The cell wall often serves as a docking point to many proteins including various receptors and adherence sites. In addition to these features, the cell wall provides the cell with a rigid boundary and helps bacteria to acquire and preserve their shape. In ''Bacillus subtilis'' a group of proteins termed Penicillin Binding Proteins (Pbp), along with other proteins, usually anchored in the cell wall, are involved in the formation of the rod shape. When the cells lose their cell wall they automatically lose these proteins to the environment as they are being made. The cells lose their support and become spherical in shape - this is the most energetically favourable state (ratio of surface area to volume is minimal, and membrane curvature is more-or-less constant). | |
| - | == | + | ===The idea=== |
| - | + | ||
| - | + | [http://www.ncbi.nlm.nih.gov/pubmed/10049810 It has been previously observed] that these cell wall-less bacteria can become elongated and 'squeeze' into spaces with a smaller diameter than theirs. This fact sparked our interest and led us to ask some questions. L-forms are an improved secretory machine; the cell wall hinders excretion of some proteins. Could L-forms be used as a delivery vehicle in small or out-of-reach areas? Such hard-to-reach areas include intercellular spaces and micro-cracks in solid materials, which are smaller than 1 μm. ''B.subtilis'' in L-form state, can grow to large sizes before they divide. Is it possible to fill spaces of various shapes and sizes with L-forms? | |
| - | + | ||
| - | + | To research into these areas, we intended to manipulate L-forms using microfluidics. Microfluidics allows manipulation of single cells via precise movement of fluids in the micro scale. Microfluidic chips were designed on autoCAD which were to be used to produce silicon wafer master moulds. Unfortunately these were not created in time. | |
| - | + | ||
| - | + | [[File:Microfluidics_set_up.jpg|400px]] | |
| + | ''Figure 1. The set up for microfluidics to visualise individual L-forms'' | ||
| - | + | The idea was to use directed flow within the microfluidic wafer to physically manoeuvre L-form cells into designed chambers of different shapes, such as those shown in Figure 2. The membranes of the L-forms were to be stained with FM.595 and through this staining we would be able to visualise whether the L-forms were able to adopt the different shapes within the microfluidic wafer. | |
| + | |||
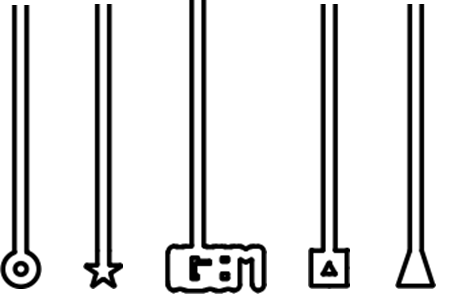
| + | [[File:Microfluidics_chambers.png|400px]] | ||
| - | + | ''Figure 2. The design of the chambers which L-forms would be forced into. The L-forms would potentially adopt the shape of the terminal part of the chambers.'' | |
| - | === | + | ===Modelling=== |
| - | + | ||
| - | === | + | To show the flexibility of L-forms we planned to trap them in microfluidics chambers whose shape differs from that of a normal L-form e.g. a star, square or triangle shape. |
| + | |||
| + | Before we began to design the experiments, we wished to illustrate the process which we predict to occur inside of the terminal chamber as the cell grows. For this, we constructed a model of the predicted cell behaviour as it grows inside a square. This model was based on the knowledge that we have about the processes inside the cell which are involved in membrane synthesis and growth. We would like to thank Dr. David Swailes from the School of Mechanical Engineering at Newcastle University for the great amount of help with the mathematical aspects of this modelling. | ||
| + | |||
| + | For the purposes of this study, the complexity of a growing cell inside a confined space can be broken down to simpler models of the system at two phases. The first phase is a constantly growing cell, this phase is followed by the cell gradually adopting the shape of the boundaries. | ||
| + | |||
| + | The full description of the model can be found on this [https://2013.igem.org/Team:Newcastle/Modelling/CellShapeModel page]. | ||
| + | |||
| + | This model can be improved by conducting experiments which would allow us to find accurate parameters such as the rate of membrane synthesis and maximum membrane torsion. Freeing the model of a few assumptions would also be beneficial. For example if the effects of nutrient depletion were found, and if the maximum size the cell could grow to before dividing was derived, then these could be worked into the model. The model could also be expanded in terms of factoring in the bending energy of the membrane in a particular shape. This would allow us to compare the models of the cells adopting different shapes and to evaluate which shape would me more readily assumed. It would also be interesting to see whether the state of the cell (i.e. L- or rod form) before it enters the chamber has any bearing on the way it fills the space. The page devoted to [https://2013.igem.org/Team:Newcastle/Modelling/CellShapeModel this model can be found here], we invite you to have a look at it and try to run it yourself (the MATLAB code is all right there). | ||
| + | |||
| + | |||
| + | ===References=== | ||
| + | [http://www.ncbi.nlm.nih.gov/pubmed/10049810 Trachtenberg S. (1998) Mollicutes-wall-less bacteria with internal cytoskeletons. ''Journal of Structural Biology''. '''124''', 244-256.] | ||
| + | |||
| + | [http://www.ncbi.nlm.nih.gov/pubmed/23303308 Errington J. (2013) L-form bacteria, cell walls and the origins of life. ''Open Biology'', '''3''', 120143] | ||
| + | |||
| + | {{Template:Team:Newcastle/Sponsors}} | ||
Latest revision as of 18:44, 28 October 2013

Contents |
Shape Shifting
Most bacteria have evolved to have a cell wall, and those which do not, have cell walled ancestry (Trachtenberg 1998, Errington 2013). The cell wall is a rigid structure which protects the bacteria from the variety of environmental hazards such as mechanical stress, osmotic rupture and lysis. The cell wall often serves as a docking point to many proteins including various receptors and adherence sites. In addition to these features, the cell wall provides the cell with a rigid boundary and helps bacteria to acquire and preserve their shape. In Bacillus subtilis a group of proteins termed Penicillin Binding Proteins (Pbp), along with other proteins, usually anchored in the cell wall, are involved in the formation of the rod shape. When the cells lose their cell wall they automatically lose these proteins to the environment as they are being made. The cells lose their support and become spherical in shape - this is the most energetically favourable state (ratio of surface area to volume is minimal, and membrane curvature is more-or-less constant).
The idea
[http://www.ncbi.nlm.nih.gov/pubmed/10049810 It has been previously observed] that these cell wall-less bacteria can become elongated and 'squeeze' into spaces with a smaller diameter than theirs. This fact sparked our interest and led us to ask some questions. L-forms are an improved secretory machine; the cell wall hinders excretion of some proteins. Could L-forms be used as a delivery vehicle in small or out-of-reach areas? Such hard-to-reach areas include intercellular spaces and micro-cracks in solid materials, which are smaller than 1 μm. B.subtilis in L-form state, can grow to large sizes before they divide. Is it possible to fill spaces of various shapes and sizes with L-forms?
To research into these areas, we intended to manipulate L-forms using microfluidics. Microfluidics allows manipulation of single cells via precise movement of fluids in the micro scale. Microfluidic chips were designed on autoCAD which were to be used to produce silicon wafer master moulds. Unfortunately these were not created in time.
Figure 1. The set up for microfluidics to visualise individual L-forms
The idea was to use directed flow within the microfluidic wafer to physically manoeuvre L-form cells into designed chambers of different shapes, such as those shown in Figure 2. The membranes of the L-forms were to be stained with FM.595 and through this staining we would be able to visualise whether the L-forms were able to adopt the different shapes within the microfluidic wafer.
Figure 2. The design of the chambers which L-forms would be forced into. The L-forms would potentially adopt the shape of the terminal part of the chambers.
Modelling
To show the flexibility of L-forms we planned to trap them in microfluidics chambers whose shape differs from that of a normal L-form e.g. a star, square or triangle shape.
Before we began to design the experiments, we wished to illustrate the process which we predict to occur inside of the terminal chamber as the cell grows. For this, we constructed a model of the predicted cell behaviour as it grows inside a square. This model was based on the knowledge that we have about the processes inside the cell which are involved in membrane synthesis and growth. We would like to thank Dr. David Swailes from the School of Mechanical Engineering at Newcastle University for the great amount of help with the mathematical aspects of this modelling.
For the purposes of this study, the complexity of a growing cell inside a confined space can be broken down to simpler models of the system at two phases. The first phase is a constantly growing cell, this phase is followed by the cell gradually adopting the shape of the boundaries.
The full description of the model can be found on this page.
This model can be improved by conducting experiments which would allow us to find accurate parameters such as the rate of membrane synthesis and maximum membrane torsion. Freeing the model of a few assumptions would also be beneficial. For example if the effects of nutrient depletion were found, and if the maximum size the cell could grow to before dividing was derived, then these could be worked into the model. The model could also be expanded in terms of factoring in the bending energy of the membrane in a particular shape. This would allow us to compare the models of the cells adopting different shapes and to evaluate which shape would me more readily assumed. It would also be interesting to see whether the state of the cell (i.e. L- or rod form) before it enters the chamber has any bearing on the way it fills the space. The page devoted to this model can be found here, we invite you to have a look at it and try to run it yourself (the MATLAB code is all right there).
References
[http://www.ncbi.nlm.nih.gov/pubmed/10049810 Trachtenberg S. (1998) Mollicutes-wall-less bacteria with internal cytoskeletons. Journal of Structural Biology. 124, 244-256.]
[http://www.ncbi.nlm.nih.gov/pubmed/23303308 Errington J. (2013) L-form bacteria, cell walls and the origins of life. Open Biology, 3, 120143]
 "
"