Team:Alberta
From 2013.igem.org
(→) |
(→) |
||
| Line 11: | Line 11: | ||
| - | <html><p><font size= | + | <html><p><font size=4><strong><center> |
Team Alberta represents the University of Alberta, from Edmonton</p> | Team Alberta represents the University of Alberta, from Edmonton</p> | ||
| Line 17: | Line 17: | ||
[[Image:Alberta_logo.png|300px|center]] | [[Image:Alberta_logo.png|300px|center]] | ||
| - | <html><font size= | + | <html><font size=3>The traveling salesman problem is a mathematical optimization problem that was first formally described in 1930, and has been intensively studied in the computer sciences as a benchmark for optimization algorithms. The problem asks: |
In our project, we use DNA to compute solutions by converting all of the elements of the problem into representative sequences of DNA: cities become selectable marker genes (specifically, antibiotic resistance genes), paths between the cities become short, sticky-ended linkers (each of which is only able to ligate to two specific “city” strands), and the distance of a given path is represented by the concentration of the corresponding linker in solution. These pieces of DNA are successively ligated together to produce plasmids that act as “maps”, where the order in which the genes appear in the plasmid describes a route travelling to the various cities in the problem. </font></html> | In our project, we use DNA to compute solutions by converting all of the elements of the problem into representative sequences of DNA: cities become selectable marker genes (specifically, antibiotic resistance genes), paths between the cities become short, sticky-ended linkers (each of which is only able to ligate to two specific “city” strands), and the distance of a given path is represented by the concentration of the corresponding linker in solution. These pieces of DNA are successively ligated together to produce plasmids that act as “maps”, where the order in which the genes appear in the plasmid describes a route travelling to the various cities in the problem. </font></html> | ||
| Line 23: | Line 23: | ||
|[[Image:sample_product.png|300px]][[Image:sample_route.png|600px]] | |[[Image:sample_product.png|300px]][[Image:sample_route.png|600px]] | ||
|} | |} | ||
| - | <html><font size= | + | <html><font size=3>The resulting plasmids are transformed into a bacterial culture, so that we can select for only those plasmids that include every city in the list. Then, plasmid DNA is extracted from the surviving bacterial colonies and analyzed to determine which plasmid (and thus which route) occurred the most frequently. This route, the one most favoured by the ligation reactions, is the optimal route!</font></html> |
{| style="color:#1b2c8a;background-color:#0c6;" cellpadding="3" cellspacing="1" border="1" bordercolor="#fff" width="62%" align="center" | {| style="color:#1b2c8a;background-color:#0c6;" cellpadding="3" cellspacing="1" border="1" bordercolor="#fff" width="62%" align="center" | ||
Revision as of 18:47, 8 August 2013
Our project is called "The Littlest Mapmakers", an attempt to create a biological computer capable of solving the Traveling Salesman Problem
The traveling salesman problem is a mathematical optimization problem that was first formally described in 1930, and has been intensively studied in the computer sciences as a benchmark for optimization algorithms. The problem asks: In our project, we use DNA to compute solutions by converting all of the elements of the problem into representative sequences of DNA: cities become selectable marker genes (specifically, antibiotic resistance genes), paths between the cities become short, sticky-ended linkers (each of which is only able to ligate to two specific “city” strands), and the distance of a given path is represented by the concentration of the corresponding linker in solution. These pieces of DNA are successively ligated together to produce plasmids that act as “maps”, where the order in which the genes appear in the plasmid describes a route travelling to the various cities in the problem.
 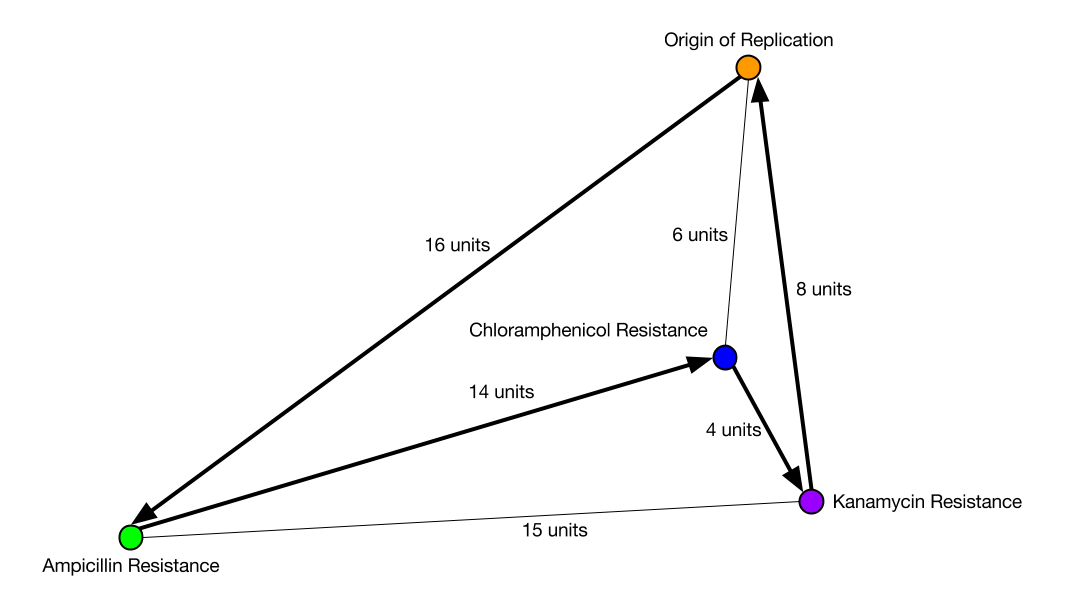
|
The resulting plasmids are transformed into a bacterial culture, so that we can select for only those plasmids that include every city in the list. Then, plasmid DNA is extracted from the surviving bacterial colonies and analyzed to determine which plasmid (and thus which route) occurred the most frequently. This route, the one most favoured by the ligation reactions, is the optimal route!
| Home | Team | Official Team Profile | Project | Parts Submitted to the Registry | Modeling | Notebook | Safety | Attributions |
|---|
 "
"
