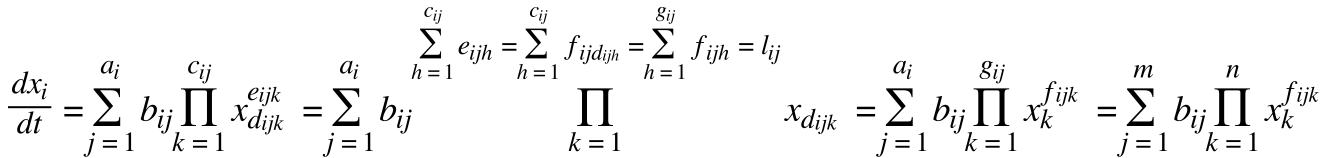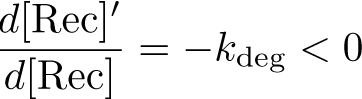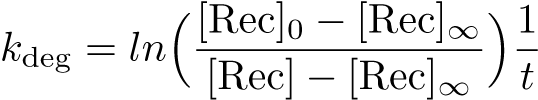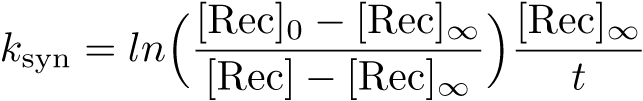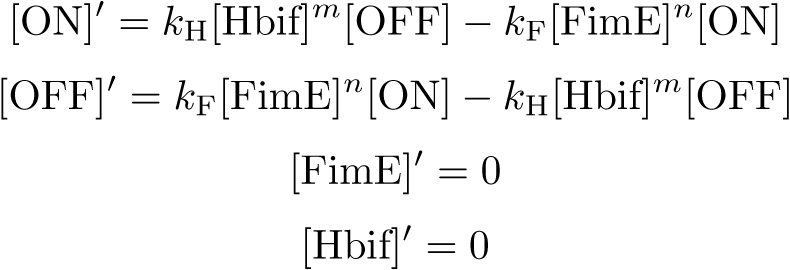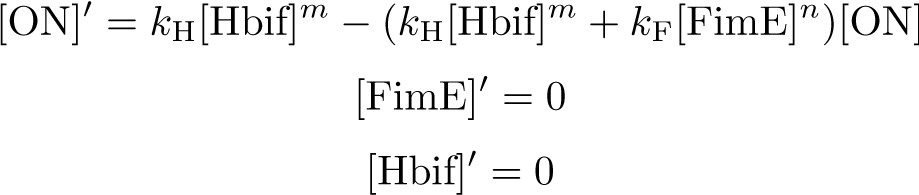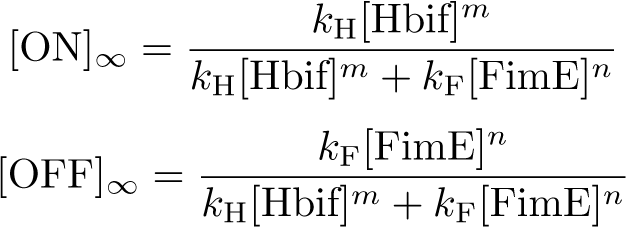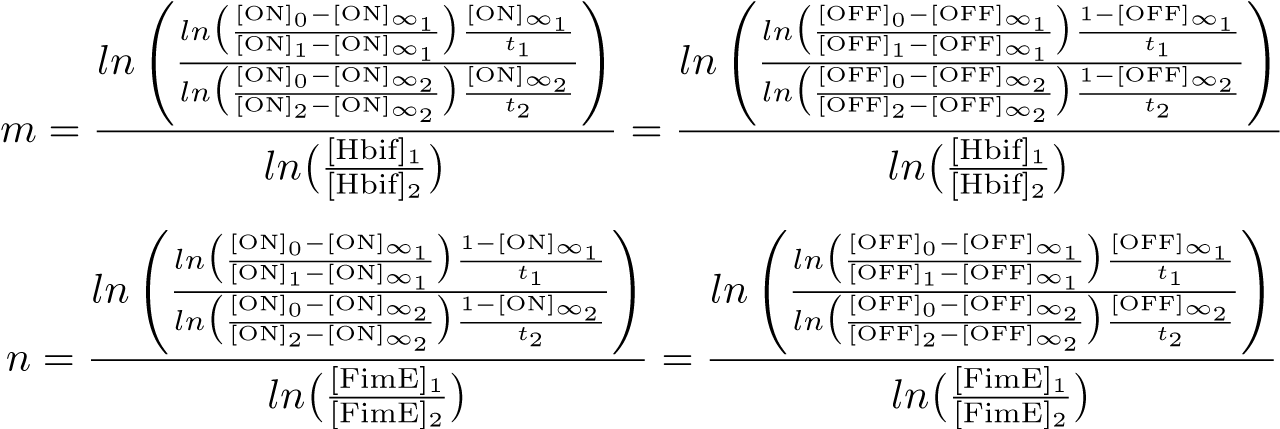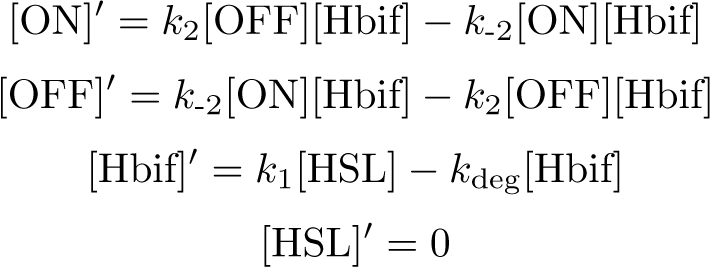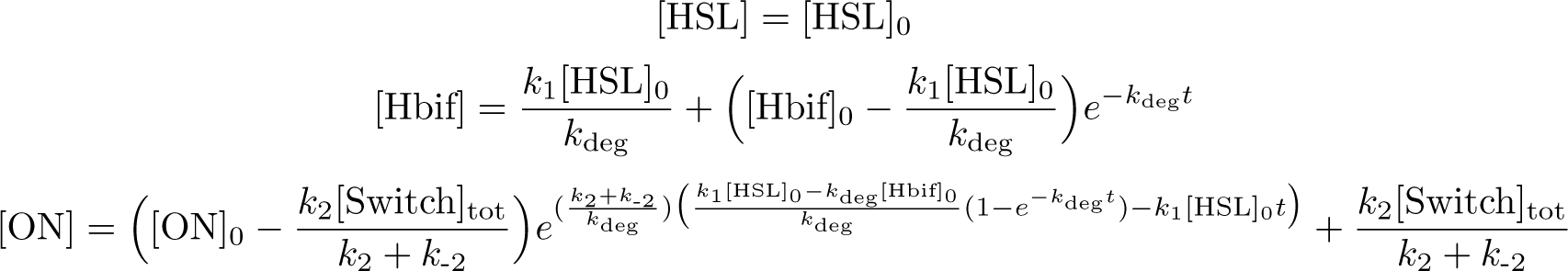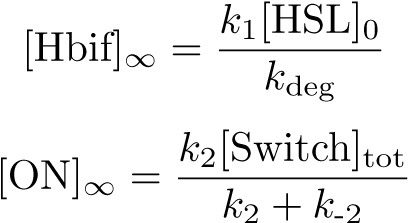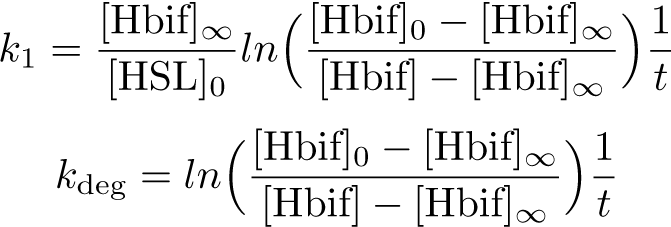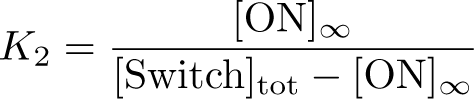From 2013.igem.org

(Difference between revisions)

Latest revision as of 23:58, 18 October 2013

Xayona Website Template

Introduction

Switch modeling

The goal for our modeling was to create rigorous standard procedures for mathematically representing and analyzing systems. Using our project as an example, we worked to demonstrate the viability of our approach by calculating the switch positions and optimum parameters. This standardization should be useful in combination with system specific methods to create better modeling.

Mass action modeling

Mass action is a form of modeling that uses systems of homogenous differential and difference equations. Each equation is a sum of rates and each rate is proportional to the species involved. The advantage is its straightforward uniform formulation, its minimal assumptions, and its flexibility of complexity. Mass action itself uses very few assumptions but it can be used to represent systems of varying degrees of simplicity. The fundamentals of chemical kinetics already champion the use of this modeling in its use of rate equations. There chemical systems are completely defined by the products, reactants, and reaction rate constants. This allows chemical modelling to be highly standardized and hence more accessible. It's actually the uniform nature of mass action that's responsible. Most importantly for iGEM, all mass action models can actually be put in a standard form as follows:

• x is a species

• a is an amount of rates changing x

• b is a rate constant

• c is a number of different species involved

• d is a species involved

• e is a number of each species involved

• f is a number of species d involved

• g is a highest species involved

• l is a rate order

• m is the highest number of rates involved

• n is the number of species

Analytical modeling

Benefits

Given the parameters of the system, analytical (symbolic) modeling precisely predicts a system's behavior. Furthermore, unlike numerical methods, analytical modeling accurately predicts the data needed to determine parameters and avoids the inherent numerical rounding and approximation errors of more crude analyses. Analytical modeling naturally lends itself to standardization because the results are unique to any given model. Correct solutions, equilibria, eigenvalues, etc. will always have the same expression regardless of who or what calculated them. The same can't be said for numerical methods. With this and the iGEM community in mind, an analytical standard was developed that will allow for the exchange and automation of future modeling.

ERSESCO Algorithm

The ERSESCO algorithm the Michigan team developed provides a clearly defined method for analyzing mathematical systems. The algorithm has seven major steps:

1. Equation: Formulate the system into a system of differential equations.

2. Reduction: Apply constraints, boundary conditions, and conservation laws to reduce the system of equations to fewer variables.

3. Solution: Solve the reduced system of equations, if possible.

4. Equilibration: Find the steady states of the system by setting differential equations to zero and solving for critical points.

5. Stabilization: Evaluate the Jacobian matrix of the system of equations at each critical point and find the corresponding eigenvalues. To get stability, find the condition for which all eigenvalues have a negative real part.

6. Calibration: Solve for the parameters of the system of equations in terms of the system's initial, steady state, time-dependent variables. This step allows the system parameters to be easily characterized using experimental data.

7. Optimization: Optimize the steady state, eigenvalues, parameters, or other desired quantity by equating the derivative of that quantity with respect to each of the system's parameters with zero. Solving these equations gives the optimization conditions for that quantity.

SimBiology

SimBiology is a useful MATLAB package provided to all iGEM teams. It can be used as a tool to quickly run numerical approximations of biological systems whether or not data for system parameters are known. SimBiology can quickly produce a model from a simple schematic diagram. As a result, the package can quickly provide a qualitative analysis of a system with little work from the user.

In the following models, our team applied our ERSESCO algorithm to fully analyze the systems at hand. Finally a SimBiology simulation was used as qualitative verification. We present the results from each step of the ERSESCO algorithm, followed by a SimBiology schematic with a graph showing the general behavior of the system, followed by a link to a more detailed derivation of the models.

Expression Model

The Recombinase Expression Model describes the synthesis and degradation of any protein produced at a relatively constant rate. Here, the model is used in particular to describe the synthesis and degradation reaction rates ksyn and kdeg of recombinases in the cell. The model also predicts the recombinase concentration.

Equation:

Reduction: None

Solution:

Equilibration:

Stabilization:

Calibration:

Optimization:

SimBiology:

Derivation: Expression Model

Switch Model

The Switch Model describes how the switch equilibrates when the concentrations of the recombinases FimE and Hbif approach constant values. The model assumes that each recombinase catalyzes a one way reaction. This model predicts the degree of cooperativity n and m in the binding reaction of the recombinase to DNA for FimE and Hbif, respectively. Furthermore, this model predicts the forward catalysis rate constants, kF and kH, for FimE and Hbif.

Equation:

Reduction:

Solution:

Equilibration:

Stabilization:

Calibration:

Optimization:

SimBiology:

Derivation: Switch Model

Inducible Hbif Model

The Inducible Hbif Model describes how the switch flips when acted upon by the Lux/HSL-controlled expression of Hbif. In this model, [HSL] represents the concentration of the species HSL:pLux:LuxR, the complex that promotes the expression of Hbif. In this model [HSL] is a function of pLux and LuxR expression levels in the cell, the amount of HSL added, and the fractional occupancies at the complexation equilibrium. It can be assumed that this complexation reaction happens instantaneously with respect to the slow, rate-limiting translation step of Hbif. This model predicts the rate k1 of Lux-induced expression of Hbif, the degradation rate kdeg of Hbif, the forward and reverse rates k2 and k-2 of Hbif catalysis on the switch, and the equilibrium constant K2 for the switch when acted upon by Hbif.

Equation:

Reduction:

Solution:

Equilibration:

Stabilization:

Calibration:

Optimization of Hbif:

Optimization of ON:

SimBiology:

Derivation: Inducible Hbif Model

Team:Michigan/Modeling

From 2013.igem.org

Latest revision as of 23:58, 18 October 2013

Contents

Introduction

Switch modeling

Mass action modeling

Analytical modeling

Benefits

ERSESCO Algorithm

SimBiology

Expression Model

Switch Model

Inducible Hbif Model

@@ Line 1: / Line 1: @@
 {{:Team:Michigan_Template}}
-[[Team:Michigan/Modeling|Overview]]
-[[Team:Michigan/Modeling/Introduction|Introduction]]
-[[Team:Michigan/Modeling/Expression Model|Expression Model]]
-[[Team:Michigan/Modeling/Switch Model|Switch Model]]
-[[Team:Michigan/Modeling/Inducible Hbif Model|Inducible Hbif Model]]
-[[Team:Michigan/Modeling/Future Directions|Future Directions]]
-=[[Team:Michigan/Modeling|Overview]]=
+=Introduction=
-[[File:Best_model.jpg|900px|center]]
+===Switch modeling===
+The goal for our modeling was to create rigorous standard procedures for mathematically representing and analyzing systems.  Using our project as an example, we worked to demonstrate the viability of our approach by calculating the switch positions and optimum parameters.  This standardization should be useful in combination with system specific methods to create better modeling.
-===Model of Recombinase Expression===
+===Mass action modeling===
+Mass action is a form of modeling that uses systems of homogenous differential and difference equations.  Each equation is a sum of rates and each rate is proportional to the species involved.  The advantage is its straightforward uniform formulation, its minimal assumptions, and its flexibility of complexity.  Mass action itself uses very few assumptions but it can be used to represent systems of varying degrees of simplicity.  The fundamentals of chemical kinetics already champion the use of this modeling in its use of rate equations.  There chemical systems are completely defined by the products, reactants, and reaction rate constants.  This allows chemical modelling to be highly standardized and hence more accessible.  It's actually the uniform nature of mass action that's responsible.  Most importantly for iGEM, all mass action models can actually be put in a standard form as follows:
+[[File:mass action.png|670px|center]]
+• x is a species
-===Model of the Switch===
+• a is an amount of rates changing x
-===Model of Inducible Hbif===
+• b is a rate constant
-=[[Team:Michigan/Modeling/Introduction|Introduction]]=
+• c is a number of different species involved
-• switch modeling
+• d is a species involved
-    • goals: produce both states of switch, use model to optimize switch
+• e is a number of each species involved
-• mass action modeling
+• f is a number of species d involved
-    • what is mass action
+• g is a highest species involved
-• pros of mass action modeling, i.e. why we used it
+• l is a rate order
-• form of mass action models/solvability doc
+• m is the highest number of rates involved
-• analytical modeling
+• n is the number of species
-    • formulation
+===Analytical modeling===
+====Benefits====
+Given the parameters of the system, analytical (symbolic) modeling precisely predicts a system's behavior. Furthermore, unlike numerical methods, analytical modeling accurately predicts the data needed to determine parameters and avoids the inherent numerical rounding and approximation errors of more crude analyses.  Analytical modeling naturally lends itself to standardization because the results are unique to any given model.  Correct solutions, equilibria, eigenvalues, etc. will always have the same expression regardless of who or what calculated them.  The same can't be said for numerical methods.  With this and the iGEM community in mind, an analytical standard was developed that will allow for the exchange and automation of future modeling.
-    • reduction
+====ERSESCO Algorithm====
+The ERSESCO algorithm the Michigan team developed provides a clearly defined method for analyzing mathematical systems. The algorithm has seven major steps:
-    • solution
+'''1. Equation:'''
+Formulate the system into a system of differential equations.
-    • equilibration
+'''2. Reduction:'''
+Apply constraints, boundary conditions, and conservation laws to reduce the system of equations to fewer variables.
-    • stabilization
+'''3. Solution:'''
+Solve the reduced system of equations, if possible.
-    • calibration
+'''4. Equilibration:'''
+Find the steady states of the system by setting differential equations to zero and solving for critical points.
-    • optimization
+'''5. Stabilization:'''
+Evaluate the Jacobian matrix of the system of equations at each critical point and find the corresponding eigenvalues. To get stability, find the condition for which all eigenvalues have a negative real part.
+'''6. Calibration:'''
+Solve for the parameters of the system of equations in terms of the system's initial, steady state, time-dependent variables. This step allows the system parameters to be easily characterized using experimental data.
+'''7. Optimization:'''
+Optimize the steady state, eigenvalues, parameters, or other desired quantity by equating the derivative of that quantity with respect to each of the system's parameters with zero. Solving these equations gives the optimization conditions for that quantity.
+===SimBiology===
+SimBiology is a useful MATLAB package provided to all iGEM teams. It can be used as a tool to quickly run numerical approximations of biological systems whether or not data for system parameters are known. SimBiology can quickly produce a model from a simple schematic diagram. As a result, the package can quickly provide a qualitative analysis of a system with little work from the user.
+In the following models, our team applied our ERSESCO algorithm to fully analyze the systems at hand. Finally a SimBiology simulation was used as qualitative verification. We present the results from each step of the ERSESCO algorithm, followed by a SimBiology schematic with a graph showing the general behavior of the system, followed by a link to a more detailed derivation of the models.
+=Expression Model=
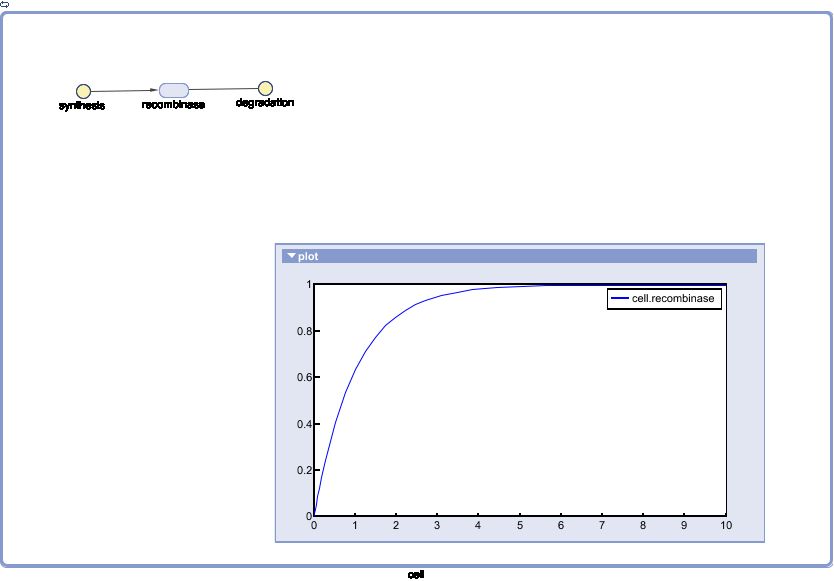
+The Recombinase Expression Model describes the synthesis and degradation of any protein produced at a relatively constant rate. Here, the model is used in particular to describe the synthesis and degradation reaction rates ksyn and kdeg of recombinases in the cell. The model also predicts the recombinase concentration.
-[[File:solvability.pdf|center]]
-=[[Team:Michigan/Modeling/Expression Model|Expression Model]]=
-[[File:Expression.jpg|center]]
 [[File:ExpressionModelFigure.png|center]]
+'''Equation:'''
 [[File:ExpressionModel1.png|218px|center]]
+'''Reduction: None'''
+'''Solution:'''
 [[File:ExpressionModel2.png|343px|center]]
+'''Equilibration:'''
 [[File:ExpressionModel3.png|128px|center]]
+'''Stabilization:'''
+[[File:ExpressionModel3-1.png|181px|center]]
+'''Calibration:'''
 [[File:ExpressionModel4.png|269px|center]]
 [[File:ExpressionModel5.png|322px|center]]
-=[[Team:Michigan/Modeling/Switch Model|Switch Model]]=
-[[File:Switch.jpg|center]]
+'''Optimization:'''
+[[File:ExpressionModel6.png|73px|center]]
+'''SimBiology:'''
+[[File:Expression.jpg|center]]
+'''Derivation:''' [https://docs.google.com/document/d/18ur0oiT7_mHhmd7Nk9vDJtsAGuFecNA1CtgTz9HAjsA/edit?usp=sharing Expression Model]
+=Switch Model=
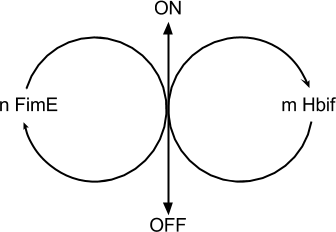
+The Switch Model describes how the switch equilibrates when the concentrations of the recombinases FimE and Hbif approach constant values.  The model assumes that each recombinase catalyzes a one way reaction. This model predicts the degree of cooperativity ''n'' and ''m'' in the binding reaction of the recombinase to DNA for FimE and Hbif, respectively. Furthermore, this model predicts the forward catalysis rate constants, ''kF'' and ''kH'', for FimE and Hbif.
 [[File:SwitchModelFigure.png|center]]
+'''Equation:'''
 [[File:SwitchModel1.png|395px|center]]
-[[File:SwitchModel2.png|158px|center]]
+[[File:SwitchModel2.png|280px|center]]
+'''Reduction:'''
 [[File:SwitchModel3.png|460px|center]]
+'''Solution:'''
+[[File:SwitchModel3-1.png|882px|center]]
+'''Equilibration:'''
 [[File:SwitchModel4-1.png|313px|center]]
-[[File:SwitchModel4-2.png|400px|center]]
+'''Stabilization:'''
+[[File:SwitchModel4-2.png|607px|center]]
+'''Calibration:'''
 [[File:SwitchModel5-1.png|640px|center]]
 [[File:SwitchModel5-2.png|752px|center]]
-<html>
-<iframe src="https://docs.google.com/document/d/1LewVc-RZQhwpdMyIHFYT9f4rbFrQXvppZOoQjKCZlLM/pub?embedded=true" width=100%></iframe>
-</html>
-=[[Team:Michigan/Modeling/Inducible Hbif Model|Inducible Hbif Model]]=
-[[File:InducedHbif.jpg|center]]
+'''Optimization:'''
+[[File:SwitchModel6.png|245px|center]]
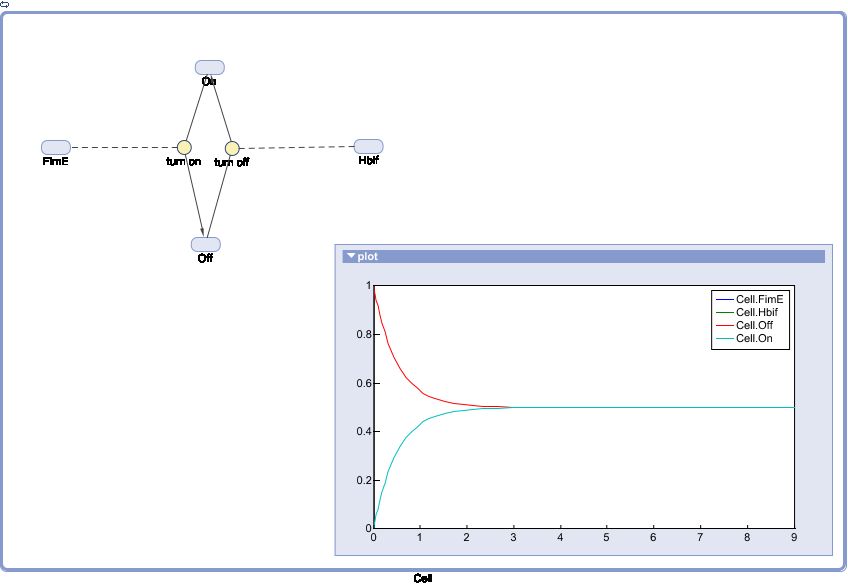
+'''SimBiology:'''
+[[File:Switch.jpg|center]]
+'''Derivation:''' [https://docs.google.com/document/d/1LewVc-RZQhwpdMyIHFYT9f4rbFrQXvppZOoQjKCZlLM/edit?usp=sharing Switch Model]
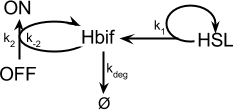
+=Inducible Hbif Model=
+The Inducible Hbif Model describes how the switch flips when acted upon by the Lux/HSL-controlled expression of Hbif. In this model, [HSL] represents the concentration of the species HSL:pLux:LuxR, the complex that promotes the expression of Hbif. In this model [HSL] is a function of pLux and LuxR expression levels in the cell, the amount of HSL added, and the fractional occupancies at the complexation equilibrium. It can be assumed that this complexation reaction happens instantaneously with respect to the slow, rate-limiting translation step of Hbif. This model predicts the rate k1 of Lux-induced expression of Hbif, the degradation rate kdeg of Hbif, the forward and reverse rates k2 and k-2 of Hbif catalysis on the switch, and the equilibrium constant K2 for the switch when acted upon by Hbif.
 [[File:InducibleHbifModelFigure.png|center]]
-System:
+'''Equation:'''
 [[File:InducibleHbifModel1.png |355px|center]]
-Conservation Equation:
 [[File:InducibleHbifModel2.png |242px|center]]
-Reduced System:
+'''Reduction:'''
 [[File:InducibleHbifModel3.png |460px|center]]
-Solution:
+'''Solution:'''
 [[File:InducibleHbifModel4.png |853px|center]]
-Steady State:
+'''Equilibration:'''
 [[File:InducibleHbifModel5.png |204px|center]]
-Calibration:
+'''Stabilization:'''
+[[File:InducibleHbifModel5-2.png |815px|center]]
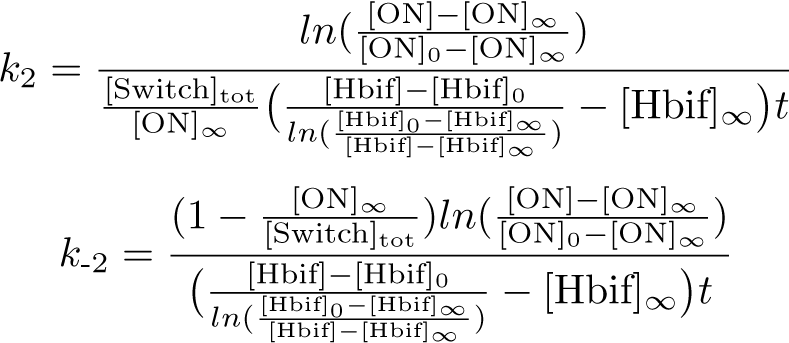
+'''Calibration:'''
 [[File:InducibleHbifModel6-1.png |335px|center]]
-[[File:InducibleHbifModel6-2.png |396px|center]]
+[[File:InducibleHbifModel6-2.png |395px|center]]
+[[File:InducibleHbifModel6-3.png |238px|center]]
-=[[Team:Michigan/Modeling/Future Directions|Future Directions]]=
-<!-- *** What falls between these lines is the Alert Box!  You can remove it from your pages once you have read and understood the alert *** -->
+'''Optimization of Hbif:'''
+[[File:InducibleHbifModel7-1.png |117px|center]]
-<html>
+'''Optimization of ON:'''
-<div id="box" style="width: 700px; margin-left: 137px; padding: 5px; border: 3px solid #000; background-color: #fe2b33;">
+[[File:InducibleHbifModel7-2.png |347px|center]]
-<div id="template" style="text-align: center; font-weight: bold; font-size: large; color: #f6f6f6; padding: 5px;">
-This is a template page. READ THESE INSTRUCTIONS.
-</div>
-<div id="instructions" style="text-align: center; font-weight: normal; font-size: small; color: #f6f6f6; padding: 5px;">
-You are provided with this team page template with which to start the iGEM season.  You may choose to personalize it to fit your team but keep the same "look." Or you may choose to take your team wiki to a different level and design your own wiki.  You can find some examples <a href="https://2008.igem.org/Help:Template/Examples">HERE</a>.
-</div>
-<div id="warning" style="text-align: center; font-weight: bold; font-size: small; color: #f6f6f6; padding: 5px;">
-You <strong>MUST</strong>  have all of the pages listed in the menu below with the names specified.  PLEASE keep all of your pages within your teams namespace.
-</div>
-</div>
-</html>
-<!-- *** End of the alert box *** -->
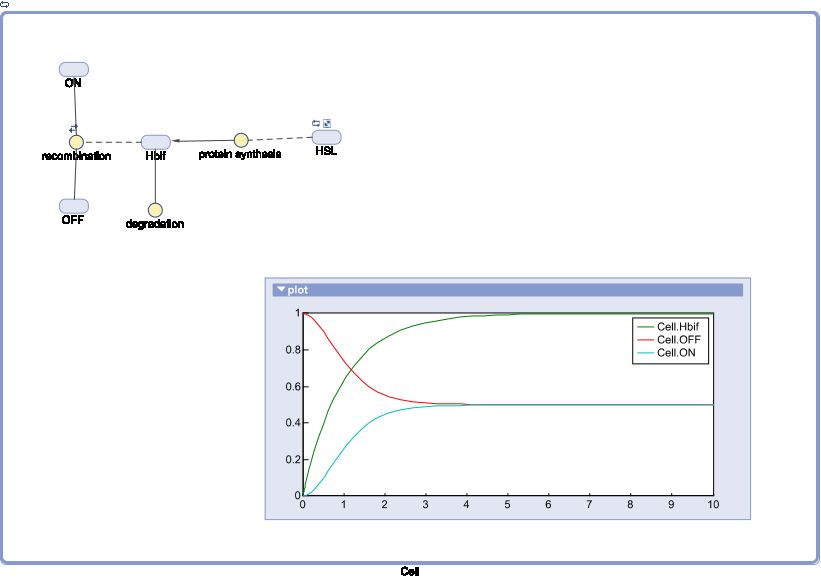
+'''SimBiology:'''
+[[File:InducedHbif.jpg|center]]
-{| style="color:#1b2c8a;background-color:#0c6;" cellpadding="3" cellspacing="1" border="1" bordercolor="#fff" width="62%" align="center"
+'''Derivation:''' [https://docs.google.com/document/d/1PNIkP84ksvYOu-HDYZghVVDkhDlMX7Iz9T6sFZnmfr8/edit?usp=sharing Inducible Hbif Model]
-!align="center"|[[Team:Michigan|Home]]
-!align="center"|[[Team:Michigan/Team|Team]]
-!align="center"|[https://igem.org/Team.cgi?year=2013&team_name=Michigan Official Team Profile]
-!align="center"|[[Team:Michigan/Project|Project]]
-!align="center"|[[Team:Michigan/Parts|Parts Submitted to the Registry]]
-!align="center"|[[Team:Michigan/Modeling|Modeling]]
-!align="center"|[[Team:Michigan/Notebook|Notebook]]
-!align="center"|[[Team:Michigan/Safety|Safety]]
-!align="center"|[[Team:Michigan/Attributions|Attributions]]
-|}