Team:NYMU-Taipei/Modeling/Linear epidemic model
From 2013.igem.org
| Line 1: | Line 1: | ||
{{:Team:NYMU-Taipei/Header}} | {{:Team:NYMU-Taipei/Header}} | ||
| - | == | + | ==Epidemic model== |
===Backgroud:=== | ===Backgroud:=== | ||
Revision as of 02:14, 28 September 2013


Contents |
Epidemic model
Backgroud:
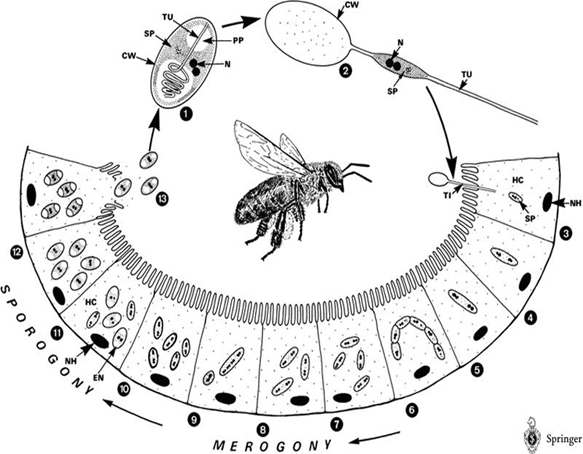
Honey bee is a social insect and can be divided into several classes – queens, drones, and workers, which can further be classified into field bee (which is responsible for getting honey from the nature) and house bee (which is responsible for cleaning hives). However, a single bee (especially field bee) may fall ill to CCD when it intakes water or food contaminated by Nosema ceranae spores. What’s worse, CCD may in turn spread to other bees through exchanging substances via mouthparts or feeding food to sacbroods.
After getting into bees’ midgut, Nosema spores will germinate, elongate its polarfilament, and pierce into midgut epithelial cells to transmit its genetic material. After finishing several life cycles, the infected epithelial cells will burst, leading to the spread of Nosema spores to nearby epithelial cells.
The life cycle of Nosema Ceranae:
The spores of Nosema ceranae:
The method is let bees ingest the encapsulated Bee. coli, which is suspended in sugar solution and will proliferate in bees’ midgut to build up bees’ immunity.
The purpose of this modeling:
- How many encapsulated Bee. Coli does a bee need to get immunized and be effective to spread our Bee. Coli to other bees and let the whole hive be immunized.
- How much time does the immunization requires and to see if it can save the whole society in time.
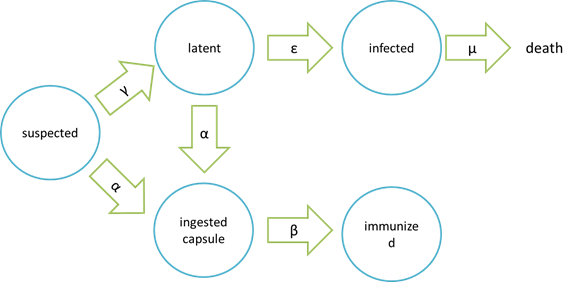
The assumption of infection and cure process:
Where “suspected” means the healthy bees, “latent” means the Nosema – infected but curable bees, “infected” means Nosema – infected bees which are incurable and doomed to death, “ingested capsule ” means bees with capsuled Bee. Coli, and “immunized” means bees immune to Nosema by Bee. coli intake.
It is assumed that the whole colony will only get into two consequences – one is dying out (once the “latent bees” turn to be the “infected bees”), and the other is survive (once the “latent” or “suspected bees” becomes “ingested capsule bees”).
Equation:
Parameters: N = total population S = suspected E = latent (eminent) I = infected C = ingested capsule R = immunized (recovery) α= suspected bees/ latent beesingested capsule bees rate constant γ= suspected bees latent bees rate constant β= ingested capsule bees immunized bees rate constant ε= latent bees infected bees rate constant μ= infected bees dead bees rate constant
Explanation: Since γSE represents the rate of suspected bees turning to latent bees by infected bees andαS the rate of suspected bees turning to ingested capsule bees after fed with sugar solution containing Bee. coli. The change rate of suspected bees(dS/dt) can therefore be expressed asγSE-αS.
Similarly, αE means the rate of latent bees turning to ingested capsule bees after fed with sugar solution containing Bee. coli andεE the rate of latent bees turning to infected bees without the treatment of Bee. coli. As a result, the change rate of latent bees(dE/dt) can therefore be expressed asγSE-εE-αE
Furthermore, μI is the rate of infected bees turning to dead bees, and thus, the change rate of infected bees (dI/dt) can therefore be expressed asεE-μI.
What’s more, βC represents the rate of ingested capsule bees turning to immunized bees after Bee. coli kicks in. The change rate of ingested capsule bees (dC/dt) and immunized bees(dR/dt)can therefore be expressed asαS +αE-βC andβC respectively.
The aim of the equation is to know the relationship of the number of all stages of bees (suspected, latent, infected, ingested capsule, immunized), namely, the survival and death rate under the influence of both Nosema infection and Bee. coli treatment over a specific period of time. For future prospect, the exponential epidemic model is considered more ideal and effective in spreading Bee. Coli throughout a bee colony. The only difference between linear and exponential epidemic model is that Bee. coli will proliferate exponentially in exponential epidemic model while in linear one , the number of Bee. coli is the same as the number of beads.
Result:
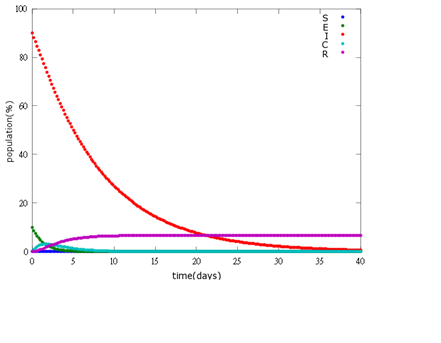
It is assumed that the whole bee colony is infected by Nosema, which is the most severe case. That is, bees are either latent or infected. According to our experiment, bees intaking sugar solution which contains capsules in a sufficient concentration have 100% of Bee. coli releasing from capsules. Here we discuss how much time it needs for the whole hive to recover from Nosema infection with different ratio of infected and latent stage.
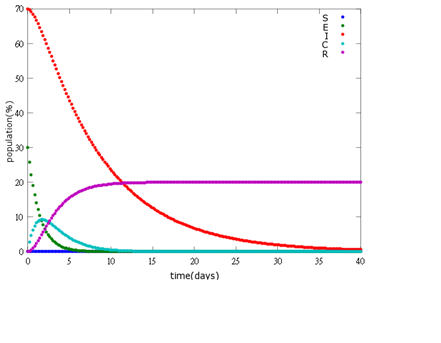
1. E=10%, I= 90%
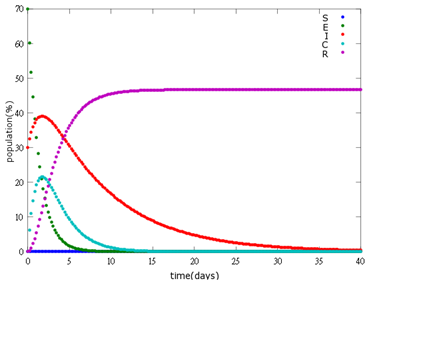
2. E=30%, I=70%:
3. E=70%, I=30%:
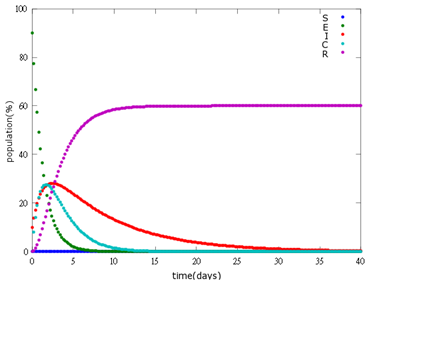
4. E=90%, 10%:
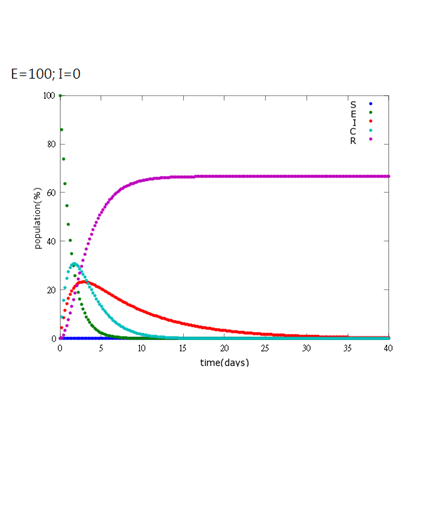
5. E=100%, I=0%:
As the pictures shows, the bigger the ratio of latent bees are, the more population of recovery bees are; the bigger the ratio of latent bees are, the lower the peak of infected bees’ population are; the bigger the ratio of latent bees are, the higher the peak of ingested capsule bees’ population are.
No matter which ratio of latent and infected bees is, it all shows that the whole bee colony will survive eventually, which fits our assumption that the whole colony will only get into two consequences – one is dying out (once the “latent bees” turn to be the “infected bees”), and the other is survive (once the “latent” or “suspected bees” becomes “ingested capsule bees”).
Background:
trxC promoter is an oxyR-activated promoter. Behind trxC promoter are several terminals to inhibit T7 polymerase-producing gene from being opened easily ; namely, it will not open until the concentration of oxyR is high enough, which means the bees are facing disastrous infection. Once oxyR concentration overcomes the threshold and conquers the terminal obstacles, T7 polymerase is produced and will bind to T7 promoter, which is a specific promoter binding only to T7 polymerase. Behind the T7promoter are enzyme PDC and ADH-producing genes, which will convert pyruvate to ethanol, and thus kill spores of Nosema Ceranae.
Pathway of ethanol:
PDC= pyruvate decarboxylase; ADH= Acetaldehyde
The purpose of this modeling is:
1.To simulate how many terminal do we need as a threshold to have the T7 polymerase-producing gene open at a proper time.
2.To simulate the threshold concentration of oxyR to conquer the terminal.
3.To determine the time of opening to see if the circuit could open in time (useful).
We assume that the equilibrium tendency of pyruvate to acetaldehyde is overwhelmingly rightward, while acetaldehyde to ethanol is bidirectional. We also assume that mRNA degrading rate is neglectable. As for how we measure promoter strengths, we choose PoPS, which is the rate of RNA polymerase binding to the DNA and trigger the transcription of the certain gene. It is assumed that the dose of pyruvate is sufficient in bees’ body through enough proliferation/copy number of Beecoli; the possibility of RNApolymerase skipping terminators is assumed to be proportional to time span; equilibrium between pyruvate and acetaldehyde is dominantly rightward, while equilibrium between acetaldehyde and ethanol is bidirectional; concentration of ethanol will not easily decrease and will sustain for a period of time.
Equation1:
1.KdROSoxyR = dissociation constant of ROSoxyR
2.n ROSoxyR = Hill coefficient of ROSoxyR
3.PoPStrxC = promoter strength of trxC
4.KdT7 = dissociation constant of T7
5.NT7 = Hill coefficient of T7
6.PoPST7 = promoter strength of T7 promoter
7.kdegmRNA = degrading constant of sensor promoter mRNA
8.N = number of plasmid in a single cell
9.V = volume of a cell
The aim of the equation is to know mRNA of T7 polymerase production rate and when it can reach the level to translate enough T7 poltmerase.
Equation2:
1.PoPStrxC = promotor strength of trxC promoter
2.PoPST7 = promoter strength of T7 promoter
3.RBS = binding site strength
4.kdegT7 = degrading constant of T7 polymerase
5.a = posibility of conquering the threshold concentration
6.n1 = Hill coefficient of ROSoxyR (complex of ROS+oxyR)
7.N = number of plasmid in a single cell
8.V = volume of a cell
The aim of the equation is to know the threshold concentration of oxyR to conquer the terminal and when T7 polymerase can reach the required concentration to activate T7 promoter.
Equation3:
1.KdT7 = dissociation constant of T7
2.NT7 = Hill coefficient of T7
3.PoPST7 = promoter strength of T7 promoter
4.kdegmRNA = degrading constant of sensor promoter mRNA
5.N = number of plasmid in a single cell
6.V = volume of a cell
The aim of the equation is to know mRNA of enzyme PDC production rate and when it can reach the level to translate enough PDC.
Equation4:
1.RBS = binding site strength
2.PoPST7 = promoter strength of T7 promoter
3.N = number of plasmid in a single cell
4.V = volume of a cell
5.KdegPDC = degrading constant of PDC (pyruvate decarboxylase)
The aim of the equation is to know PDC production rate and when it can reach the concentration of ethanol pathway equilibrium.
Equation5:
1.KdT7= dissociation constant of T7
2.NT7 = Hill coefficient of T7
3.PoPST7 = promoter strength of T7 promoter
4.kdegmRNA = degrading constant of sensor promoter mRNA
5.N = number of plasmid in a single cell
6.V = volume of a cell
 "
"