Team:Heidelberg/Templates/Modelling/Ind-Production
From 2013.igem.org
m |
|||
| Line 54: | Line 54: | ||
</ul> | </ul> | ||
| - | In addition, the experimental error for the observables was estimated with 2 error parameters and the initial concentration of the bacteria at t=0 was estimated. Data was otherwise normalized between 0 and 1, thus no scaling and offset parameters were required. | + | In addition, the experimental error for the observables was estimated with 2 error parameters and the initial concentration of the bacteria at t=0 was estimated. Data was otherwise normalized between 0 and 1, thus no scaling and offset parameters were required. In order to keep the model simple, it does not contain glutamine production, the initial glutamine concentration was arbitrarily set to 1. While this does not permit conclusions about absolute indigoidine synthesis rates, comparison of rates between the individual conditions is possible. |
<center> | <center> | ||
| Line 67: | Line 67: | ||
<h2 id="Results">Results</h2> | <h2 id="Results">Results</h2> | ||
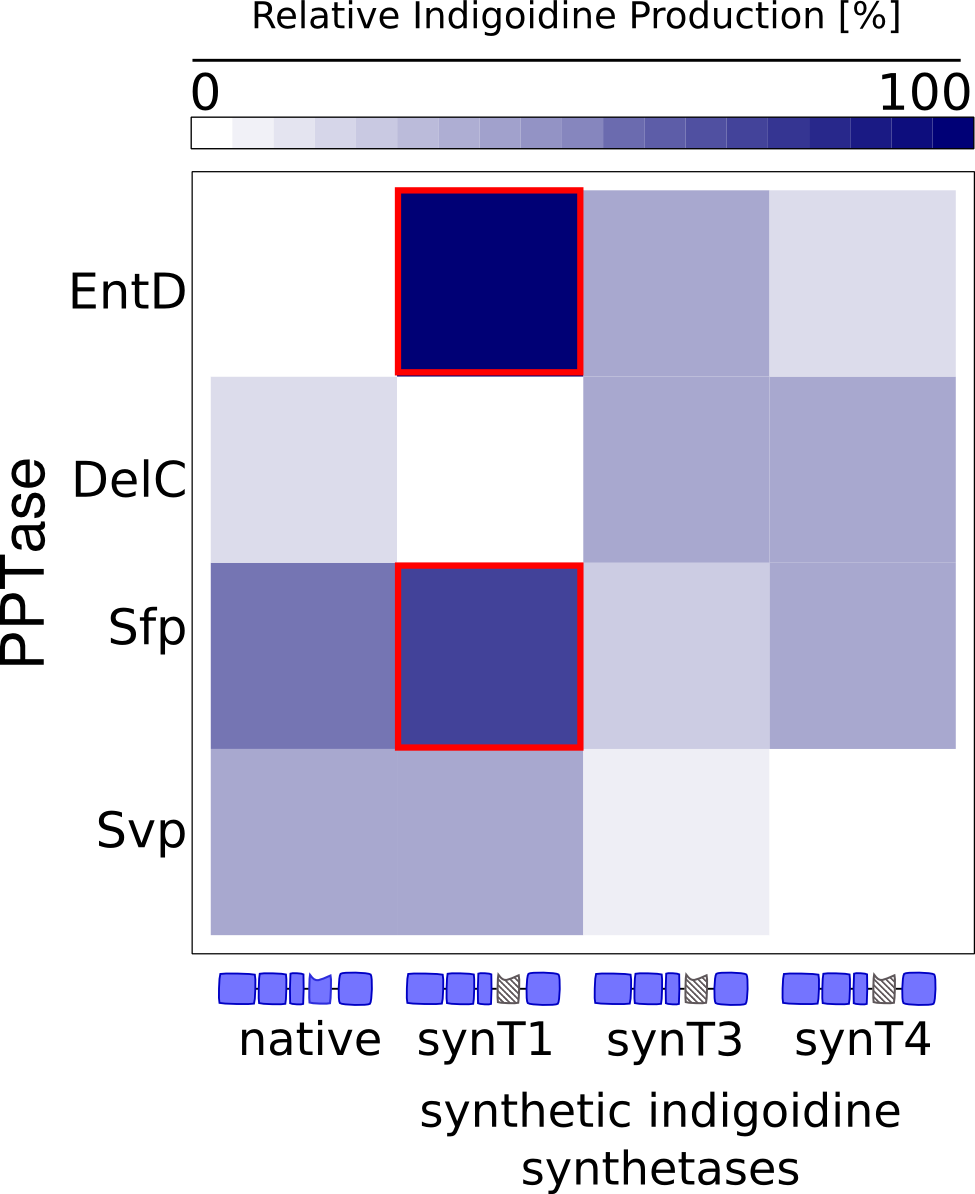
| + | The data sets could be grouped into two types, those with a significant indigoidine production and those without. Although both types of data sets resulted in seemingly good fits (Fig. 4), identifiability analysis using a profile likelihood exploiting approach<bib id="pmid19505944"/> showed that for all data sets without indigoidine production at least one parameter could not be reliably estimated (an exemplary plot is shown in Fig. 5B), whereas all parameters were identifiable for data sets showing indigoidine production (Fig. 5A). As our model only permits relative quantification of synthesis rates due to the lack of glutamine production and the arbitrarily chosen initial glutamine concentration, we normalized the indigoidine synthesis rates of the fully identifiable data sets to the range [0, 1] and visualized them in a heatmap (Fig. 3). The synthetic T domain T10 seems to be the most effective T domain for the entD and sfp PPTases, which corresponds very well to the preliminary analysis performed by the indigoidine team. | ||
| + | |||
<center> | <center> | ||
| - | <a class="fancybox fancyFigure" href="/wiki/images/ | + | <a class="fancybox fancyFigure" href="/wiki/images/4/45/Heidelberg_fit-native_sfp-T10_delC.png" title="<b>Figure 3: Experimental data and simulation of bacterial growth and indigoidine concentration.</b><b>A)</b>native_sfp. <b>B)</b> T10_delC."> |
| - | <img style="width: | + | <img style="width:100%; margin-bottom:10px; margin-top:10px; padding:1%;border-style:solid;border-width:1px;border-radius: 5px;" src="/wiki/images/4/45/Heidelberg_fit-native_sfp-T10_delC.png"/> |
| - | + | <figcaption style="width:100%"><b>Figure 3: Experimental data and simulation of bacterial growth and indigoidine concentration.</b><b>A)</b>native_sfp. <b>B)</b> T10_delC.</figcaption> | |
</a> | </a> | ||
</center> | </center> | ||
<center> | <center> | ||
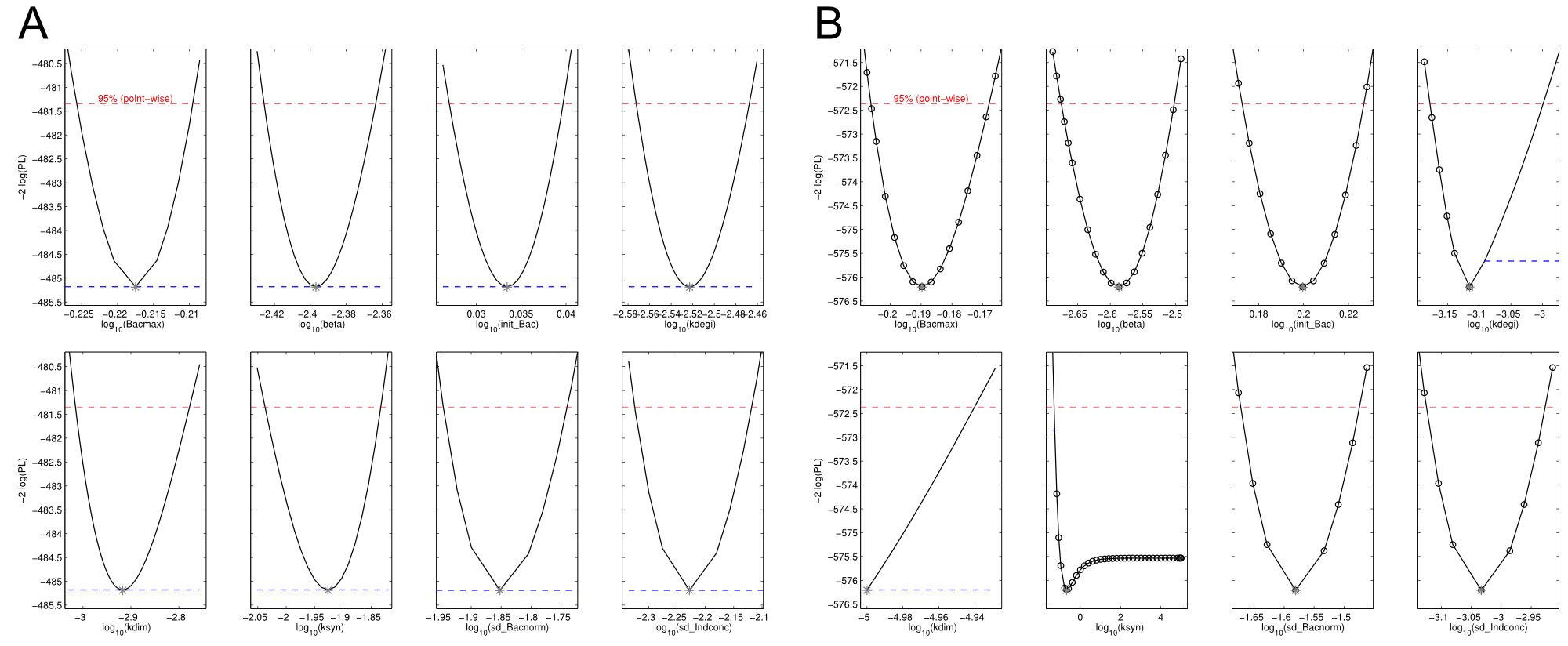
| - | <a class="fancybox fancyFigure" href="/wiki/images/ | + | <a class="fancybox fancyFigure" href="/wiki/images/9/94/Heidelberg_ple-native_sfp-T10_delC.png" title="<b>Figure 4: Identifiability analysis of the fitted parameters.</b><b>A)</b> native_sfp. <b>B)</b> T10_delC."> |
| - | <img style="width:100%; margin-bottom:10px; margin-top:10px; padding:1%;border-style:solid;border-width:1px;border-radius: 5px;" src="/wiki/images/ | + | <img style="width:100%; margin-bottom:10px; margin-top:10px; padding:1%;border-style:solid;border-width:1px;border-radius: 5px;" src="/wiki/images/9/94/Heidelberg_ple-native_sfp-T10_delC.png"/> |
| - | <figcaption style="width:100%"><b>Figure 4: | + | <figcaption style="width:100%"><b>Figure 4: Identifiability analysis of the fitted parameters.</b><b>A)</b> native_sfp. <b>B)</b> T10_delC.</figcaption> |
</a> | </a> | ||
</center> | </center> | ||
<center> | <center> | ||
| - | <a class="fancybox fancyFigure" href="/wiki/images/ | + | <a class="fancybox fancyFigure" href="/wiki/images/5/55/Heidelberg_heatmap_model1.png" title="<b>Figure 5: Indigoidine synthesis rates ksyn determined by fitting the model to several data sets</b>. The rates were normalized to the range between 0 and 1, rates for data sets where at least one parameter was not identifiable were set to 0. The synthetic T domain T10 is the most efficient of all tested T domains, whereas T12 is the only one that functions with all PPTases."> |
| - | <img style="width: | + | <img style="width:30%; margin-bottom:10px; margin-top:10px; padding:1%;border-style:solid;border-width:1px;border-radius: 5px;" src="/wiki/images/5/55/Heidelberg_heatmap_model1.png"/> |
| - | <figcaption style="width: | + | <figcaption style="width:60%;"><b>Figure 5: Indigoidine synthesis rates ksyn determined by fitting the model to several data sets</b>. The rates were normalized to the range between 0 and 1, rates for data sets where at least one parameter was not identifiable were set to 0. The synthetic T domain T10 is the most efficient of all tested T domains, whereas T12 is the only one that functions with all PPTases.</figcaption> |
</a> | </a> | ||
</center> | </center> | ||
Revision as of 02:40, 29 October 2013
Challenge
A challenge we had to face during the characterization and optimization of indC was to identify the production kinetics of Indigoidine. In order to disentangle the underlying mechanisms of bacterial growth and peptide synthesis, we decided to set up a mathematical model based on coupled ordinary differential equations (ODEs). Calibrated with our experimental time-resolved data, the mathematical model could potentially not only elucidate how Indigoidine production influences growth of bacteria but also provide a more quantitative understanding of the synthesis efficiency of the different T domains and PPTases that were tested.Approach
First, we set up a mind model based on the fact that the functional Indigoidine dimer is produced from two Glutamine (Glu) that are each cyclized (cGlu) ref[Brachmann, Alexander O, Kirchner, Ferdinand, Kegler, Carsten, Kinski, Sebastian C, Schmitt, Imke, Bode, Helge B: Triggering the production of the cryptic blue pigment indigoidine from Photorhabdus luminescens., J. Biotechnol. 157(1), 96–9, January 2012] (Fig. 1), and our observation that Indigoidine (Ind)-producing bacteria (Bac) grow slower than mock controls. Those hypotheses resulted in a general model scheme depicting the interdependency between Indigoidine synthesis and bacterial growth. With the mathematical model we could then validate whether there is indeed a negative feedback from the Indigoidine production to the growth of bacteria.

Since we had already established our quantitative Indigoidine production assay (see Tag-Optimization) in a time-dependent manner, we wanted to further exploit these experimental data via quantitative dynamic modeling. The change of bacteria and Indigoidine with time was measured via optical density of the liquid cultures in a 96-well plate of a TECAN reader and can be described in ordinary differential equations (ODEs). Such ODEs contain parameters that characterize e.g. growth or synthesis rates for bacteria or Indigoidine, respectively.
Ordinary Differential Equations (ODEs)
But how to find proper equations for bacterial growth and indigoidine synthesis? From our mind model (Fig. 2), we derived ODEs based on mass-action kinetics\begin{align} \mathrm{d}\mathrm{[Bac]}/\mathrm{d}t &= \frac{\mathrm{[Bac]} \cdot \left(\mathrm{[Bac]} - \mathrm{Bacmax}\right) \cdot \mathrm{beta}}{\mathrm{Bacmax}}\label{bacgrowth}\\ \mathrm{d}\mathrm{[Glu]}/\mathrm{d}t &= - \mathrm{[Bac]} \cdot \mathrm{[Glu]} \cdot \mathrm{ksyn}\label{glu}\\ \mathrm{d}\mathrm{[cGlu]}/\mathrm{d}t &= - \mathrm{kdim} \cdot {\mathrm{[cGlu]}}^2 + \mathrm{[Bac]} \cdot \mathrm{[Glu]} \cdot \mathrm{ksyn}\label{cglu}\\ \mathrm{d}\mathrm{[Ind]}/\mathrm{d}t &= {\mathrm{[cGlu]}}^2 \cdot \mathrm{kdim} - \mathrm{[Ind]} \cdot \mathrm{kdegi}\label{ind} \end{align}
Initially, inhibition of bacterial growth by indigoidine and degradation of cyclic glutamine were also described by the model, using equations \eqref{bacgrowthinhib} and \eqref{cgludeg} instead of \eqref{bacgrowth} and \eqref{cglu}, respectively, however the degradation rate turned out to be non-identifiable for all data sets, converging to the lower bound, whereas the growth inhibition term led to frequent convergence failures, the inhibition constant being very low in cases where convergence was achieved. These two terms were thus removed from the model. \begin{align} \mathrm{d}\mathrm{[Bac]}/\mathrm{d}t &= \frac{\mathrm{[Bac]} \cdot \left(\mathrm{[Bac]} - \mathrm{Bacmax}\right) \cdot \left(\mathrm{beta} - \mathrm{ki} \cdot \mathrm{[Ind]}\right)}{\mathrm{Bacmax}}\label{bacgrowthinhib}\\ \mathrm{d}\mathrm{[cGlu]}/\mathrm{d}t &= - \mathrm{kdim} \cdot {\mathrm{[cGlu]}}^2 - \mathrm{kdegg} \cdot \mathrm{[cGlu]} + \mathrm{[Bac]} \cdot \mathrm{[Glu]} \cdot \mathrm{ksyn}\label{cgludeg} \end{align}
This system contains 4 dynamic variables: Bacteria (Bac), Glutamine (Glu), cyclized Glutamine (cGlu) and Indigoidine (Ind) that change with time t. Bacteria and Indigoidine was experimentally measured, we thus call Bac and Ind observables of our system. The equations are described by 5 kinetic parameters:- Bacmax: maximum capacity for bacterial growth
- beta: maximum attainable growth rate
- ksyn: synthesis rate of cyclized glutamine from glutamine
- kdim: dimerization rate of two cyclized glutamines to an Indigoidine dimer
- kdegi: degradation rate of indigoidine

Framework
Parameters have to be estimated from experimental data. In order to implement our mathematical model and the wetlab data, we used an open-source software package allowing for comprehensive analysis (D2D Software). With this framework, we were able to calibrate the model and perform robust parameter estimationsResults
The data sets could be grouped into two types, those with a significant indigoidine production and those without. Although both types of data sets resulted in seemingly good fits (Fig. 4), identifiability analysis using a profile likelihood exploiting approach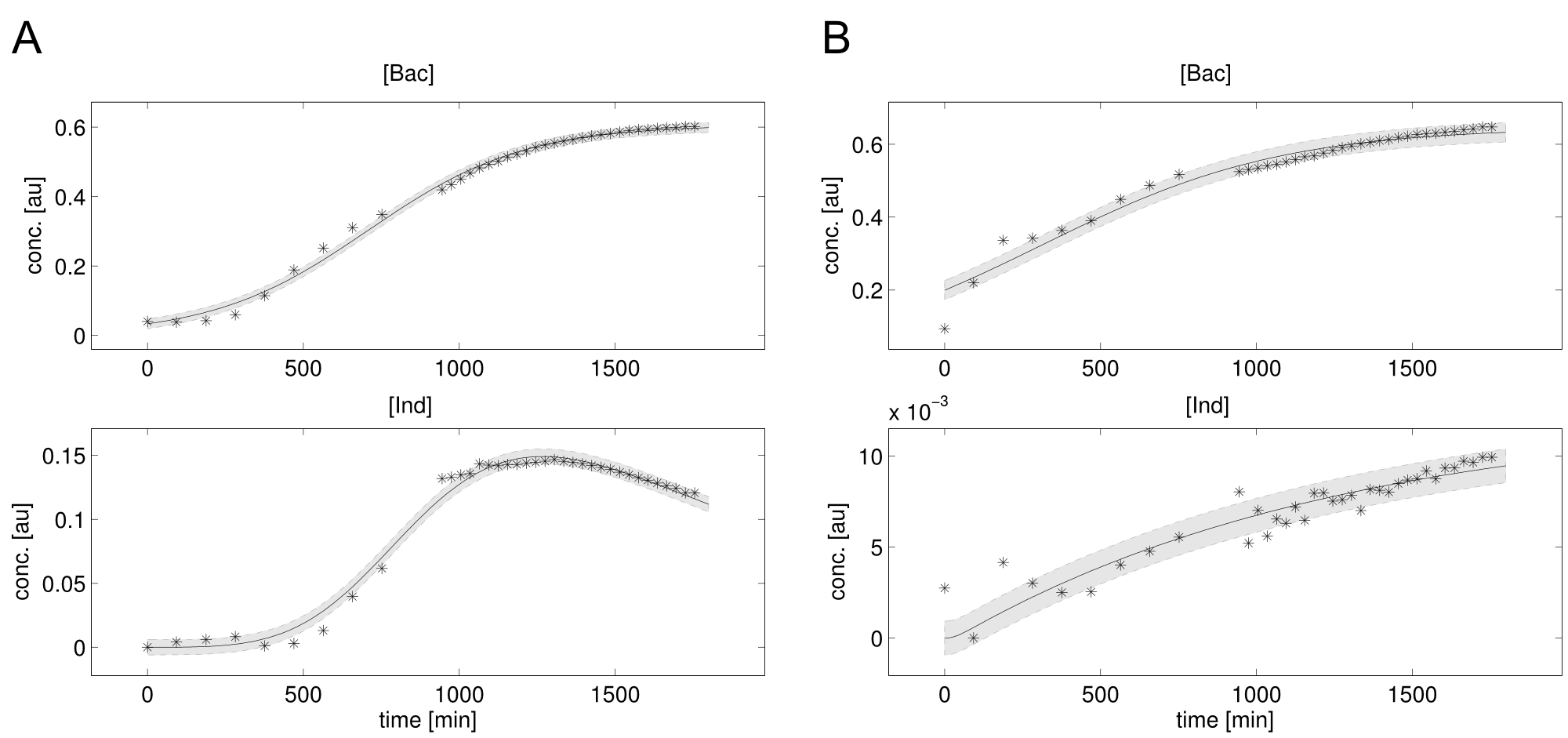
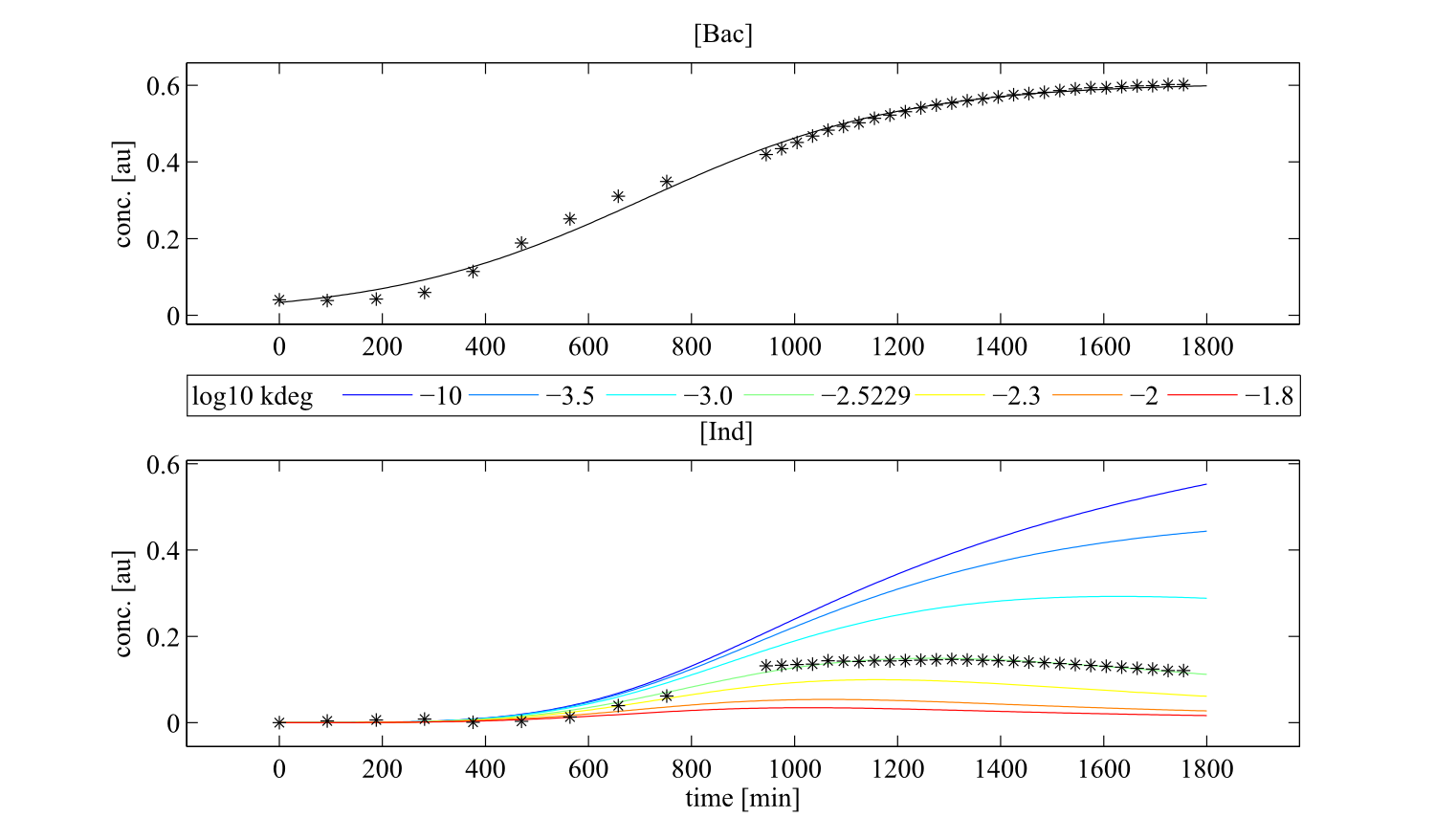
Sensitivity analysis for optimized indigoidine production
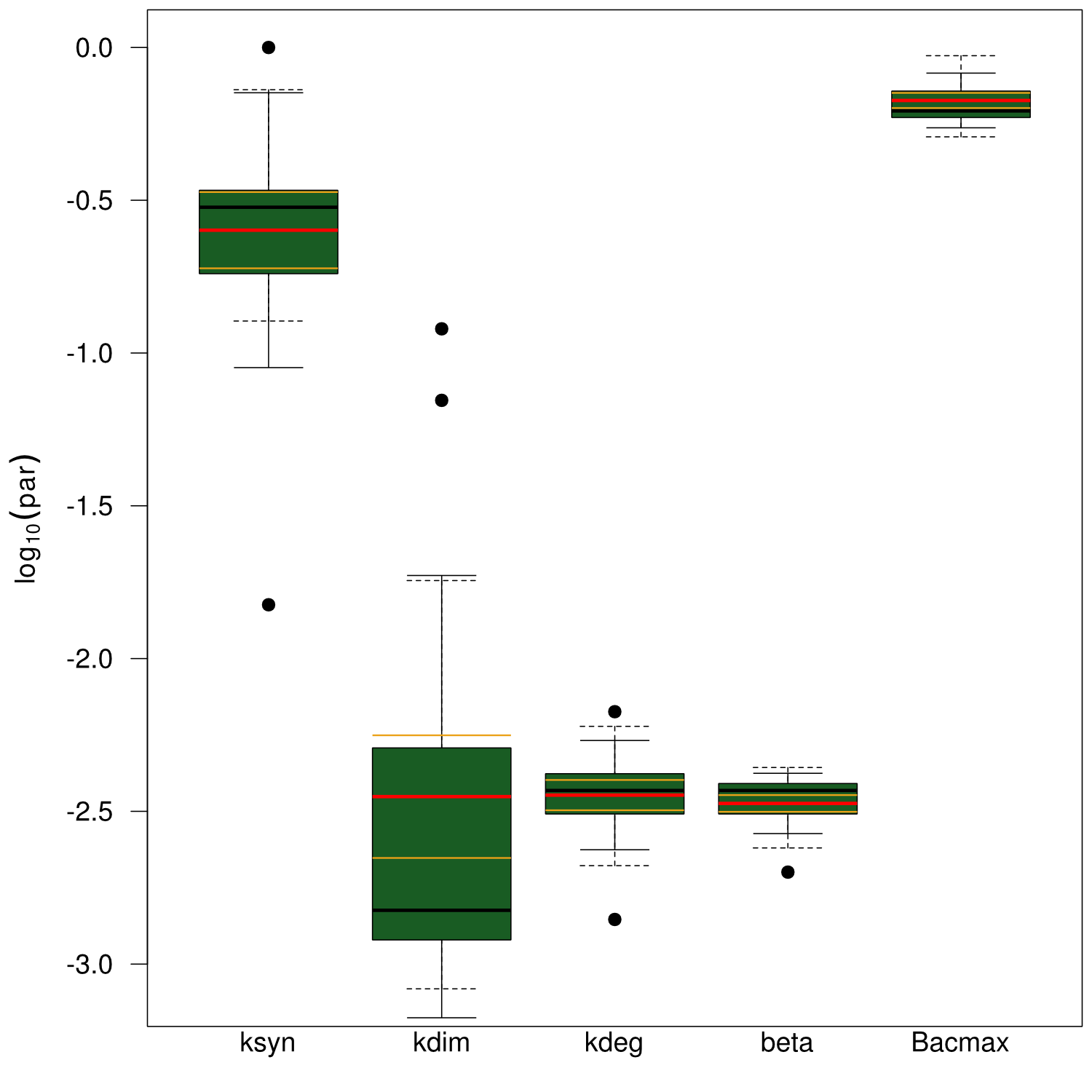
To perceive the role of kdegi for indigoidine synthesis, we have varied the parameter over a broad range and observed qualitatively distinct model trajectories. For a more quantitative understanding of how indigoidine yield changes with altering parameters of the system, we conducted a sensitivity analysis (REVIEW NEEDED). Therefore, we first defined the variable IntInd, the integrated indigoidine reflecting production yield. The change of the indigoidine concentration with time is determined by the ODE (4) and its integral with time can be depicted as the area under the [Ind] curve, i.e. the amount of indigoidine produced by the bacteria with time. Now we were interested in the change of IntInd with the change of the different parameters of our system. Mathematically, this is expressed as the so called sensitivity $\frac{\partial \mathrm{X}}{\partial \mathrm{p}}, with X as our variable of interest (IntInd) and p as the parameter (beta, Bacmax, ksyn, kdim or kdegi, respectively). This partial derivative provides a measure of how much X changes with the change of p or how sensitive X is against small variations in p. Sensitivities can be scaled with the actual values of X and the respective p to fall in the range from -1 to +1. The higher the absolute value of the sensitivity, the more important is the parameter for the variable. A positive sensitivity means positive impact of the parameter on the variable whereas a sensitivity < 0 indicates reduction of X for subtle decrease in p. We utilised our mathematical model and computed the sensitivities of IntInd against the change of all five kinetic parameters of our system and scaled them accordingly. The analysis confirmed that the kdegi was the only parameter of the system that exhibited a negative impact on the indigoidine production (Tab. 1). Slight increase of all the other parameters also augmented additional yield. Sensitivity analysis for native_sfp:| Parameter | $$\left.\mathrm{[Bac]}\right|_{t=0}$$ | kdegi | kdim | beta | ksyn | Bacmax |
|---|---|---|---|---|---|---|
| $$\frac{\partial\int\!\mathrm{Ind}\,\mathrm{d}t}{\partial p}$$ | 0.784 | -0.7024 | 0.5117 | 0.3338 | 0.2919 | 0.1036 |
 "
"