Team:Heidelberg/Templates/Modelling/Ind-Production
From 2013.igem.org
m |
m |
||
| Line 5: | Line 5: | ||
In order to disentangle the underlying mechanisms of bacterial growth and peptide synthesis, we decided to set up a mathematical model based on coupled ordinary differential equations (ODEs). Calibrated with <a class="fancybox fancyGraphical" href="https://static.igem.org/mediawiki/2013/3/38/Heidelberg_IndPD_Fig11.png" caption="<b>Figure 9: Indigoidine Production Varies Among Engineered Indigoidine Synthetases.</b> | In order to disentangle the underlying mechanisms of bacterial growth and peptide synthesis, we decided to set up a mathematical model based on coupled ordinary differential equations (ODEs). Calibrated with <a class="fancybox fancyGraphical" href="https://static.igem.org/mediawiki/2013/3/38/Heidelberg_IndPD_Fig11.png" caption="<b>Figure 9: Indigoidine Production Varies Among Engineered Indigoidine Synthetases.</b> | ||
The absorption spectrum of liquid cultures expressing engineered variants of the indC indigoidine synthetase were measured for 30 hours. The graphs show the OD590 of indigoidine in <i>E. coli</i> liquid cultures over time. The absorption of the cell suspension has been subtracted (see OD Measurement in the Methods section). The red graph relates to an <i>E. coli</i> TOP10 negative control, the green graph depicts the indigoidine production of an indC variant, in which the T-domain has been exchanged with our synthetic T-domain #3, whereas the blue graphs refers to synthetic T-domain #4. | The absorption spectrum of liquid cultures expressing engineered variants of the indC indigoidine synthetase were measured for 30 hours. The graphs show the OD590 of indigoidine in <i>E. coli</i> liquid cultures over time. The absorption of the cell suspension has been subtracted (see OD Measurement in the Methods section). The red graph relates to an <i>E. coli</i> TOP10 negative control, the green graph depicts the indigoidine production of an indC variant, in which the T-domain has been exchanged with our synthetic T-domain #3, whereas the blue graphs refers to synthetic T-domain #4. | ||
| - | The amount of indigoidine reaches a maximum before it drops again. This is due the instability of indigoidine, which is reduced to its fluorescent leuco-form under the influence of reducing agents, light and high temperature | + | The amount of indigoidine reaches a maximum before it drops again. This is due the instability of indigoidine, which is reduced to its fluorescent leuco-form under the influence of reducing agents, light and high temperature<bib id="pmid17237222"/>. The local absorption maximum at 590 nm (keto-indigoidine) decreases after 15-25 hours, whereas the absorption maximum at 430 nm (leuco-indigoidine) increases (data not shown). Note that the maximum level of indigoidine differs among the engineered indigoidine synthetases.">our experimental time-resolved data</a>, the mathematical model could potentially not only elucidate how indigoidine production influences growth of bacteria but also provide a more quantitative understanding of the synthesis efficiency of <a class="fancybox fancyGraphical" href="https://static.igem.org/mediawiki/2013/4/4d/Heidelberg_IndPD_Fig10.png" caption="<b>Figure 8: Indigoidine Production Depend on Combination of T-domain and PPTase</b> |
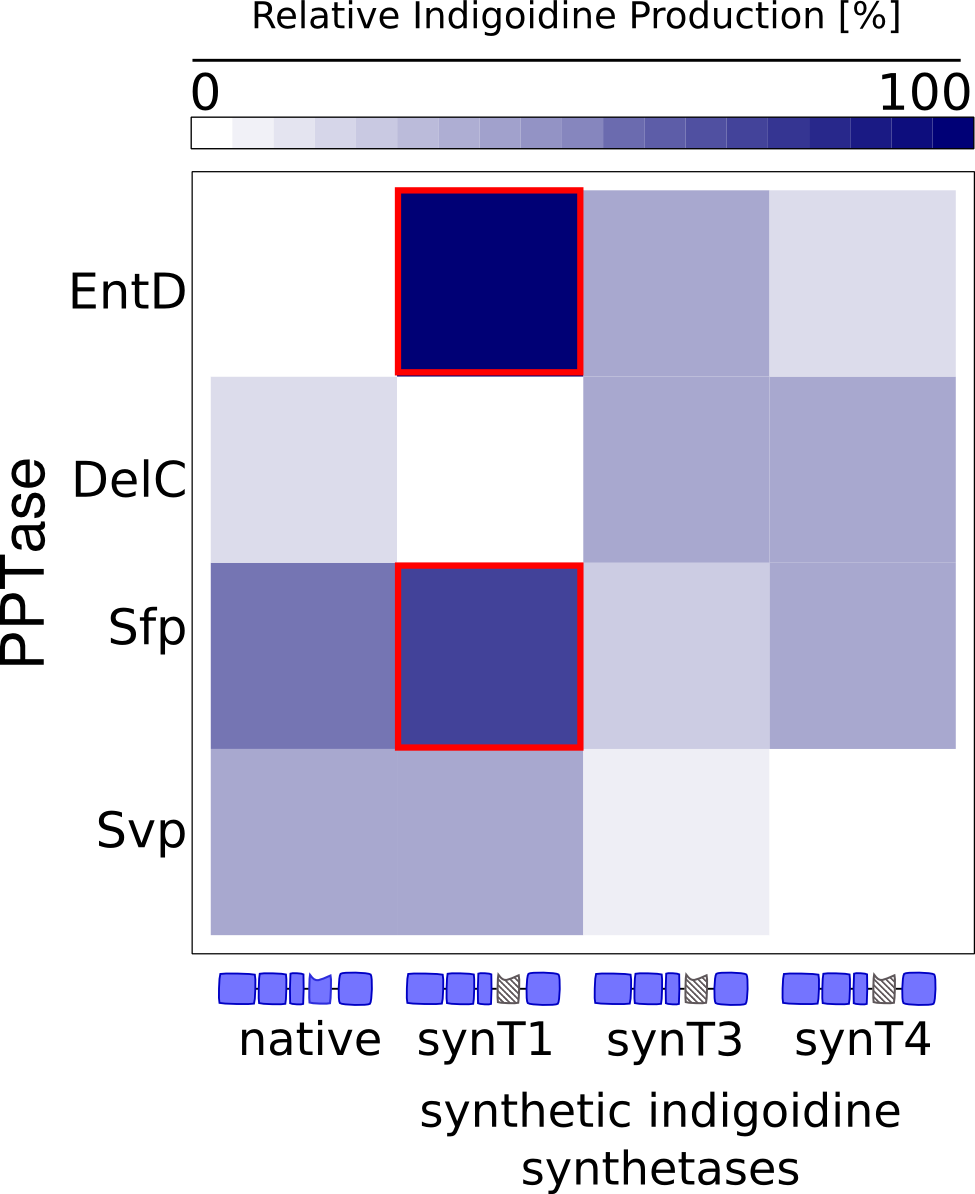
The absorption spectrum of liquid cultures expressing engineered variants of the indC indigoidine synthetase were measured for 30 hours. The graphs show the OD590 of indigoidine in <i>E. coli</i> liquid cultures over time. The absorption of the cell suspension has been subtracted (see OD Measurement in the Methods section). The left diagram shows the indigoidine production over time of a liquid culture expressing an engineered indigoidine synthetase with the synthetic T-domain #1 (synT1) and a PPTase, whereas each graph refers to a specific PPTase coexpressed. The diagram on the right shows the corresponding data for the indigoidine synthetase with the synthetic T-domain #3 (synT3). | The absorption spectrum of liquid cultures expressing engineered variants of the indC indigoidine synthetase were measured for 30 hours. The graphs show the OD590 of indigoidine in <i>E. coli</i> liquid cultures over time. The absorption of the cell suspension has been subtracted (see OD Measurement in the Methods section). The left diagram shows the indigoidine production over time of a liquid culture expressing an engineered indigoidine synthetase with the synthetic T-domain #1 (synT1) and a PPTase, whereas each graph refers to a specific PPTase coexpressed. The diagram on the right shows the corresponding data for the indigoidine synthetase with the synthetic T-domain #3 (synT3). | ||
The indigoidine production correlates to the combination of a T-domain with a respective PPTase and the PPTases vary in their ability to activate T-domains. For example, DelC is unable to activate synT 1 but activates synT3, whereas svp activates synT1 but is unable to activate synT3. Note also, that activation of synT3 by EntD results in the highest amount of indigoidine production among all the combinations shown.">the different T domains and PPTases</a> that were tested. | The indigoidine production correlates to the combination of a T-domain with a respective PPTase and the PPTases vary in their ability to activate T-domains. For example, DelC is unable to activate synT 1 but activates synT3, whereas svp activates synT1 but is unable to activate synT3. Note also, that activation of synT3 by EntD results in the highest amount of indigoidine production among all the combinations shown.">the different T domains and PPTases</a> that were tested. | ||
| Line 11: | Line 11: | ||
<h2 id="Approach"> Approach </h2> | <h2 id="Approach"> Approach </h2> | ||
<p> | <p> | ||
| - | First, we set up a mind model based on the fact that the functional indigoidine dimer is produced from two glutamines (Glu) that are each cyclized (cGlu) | + | First, we set up a mind model based on the fact that the functional indigoidine dimer is produced from two glutamines (Glu) that are each cyclized (cGlu)<bib id="pmid22085970"/> (<a class="fancybox fancyFigure" href="/wiki/images/8/83/Heidelberg_IndSynthesis_scheme.png" title="<b>Figure 1: The indigoidine synthetase indC produces a blue pigment and is used for the indigoidine-tag</b>. After activation of L-glutamine by the A domain and its binding to the T domain, it is cyclized by the TE domain and oxidized by the Ox domain. Dimerization is thought to happen by air.">Fig. 1</a>), and our observation that indigoidine (Ind)-producing bacteria (Bac) <a class="fancybox fancyGraphical" href="https://static.igem.org/mediawiki/2013/c/cf/Heidelberg_IndPD_Fig6.png" caption="<b>Figure 3: Comparison between different <em>E. coli</em> strains and PPTases:</b> |
<b>a)</b> Comparison of different <em>E. coli</em> strains examining growth and indigoidine production | <b>a)</b> Comparison of different <em>E. coli</em> strains examining growth and indigoidine production | ||
The figure shows five different strains of <em>E. coli</em> that have been co-transformed with an indC expression plasmid and a sfp expression plasmid. The negative control is <em>E. coli</em> TOP10 without a plasmid. All transformants have been grown on LB agar for 48 hours at room temperature, cells were not induced. One can see that even without induction all strains express the indigoidine synthetase and produce the blue pigment indigoidine. However, the strains BAP1 and NEB Turbo grow faster in the first day, exhibiting a white phenotype (data not shown). Colonies on the plate of <em>E. coli</em> TOP10 are very small and dark blue/ black. Assuming that indigoidine production inhibits cell growth due to its toxicity, we concluded that TOP10 produced the most indigoidine among the strains we tested. We used <em>E. coli</em> TOP10 for the following experiments. | The figure shows five different strains of <em>E. coli</em> that have been co-transformed with an indC expression plasmid and a sfp expression plasmid. The negative control is <em>E. coli</em> TOP10 without a plasmid. All transformants have been grown on LB agar for 48 hours at room temperature, cells were not induced. One can see that even without induction all strains express the indigoidine synthetase and produce the blue pigment indigoidine. However, the strains BAP1 and NEB Turbo grow faster in the first day, exhibiting a white phenotype (data not shown). Colonies on the plate of <em>E. coli</em> TOP10 are very small and dark blue/ black. Assuming that indigoidine production inhibits cell growth due to its toxicity, we concluded that TOP10 produced the most indigoidine among the strains we tested. We used <em>E. coli</em> TOP10 for the following experiments. | ||
| Line 107: | Line 107: | ||
Our mathematical model was able to describe most of our experimental data and was in those cases structurally and practically fully identifiable. We thus challenged the model to deduce additional facts on indigoidine synthesis. | Our mathematical model was able to describe most of our experimental data and was in those cases structurally and practically fully identifiable. We thus challenged the model to deduce additional facts on indigoidine synthesis. | ||
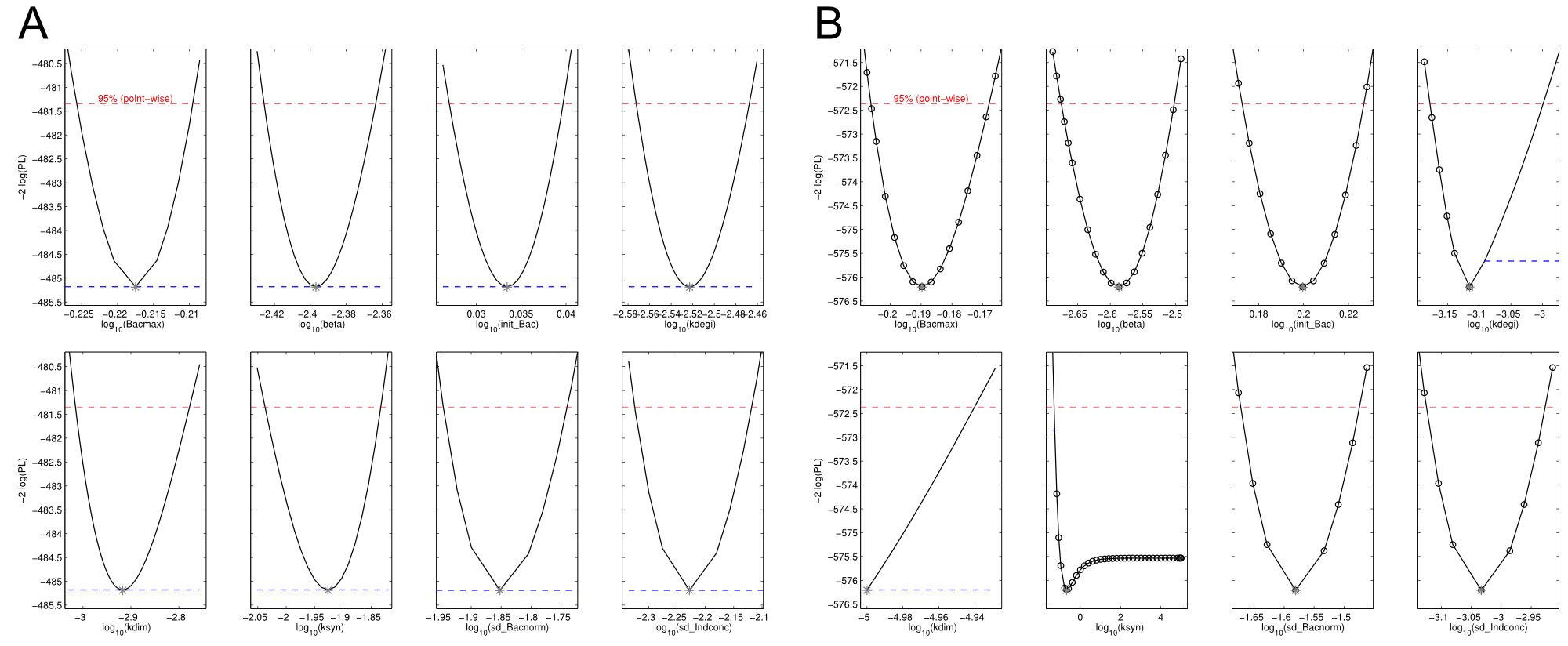
| - | First, we had a look at the parameters that were estimated to describe our experimental data sets. For each parameter estimate, the lower boundary was set to 1e-5 and the upper boundary was set to 1e+5. Initial guesses for parameters during parameter estimations were generated via latin hypercube sampling to ensure broad coverage of all regions in the high-dimensional parameter space<bib id="jstor2346140"/>. Nevertheless, some parameters exhibited broad variation among the best fits of the different data sets while other parameters were estimated in a narrow range (Fig. | + | First, we had a look at the parameters that were estimated to describe our experimental data sets. For each parameter estimate, the lower boundary was set to 1e-5 and the upper boundary was set to 1e+5. Initial guesses for parameters during parameter estimations were generated via latin hypercube sampling to ensure broad coverage of all regions in the high-dimensional parameter space<bib id="jstor2346140"/>. Nevertheless, some parameters exhibited broad variation among the best fits of the different data sets while other parameters were estimated in a narrow range (<a class="fancybox fancyFigure" href="/wiki/images/d/d9/Heidelberg_boxplot1.png" title="<b>Figure 7: Box and whiskers plot of the parameters fitted for the invidual data sets.</b> The black line represents the median, the box ranges from the first to the third quartile of the sample. The dashed whiskers denote the median ± 1.5 times the interquartile range. The red line denotes the mean, yellow lines the mean ± standard error of the mean, solid whiskers the mean ± standard deviation.">Fig. 7</a>). |
</p> | </p> | ||
<center> | <center> | ||
Revision as of 03:46, 29 October 2013
Challenge
A challenge we had to face during the characterization and optimization of indC was to identify the production kinetics of indigoidine. In order to disentangle the underlying mechanisms of bacterial growth and peptide synthesis, we decided to set up a mathematical model based on coupled ordinary differential equations (ODEs). Calibrated with . The local absorption maximum at 590 nm (keto-indigoidine) decreases after 15-25 hours, whereas the absorption maximum at 430 nm (leuco-indigoidine) increases (data not shown). Note that the maximum level of indigoidine differs among the engineered indigoidine synthetases.">our experimental time-resolved data, the mathematical model could potentially not only elucidate how indigoidine production influences growth of bacteria but also provide a more quantitative understanding of the synthesis efficiency of the different T domains and PPTases that were tested.Approach
First, we set up a mind model based on the fact that the functional indigoidine dimer is produced from two glutamines (Glu) that are each cyclized (cGlu)

Since we had already established our quantitative indigoidine production assay (see Tag-Optimization) in a time-dependent manner, we wanted to further exploit these experimental data via quantitative dynamic modeling. The change of bacteria and Indigoidine with time was measured via optical density of the liquid cultures in a 96-well plate of a TECAN reader and can be described in ordinary differential equations (ODEs). Such ODEs contain parameters that characterize e.g. growth or synthesis rates for bacteria or indigoidine, respectively.
Ordinary Differential Equations (ODEs)
How to find proper equations for bacterial growth and indigoidine synthesis?
From our mind model (Fig. 2), we derived ODEs based on mass-action kinetics
\begin{align} \mathrm{d}\mathrm{[Bac]}/\mathrm{d}t &= \frac{\mathrm{[Bac]} \cdot \left(\mathrm{[Bac]} - \mathrm{Bacmax}\right) \cdot \mathrm{beta}}{\mathrm{Bacmax}}\label{bacgrowth}\\ \mathrm{d}\mathrm{[Glu]}/\mathrm{d}t &= - \mathrm{[Bac]} \cdot \mathrm{[Glu]} \cdot \mathrm{ksyn}\label{glu}\\ \mathrm{d}\mathrm{[cGlu]}/\mathrm{d}t &= - \mathrm{kdim} \cdot {\mathrm{[cGlu]}}^2 + \mathrm{[Bac]} \cdot \mathrm{[Glu]} \cdot \mathrm{ksyn}\label{cglu}\\ \mathrm{d}\mathrm{[Ind]}/\mathrm{d}t &= {\mathrm{[cGlu]}}^2 \cdot \mathrm{kdim} - \mathrm{[Ind]} \cdot \mathrm{kdegi}\label{ind} \end{align}
Initially, inhibition of bacterial growth by indigoidine and degradation of cyclic glutamine were also described by the model, using equations \eqref{bacgrowthinhib} and \eqref{cgludeg} instead of \eqref{bacgrowth} and \eqref{cglu}, respectively, however the degradation rate turned out to be non-identifiable for all data sets, converging to the lower bound, whereas the growth inhibition term led to frequent convergence failures, the inhibition constant being very low in cases where convergence was achieved. These two terms were thus removed from the model. \begin{align} \mathrm{d}\mathrm{[Bac]}/\mathrm{d}t &= \frac{\mathrm{[Bac]} \cdot \left(\mathrm{[Bac]} - \mathrm{Bacmax}\right) \cdot \left(\mathrm{beta} - \mathrm{ki} \cdot \mathrm{[Ind]}\right)}{\mathrm{Bacmax}}\label{bacgrowthinhib}\\ \mathrm{d}\mathrm{[cGlu]}/\mathrm{d}t &= - \mathrm{kdim} \cdot {\mathrm{[cGlu]}}^2 - \mathrm{kdegg} \cdot \mathrm{[cGlu]} + \mathrm{[Bac]} \cdot \mathrm{[Glu]} \cdot \mathrm{ksyn}\label{cgludeg} \end{align}
This system contains 4 dynamic variables: Bacteria (Bac), Glutamine (Glu), cyclized Glutamine (cGlu) and Indigoidine (Ind) that change with time t. Bacteria and Indigoidine was experimentally measured, we thus call Bac and Ind observables of our system. The equations are described by 5 kinetic parameters:
- Bacmax: maximum capacity for bacterial growth
- beta: maximum attainable growth rate
- ksyn: synthesis rate of cyclized glutamine from glutamine
- kdim: dimerization rate of two cyclized glutamines to an Indigoidine dimer
- kdegi: degradation rate of indigoidine
In addition, the experimental error for the observables was estimated with 2 error parameters and the initial concentration of the bacteria at t=0 was estimated. Data was otherwise normalized between 0 and 1, thus no scaling and offset parameters were required. In order to keep the model simple, it does not contain glutamine production, the initial glutamine concentration was arbitrarily set to 1. While this does not permit conclusions about absolute indigoidine synthesis rates, comparison of rates between the individual conditions is possible.

Framework
Parameters have to be estimated from experimental data. In order to implement our mathematical model and the wetlab data, we used an open-source software package allowing for comprehensive analysis (D2D Software). With this framework, we were able to calibrate the model and perform robust parameter estimations
Results
We received experimental data from the indigoidine team, who wanted to compare indigoidine synthesis rates between various T domains and PPTases. The model described above was thus fitted individually to each T domain / PPTase combination and simultaneously to all replicates. The data sets could be grouped into two types, those with a significant indigoidine production and those without. Although both types of data sets resulted in seemingly good fits (Fig. 4), identifiability analysis using a profile likelihood exploiting approach
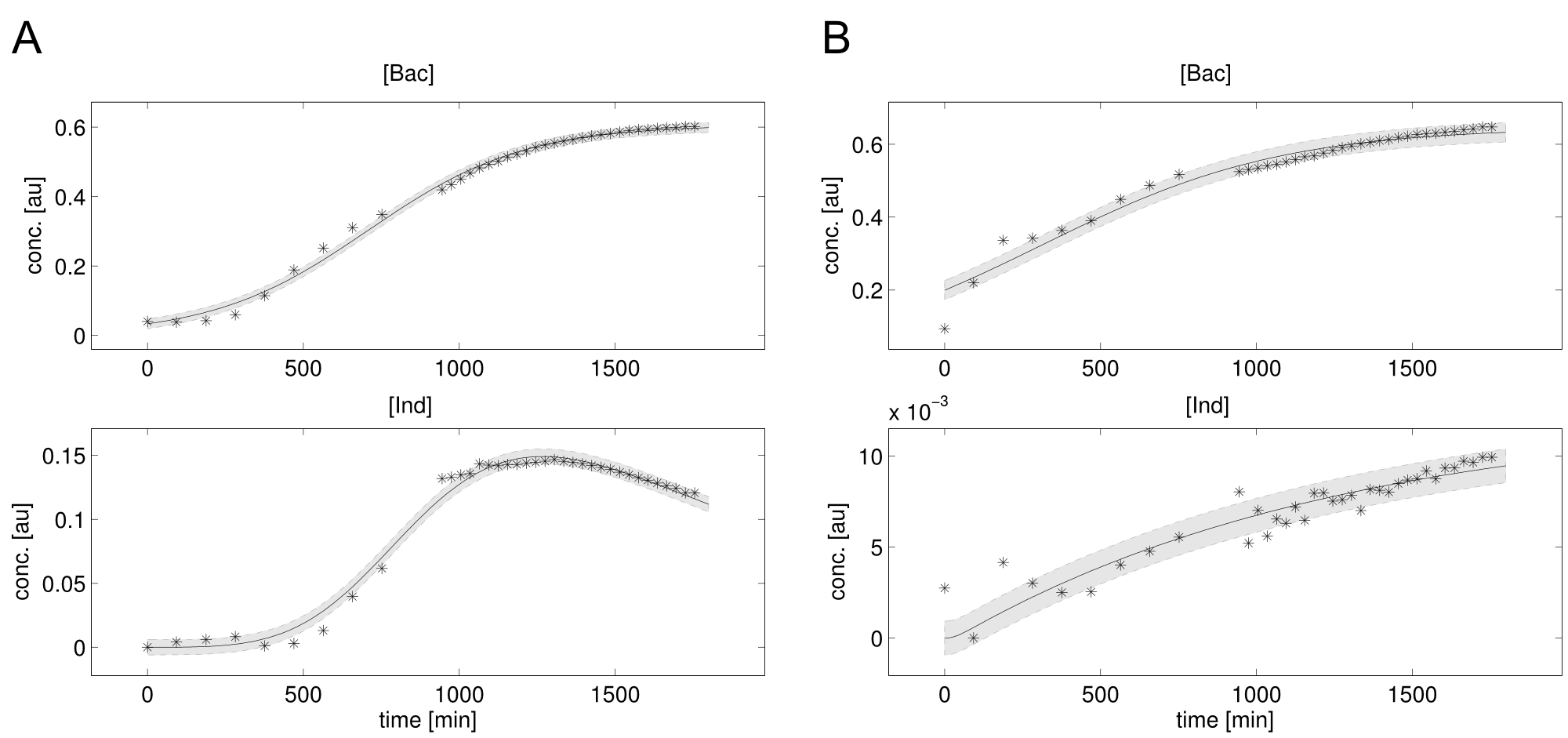
Our mathematical model was able to describe most of our experimental data and was in those cases structurally and practically fully identifiable. We thus challenged the model to deduce additional facts on indigoidine synthesis.
First, we had a look at the parameters that were estimated to describe our experimental data sets. For each parameter estimate, the lower boundary was set to 1e-5 and the upper boundary was set to 1e+5. Initial guesses for parameters during parameter estimations were generated via latin hypercube sampling to ensure broad coverage of all regions in the high-dimensional parameter space
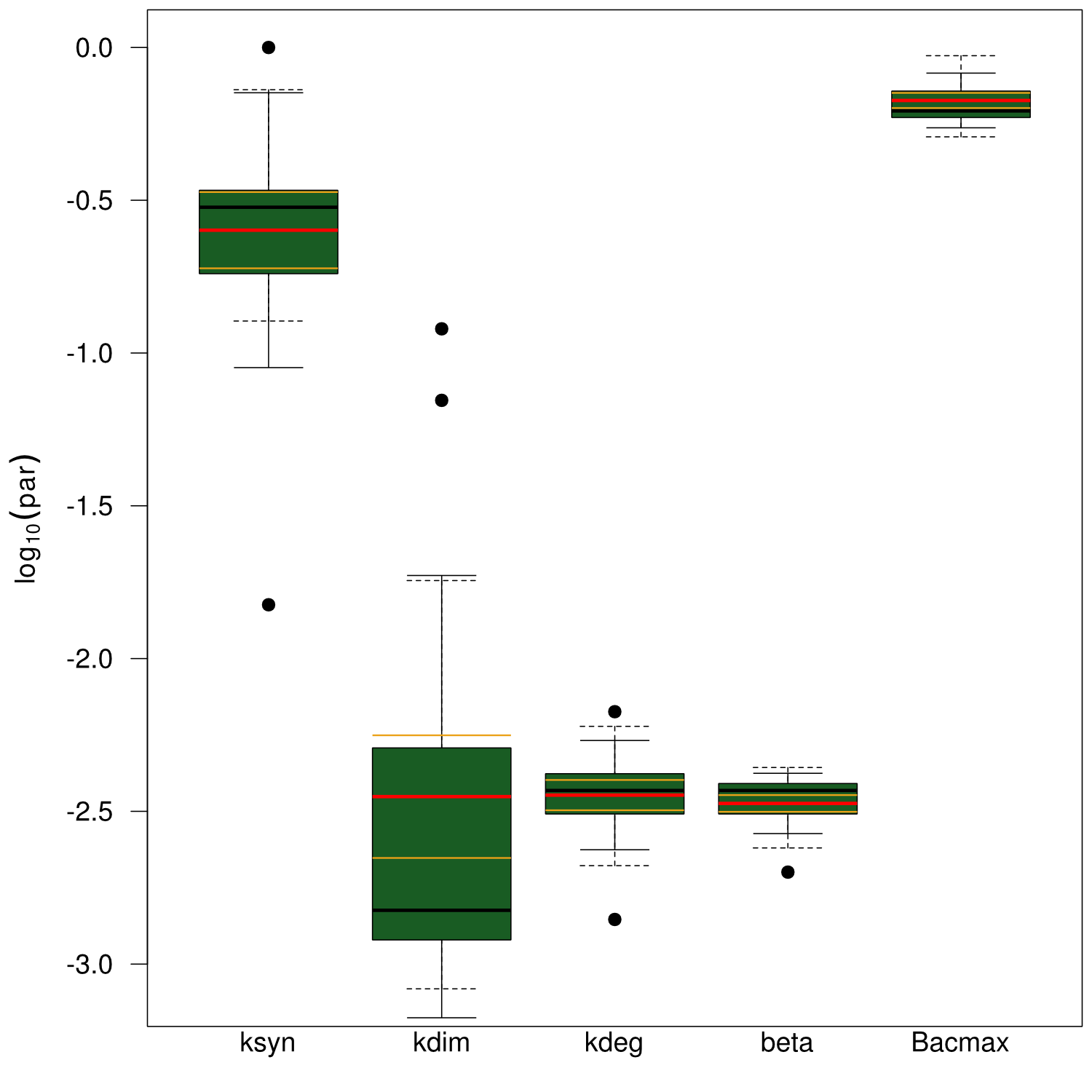
Interestingly, the bacterial growth rate beta and the maximum growth capacity Bacmax were very consistent. The parameters ksyn, kdim and kdegi contributed directly to indogoidine synthesis as it can be inferred from the above mentioned equations \eqref{glu}, \eqref{cglu} and \eqref{ind}. The synthesis rate ksyn characterizes the cyclization of glutamine. The dimerization rate kdim reflects how two cyclized glutamine molecules form one indgoidine molecule. As such, ksyn and kdim represent the efficiency of the T domain of indC. The degradation rate of indigoidine, kdegi, should be independent from the domain structure of the indigoidine synthetase as the stability of the peptide is not affected by the T domains or the PPTases that were tested. The rate did not vary widely and the diverse data sets could still be explained by the mathematical model. At first glance, kdegi seemed less important for our experimentally assessed conditions. To further investigate the role of kdegi for indigoidine production kinetics, we systematically varied this parameter and compared simulation results. The synthesis of indigoidine was clearly affected by variation of kdegi (Fig. 7). The [Ind] trajectory collapsed more than 3-fold increase of the degradation rate. On the contrary, improved peptide stability could yield much more indigoidine. For very low degradation rates (i.e. kdegi < 1e-3), synthesis would not even saturate within the observed time frame.
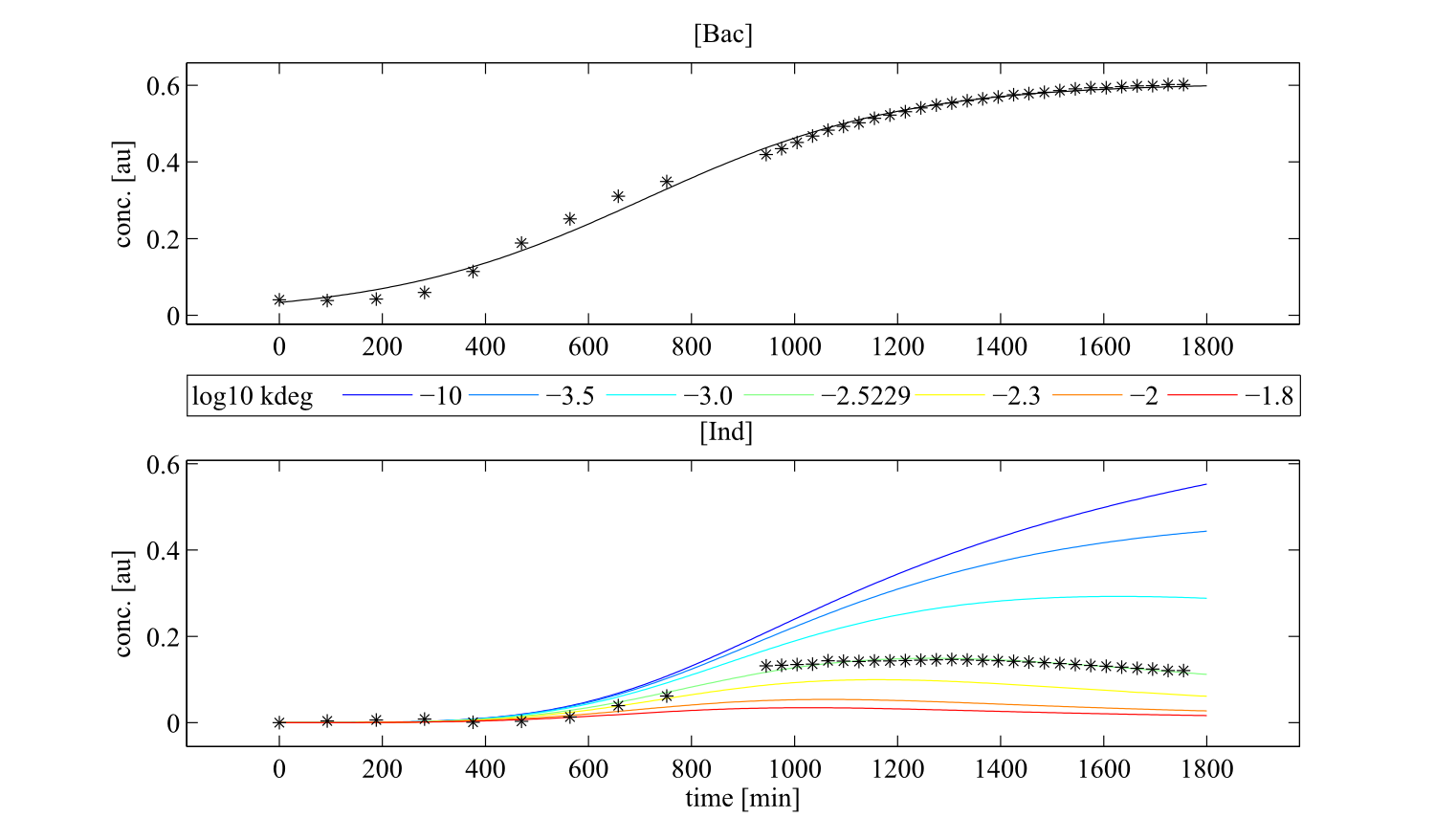
Sensitivity analysis for optimized indigoidine production
To perceive the role of kdegi for indigoidine synthesis, we have varied the parameter over a broad range and observed qualitatively distinct model trajectories. For a more quantitative understanding of how indigoidine yield changes with altering parameters of the system, we conducted a sensitivity analysis
| Parameter | $$\left.\mathrm{[Bac]}\right|_{t=0}$$ | kdegi | kdim | beta | ksyn | Bacmax |
|---|---|---|---|---|---|---|
| $$\frac{\partial\int\!\mathrm{Ind}\,\mathrm{d}t}{\partial p}$$ | 0.784 | -0.7024 | 0.5117 | 0.3338 | 0.2919 | 0.1036 |
The initial concentration of bacteria represented the most crucial parameter for indigoidine production, which was intuitive since the amount of produced indigoidine depends on the amount of bacteria in culture that synthesise the peptide.
The parameter kdegi exhibited a high impact on IntInd but did not vary so much among the experimental conditions. One would assume that the half-life of the peptide is not affected by different T domains or PPTases. Possibly, the arrangement of modules influences peptide stability as inter-modular communication is a precondition for robust peptide assembly
The question is whether those rates could be altered by engineering the NRPS to advanced performance. To answer this question, we performed multiple linear regressions. We regressed the alignment score of the synthetic T domains of the indigoidine synthase with the rates from the respective best fit. The score was calculated by pairwise multiple sequence alignment of the amino acid sequences of the synthetic T domains with the native T domain of the indigoidine synthase as a template. The parameter values were obtained from parameter estimations of our mathematical model that has been calibrated with experimental data as described above. Linear regression of the alignment score on ksyn did only result in a coefficient of correlation of 0.48 while kdim correlated rather well (R2=0.97). This pinpointed the possibility to engineer T domains of NRPSs to optimize kinetic rates in silico for peptide production.
Conclusion and Outlook
We set up a mathematical model for bacterial indigoidine production to showcase the systematic scrutinization of NRP synthesis kinetics. In the course of model calibration with experimental data we could already falsify the hypothesis that indigoidine had an inhibitory effect on growth of the bacteria. The model with such inhibitory terms was not able to describe the experimental data. A reduced model was proven to be fully identifiable via a profile likelihood approach and simulations could reproduce experimental findings. The impact of the different rates on indigoidine production was investigated via sensitivity analysis. We can conclude that yield could be increased when peptide stability is improved and synthesis efficiency is advanced. Linear regression suggests that the dimerization rate of indigoidine could be engineered by editing the T domain sequence. With this, we have learnt valuable lessons on optimizing production of synthetic peptides in silico. Of course, dependency of yield on kinetic parameters does not necessarily scale linearly with peptide length but with these initial trials the way is paved for further analysis.
 "
"