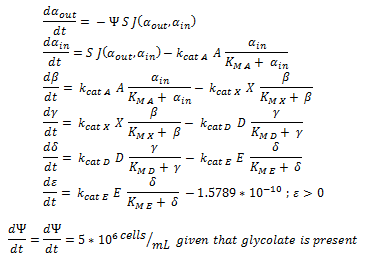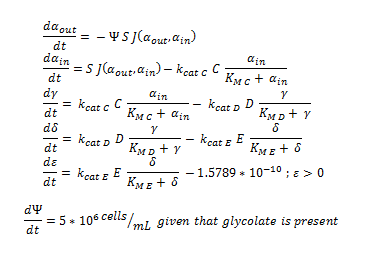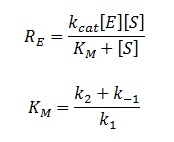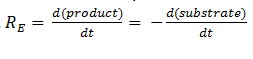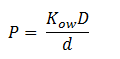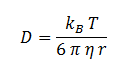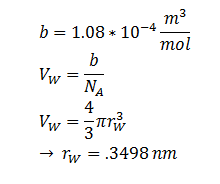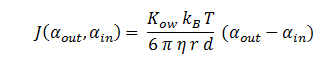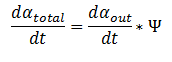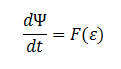Team:SydneyUni Australia/Modelling Principles

From 2013.igem.org

Revision as of 08:43, 18 October 2013 by HZFord (Talk | contribs)

(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)

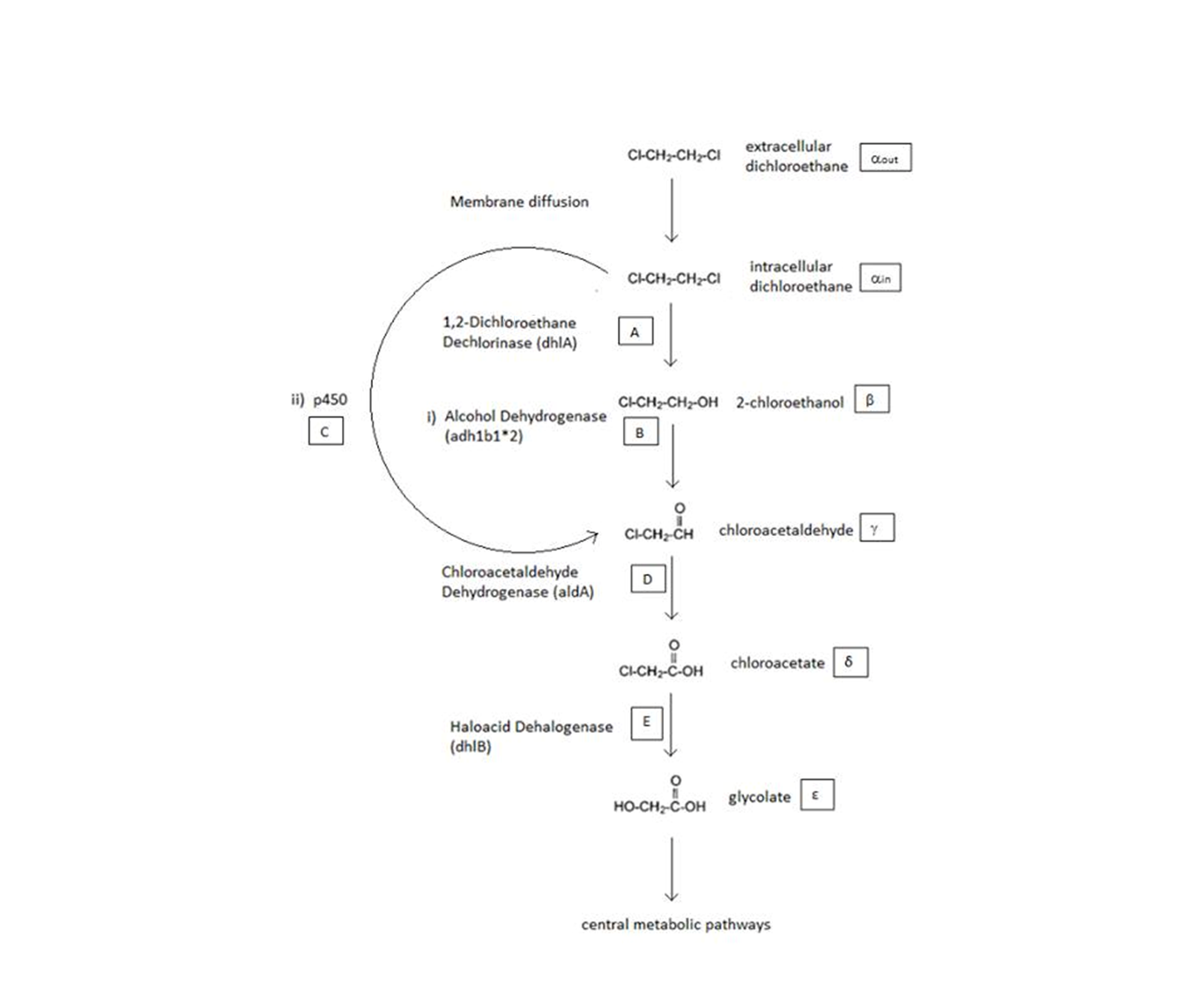
A Schematic of the Engineered Metabolic Pathway:

The above figure is a simplified schematic of the 2 metabolic pathways which are considered. The symbols in squares signify the intracellular concentrations of the associated metabolite (greek letters) or enzyme (capitol English letters). These symbols will be used throughout the analysis.

General Information regarding the Enzymes Involved in the Metabolic Pathway

Enzyme	Gene	Symbol	Constants	Substrate	Product	Ref
1,2-Dichloroethane Dechlorinase	dhlA	A	K_{M A} = 0.53 mM, k_{cat A} = 3.3 s^-1	DCA	2-chloroethanol	[1]
Alcohol Dehydrogenase	Adhlb 1/2*	B	K_{M B} = 0.94 mM, k_{cat B} = 0.0871 s^-1	2-chloroethanol	chloroacetaldehyde	[2]
p450	p450	C	K_{M C} = 7.2 mM, k_{cat C} = 89.8 s^-1	DCA	chloroacetaldehyde	[3]
Chloroacetaldehyde Dehydrogenase	aldA	D	K_{M D} = 0.06mM, k_{cat D} = 0.60 s^-1	chloroacetaldehyde	chloroacetate	[4]
Haloacetate Dehydrogenase	dhlB	E	K_{M E} = 20 mM, k_{cat E} = 25.4 s^-1	chloroacetate	glycolate	[5]

A table that summarises the enzymes that we used in both of the engineered metabolic pathways. The constants presented were (painstakingly) obtained from the literature (referenced).

values based on ethonal as a substrate

ODE Model

Firstly, (and mainly for the mathematical modellers reading this) the overview of the system of ODEs describing the 2 different pathways:

The non-monooxygenase pathway (with dhlA (A) and adh1b1*2 (B)).

The monooxygeanse pathway (with p450 (C)).

The 2 above system of ODEs were used to model 2 things: 1.The rate at which extracellular DCA is removed from solution (given the number of cells in solution) . This is considering the rate at which DCA crosses the plasma membrane (from solution to cytoplasm) of all cells in solution. 2. The rate at which the intracellular concentrations of the metabolic intermediates change over time within a single cell. This considers the relative activities of the enzymes of the metabolic pathway.

The symbols A, B, C, D & E represent the intracellular enzyme concentrations of 1,2-Dichloroethane Dechlorinase, Alcohol Dehydrogenase, Cytochrome p450, Chloroacetaldehyde Dehydrogenase and Haloacetate Dehydrogenase respectively. They have units of mM The symbols α_in, β, γ, δ and ε represent the intracellular concentrations of the metabolic intermediates DCA, 2-chloroethanol, chloroacetaldehyde, chloroacetate and glycolate respectively. They have units mM. α_out represents the extracellular concentration of DCA, ie the concentration of DCA in solution. It has units mM. The symbol Ψ represents the concentration of cells in solution and has units cells/mL.

The function J(α_out,α_in) represents the rate which extracellular DCA moves across the plasma membrane and into the single cell (the flux rate). It is a function of the extra and intracellular concentrations of DCA and has a value of surface area per time m^2/s. The value S represents the average surface area of the cellular membrane of E. coli. By multiplying S by J one achieves the total amount of DCA flowing into a single cell per unit time. The total amount of DCA flowing from solution is achieved by multiplying Ψ by S and J.

Construction of a model for the metabolic pathway

Each line represents how the metabolic intermediate changes over time; this is dictated by the relative rate at which the intermediate is formed vs the rate at which it is used/removed. So, for the metabolic component of the ODE, the rate at which the intracellular concentration of metabolites (β, γ, δ and ε) change over time is purely determined through the relative activity (described by MM equations) of the enzymes creating or removing the metabolite. The rate at which once substrate is removed is directly equal to the rate at which the associated product is created, for instance, the rate at which γ is removed is the rate at which δ is formed. By observing how each intermediate simultaneously acts as a substrate and product, it is easy to see how this process gives rise to a connected system of equations.

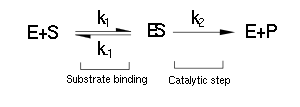
(Luckily) the enzymes of our metabolic pathway are accurately described by MM kinetics and all constants were available in the literature. The system is based on the forward and reverse kinetic rate (k₁ and k_-1 respectively) of substrate-enzyme binding followed by the irreversible catalytic step of product formation (k₂) as depicted in the figure below:

The rate of catalysis for an enzyme is a function of the enzyme and substrate concentration and incorporates the catalytic constant k_cat and the Michalies constant K_M, which are given in most of the literature that involves enzyme kinetics.

The symbol R_E denotes the reaction rate: ie the rate of product formation (which is equal to the rate of substrate removal).

DCA Diffusion Across the Plasma Membrane

The diffusion of DCA across the cell membrane was modelled based on Fick’s first law of diffusion:

Fick’s first law of diffusion is appropriate since 1,2-DCA is non-polar. The law states that the flux, J, of DCA across the membrane is equal to the permeability coefficient, P, times the concentration difference of DCA across the cell membrane. The flux has units has units L² T^-1. The permeability coefficient of DCA is not reported in the literature, but can be estimated through the relation:

Where D is the diffusion constant of DCA across the plasma membrane and d is the length of the membrane. The partition coefficient for DCA across a plasma membrane is not documented, but can be estimated to the octanal-water partition coefficient (K_ow). This constant is the equilibrium ratio of DCA in octanol and water. The diffusion constant, D, is not documented in the literature but can be estimated through the Stokes-Einstein equation based on an estimation of the radius of DCA and viscosity of the cellular membrane.

The Stokes-Einstein equation for determining the diffusion constant D. k_b, T, η & r represent the Boltzmann constant, temperature, viscosity of the membrane and radius of DCA respectively. Here we must assume DCA is spherical. The ‘radius’ of DCA isn’t described in the literature. But the van der Waal constant, b, can be used to calculate the van der Waal volume, V_W, and hence the van der Waal radius, r_W³. Note DCA is not spherical, and this method is used to calculate atoms.

In Summary, the flux across the membrane is:

Summary of Constants

Symbol	Name	Value (units)	Ref
η	Cellular Membrane Viscosity	1.9 kg/m/s	[6]
S	E. coli Membrane Surface Area	6x10^-12 m²	[7]
r	DCA radius	0.3498 nm	[8]
K_ow	Octanol-water Partition Coefficient for DCA	28.2	[9]
d	Length of Cellular Membrane	???	[10]

Extending the System to Cell Cultures

The model can be extended to a homogeneous solution/culture of cells. Let Ψ represent the concentration of the cells in solution. The overall rate of decrease of DCA (α_total) in solution is

By applying this change, the resulting values of α_in,α_out, β, γ & δ represent the metabolite concentration across all cells.

Furthermore the cells are expected to grow due to the production of glycolate (which can be used as a carbon source for growth).

The rate at which E. coli can grow based on the amount of glycolate is not described in the literature. However one will be able to infer the growth as a function of amount of glycolate, ε, in the cell through experimentation.