Team:uOttawa/project
From 2013.igem.org

Background
The Type-I Incoherent Feedforward Loop and Fold-Change Detection
The type-I incoherent feedforward loop (I1-FFL) is a gene network in which protein X activates a gene Z while simultaneously activating the production of a repressor of gene Z, labeled Y.

For this year’s project, we are aiming to construct an I1-FFL that can detect fold-changes in the levels of protein X. In other words, the expression of Z would be reliant on the relative change in X as opposed to absolute values of X. For example, if X changes from an arbitrary concentration of 1 to an arbitrary concentration of 5, the level of expression of gene Z would be exactly the same as that resulting from a change from a concentration of 5 to a concentration of 25 of X (a fold-change by a factor of 5 in both cases).
How Fold-Change Detection is Achieved
This fold-change detection is enabled through the repressor Y. Take the case when activator X, repressor Y, and protein Z each have an arbitrary concentration of 1 in the cell (1:1:1 ratio). If the concentration of X is doubled, the ratio between X and Y now becomes 2:1. X immediately activates Z, but since the repressor Y takes time to fold, it lags behind, and the concentration of Z spikes to 2 due to the activation. When Y folds into its active form and carries out its repressive activity, the concentration of Z returns to its initial concentration of 1. This is because at this point, X and Y return to a 1:1 ratio in the cell. In order for the concentration of Z to reach 2 once again, the X:Y ratio must first return to 2:1 - thus, X has to reach a concentration of 4 before the same output of Z is produced. In this way, fold-change detection is achieved.

Engineering our System
The Design of our Gene Network and the Interactions Between Components
In our proposed design, rtTA will act as our activator (X), Lacl as our repressor (Y), and sfGFP as our reporter protein (Z). Each part is detectable via a different fluorescent protein. A visual representation of our pathway is shown in Figure 3.
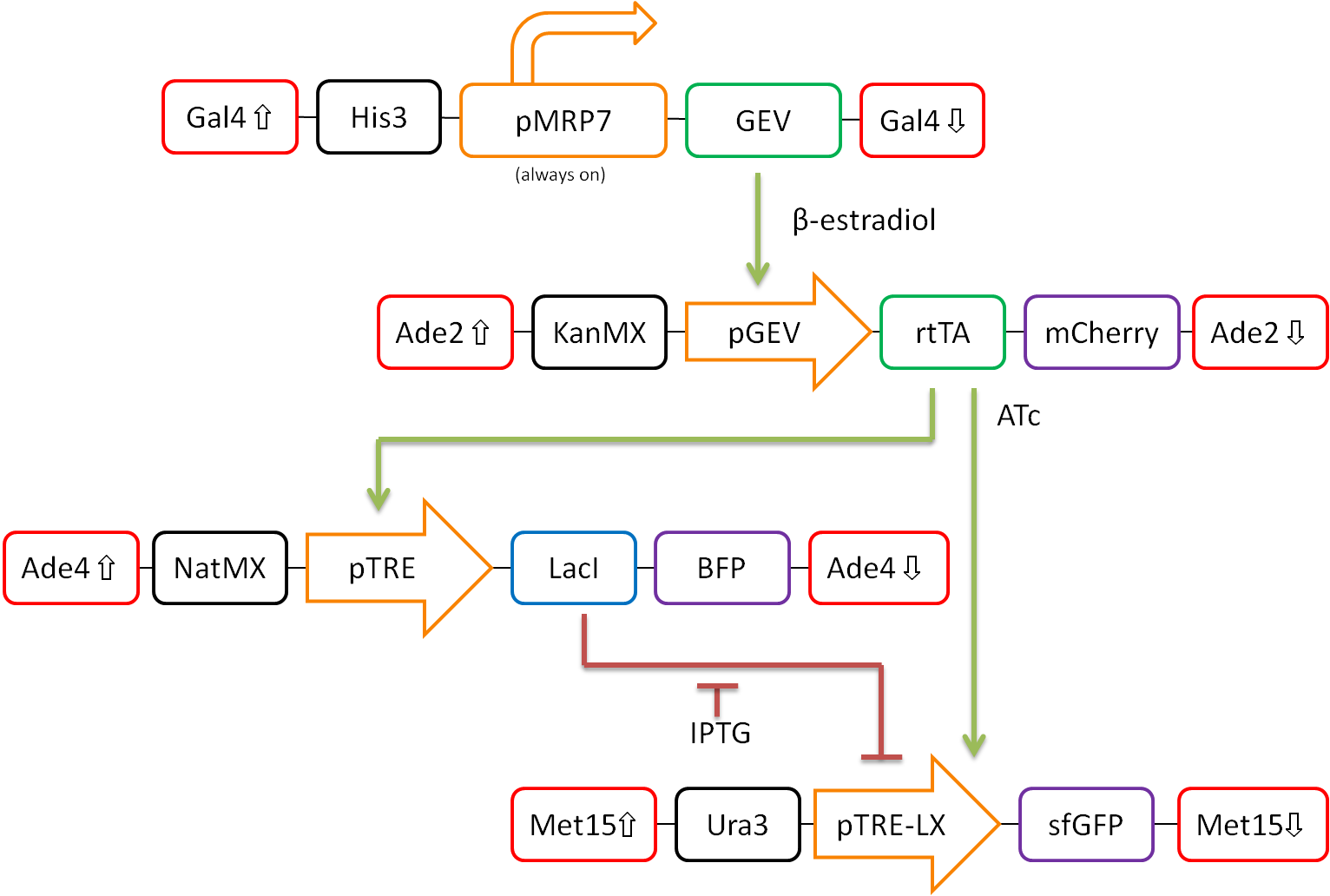
This network design allows for calibration of the network via tunable levels of β-estradiol, allowing for accurate control of the amount of rtTA(X) in the cell. This will allow us to ensure that fold-change detection works as theorized in our network.
Furthermore, activation by rtTA is mediated by varying levels of anhydrotetracycline (ATc), and LacI repression is mediated by varying levels of Isopropyl β-D-1-thiogalactopyranoside (IPTG). These methods of mediation allow for high tunability of the system, and we should be able to find a concentration range of ATc and IPTG at which the system will work as desired.
The system will then be characterized extensively. The fluorescent markers tagged to each component of the network will allow for simple temporal analysis using flow cytometry. This will allow for a high-throughput analysis of the activity of our network.
Potential Applications
A Fold-Change Detection System for Toxic Molecules
Once our system is tuned and is working, it can be modified to act as a fold-change detector for toxic molecules. By replacing the pGEV promoter in front of the rtTA gene with a promoter that is inducible by a toxic molecule, the amount of rtTA produced will be directly correlated to the concentration of the toxic molecule in the cellular environment.

This detector system is advantageous in that it detects fold-changes rather than changes in absolute values, which gives meaning to a signal in reference to the background signal level. This allows for the network to respond only to a signal that rises significantly above the background noise.
Our lab team is currently hard at work.
Move along.
Modeling the Type-I Incoherent Feedforward Loop
The Feedforward loop can be broken down into 3 main steps
1. Toxin will stimulate production of X (rtTA).
2. X (rtTA) stimulates production of both Z (sfGFP) and Y (LacI).
3. Sufficient repression from Y terminates Z (sfGFP) production.
You can take a better look at the system by clicking on the button below!


Equations involved in modeling the biological system
The mathematical model was developed using basic rate formulas of activation and repression as shown in the system of equations above. We then expanded them to include the different parameters required for our model.
These additions are as follows
IPTG concentration to calculate the amount of Y (LacI) repressing Z (sfGFP).
ATC concentration to calculate the amount of X (rtTA) available to bind Y promoter and Z promoter.
Transfer rates of proteins between the cytosol and the nuclei to calculate transfer rates by size of each protein.
The four rate equations for the production of mRNA over time of GEV (1.1), X (rtTA) (2.1), Y (LacI) (3.1) and Z (sfGFP) (4.1) in the nucleus are show below.

The first sets of equations were used to describe the amount of mRNA transcribed. These equations also took into consideration that the mRNA would be transported out of the nuclei. In the model, we assumed that all of the mRNA molecules would be exported to the cytosol. The differential equations representing the variation in mRNA in the cytosol are represented below in equations 1.2, 2.2, 3.2 and 4.2.

Computing the variation and amounts of mRNA in the cytosol over time then allowed us to compute the variation of protein translated. The equations of translation shown below in equations 1.3, 2.3, 3.3, 4.3 represent the variation of protein in the cytosol over time. The translational rates were calculated based on the average translation rate of a ribosome (9.5 base pair per second 12). Here, we assume that the quantity of ribosome is not a limiting factor and that there are no translational regulations involved in the model. The degradation rates are taken from the average degradation rate of protein in yeast14.

Once the amounts of protein calculated, we assumed that they would diffuse at an average rate through the nuclear pore to then affect the transcription of the other genes in the system. The calculations leading to the transfer rates are described in the parameter section under transf. Equations 1.4, 2.4, 3.4 and 4.4 represent the variation of protein present in the nucleus over time.

To have better control on the feed-forward loop system, LacI was regulated with IPTG. Changing the amount of ATC regulated the amount of active rtTA. And the Amount of GEV available to activate production of rtTA is controlled with ß-estradiol. The following equations used to compute the amount of each compound are shown below. These numbers are imputed in the mRNA equations and vary accordingly with the amount of each transcription factors expressed in the ODE system.

Parameters
Some parameters were found in the literature. Others were derived from other known constants as explained below.
Transcription rate
The transcription rate was calculated using the known rate of 2kb per minutes6 which translates to 33.3 nucleotides per second. This rate was then divided by the amount of nucleotides in one mRNA strand. The values are in the parameter table.
Translation rate
The translation rate was calculated using the known rate of 9.5 amino acid per second12. This rate was then divided by the amount of amino acids per protein. The values are in the parameter table.
Transfer rate of protein from the cytosol to the nucleus
The rate of transfer from the cytosol to the nucleus was extrapolated from the formula rate = 0.01*(5000-size of protein in Dalton)-50. This is the multiplied by 119 or the average number of nuclear pores in yeast7. The first equation was determined by assuming that transfer rate of protein 5000 Da takes 0 seconds and a 17000 Da protein takes 120 seconds11.
|
|
GEV |
rtTA |
LacI |
sfGFP |
IPTG |
ß-estradiol |
ATC |
|
Translation rates (mRNA/s) |
0.02088 |
0.01503 |
0.01599 |
0.03991 |
|
|
|
|
n (Hill coefficient) |
1 |
2 |
2 |
- |
2 |
1 |
1 |
|
K |
10^-613 |
5*10^-413 |
10^-10 1 |
- |
5*10^-63 |
10^-94 |
1.56*10^-913 |
|
FullTrans (molecules/second) |
0.02442 |
0.01758 |
0.01870 |
0.04668 |
|
|
|
|
Transf |
0.297 |
0.19993 |
0.2150 |
|
|
|
|
|
Leakage |
1.5 molecule/hour for one promoter |
||||||
References
- http://bionumbers.hms.harvard.edu/bionumber.aspx?&id=100741&ver=0 K of LacI to DNA.
- http://bionumbers.hms.harvard.edu/bionumber.aspx?&id=100743&ver=0&trm=laci K of IPTG to LacI.
- http://pubs.acs.org/doi/pdf/10.1021/jp308930c K of IPTG to LacI.
- http://www.rcsb.org/pdb/explore/explore.do?structureId=1ORK
- http://www.ncbi.nlm.nih.gov/pmc/articles/PMC373162/ Time division of yeast
- http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3154325/pdf/nihms314191.pdf Fully induced transcription
- http://bionumbers.hms.harvard.edu/bionumber.aspx?&id=101395&ver=1&trm=pore%20yeast number of pores
- https://2009.igem.org/Team:PKU_Beijing/Modeling/ODE calculation of rate
- http://www.ncbi.nlm.nih.gov/pmc/articles/PMC373162/ Time division of yeast
- http://www.nature.com/nbt/journal/v30/n7/pdf/nbt.2281.pdf Half life of sfGFP
- http://www.ncbi.nlm.nih.gov/books/NBK26932/ speed of pore
- http://download.cell.com/pdf/PIIS0092867413006557.pdf?intermediate=true Rate of translation
- Approximated to adapt the model
- Dmitry Nevozhaya, Rhys M. Adamsa, Kevin F. Murphyb, Kresˇimir Josic, and Ga bor Bala zsia, Negative autoregulation linearizes the dose–response and suppresses the heterogeneity of gene expression, www.pnas.org/cgi/doi/10.1073/pnas.0809901106
 "
"







