Team:Exeter/Modelling
From 2013.igem.org
Introduction
Our model predicts how the absorption spectrum of a modified E. coli changes over time in response to a given incident light spectrum. It is used to estimate key properties of our system such as stability, development time of image, the balance of colours and has three steps to its operation.
The model is split into three sections. The first part calculates the reaction of each sensor species to a given incident light spectrum. The second is the heart of the model and it simulates the biochemistry of our designed pathways according to how the sensors respond to the light. The third and final part takes the data from the simulation and plots a surface showing how the absorption spectrum of a cell changes with time.
Currently the model is based on results from literature and theoretical conjecture as experimental results are not available. The motivation for the model was to numerically characterize our bio-bricks for future use and to help us create the first colour coliroid. With experimental results the model could readily be updated to fulfill its original mandate.
The Team
| | | |
Modelling Software
The model uses two programs; [http://www.mathworks.co.uk/products/matlab/ MATLAB®] and KaSiM. Together they provide the necessary tools to create an accurate model of our system.
KaSiM and Kappa
KaSiM is a [http://en.wikipedia.org/wiki/Stochastic stochastic] simulator that executes files written in [http://www.kappalanguage.org/ Kappa]. Kappa is a rule based modelling language for protein interaction networks.
MATLAB®
MATLAB® is a high-level language and interactive environment for numerical computation, visualization, and programming. It can be used to analyze data, develop algorithms, and create models and applications.
The model
The model describes the absorption spectrum of the cell as a function of time and a given time invariant incident light spectrum. This is achieved by calculating the effect of the known light input on the individual light sensitive proteins. This information is then fed into a stochastic simulation of the biological pathways that computes how the population of sensors and pigments vary over time. The total absorption spectrum over time is given by the sum of the product of every protein's population and the corresponding absorption spectrum of the protein. In this section each of these steps in considered in the following subsections.
It will be helpful to read the theory page and the modelling software section of this page before reading further as an understanding of the biological pathways and software is important for understanding the
Sensor activation rate
The rule for each sensor is that it is either on or off. In the on state it catalyses the phosphorylation of the primary intermediate and in the off state it does not. Activation by light either turns a sensor on or off depending on the sensor species; the red and blue light sensors are switched off when activated while the green light sensor is switched on when activated. The activation rate is the forward rate of the rule that governs the state of a sensor. Its counterpart, the deactivation rate is the backward rate of the same rule.
The activation rate is calculated as the integral over all space of the product of the sensor's frequency response with the frequency spectrum of the incident light.
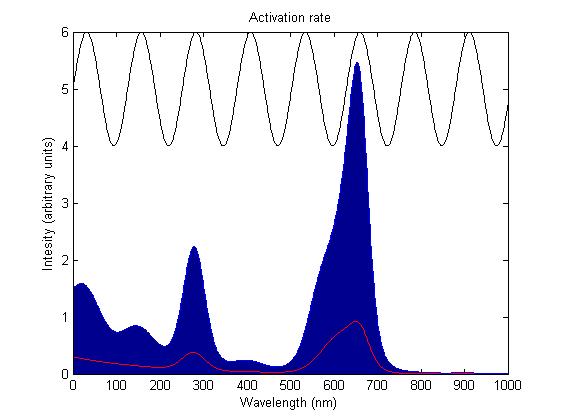
This has two important implications. Firstly it means that the sensor will not be activated by light that has no overlap between its spectrum and the frequency response of the sensor. Secondly there will be a saturation point at high intensity light where increasing the intensity will not appreciably affect the system as the activation rate will dominate the deactivation rate. Causing the sensors to be effectively permanently activated. These characteristics are faithful to the light sensitive proteins we are using and that is why we are using this method.
Kappa model
This subsection will explain the kappa model. How it works, the justification for its use,
Absorption spectrum
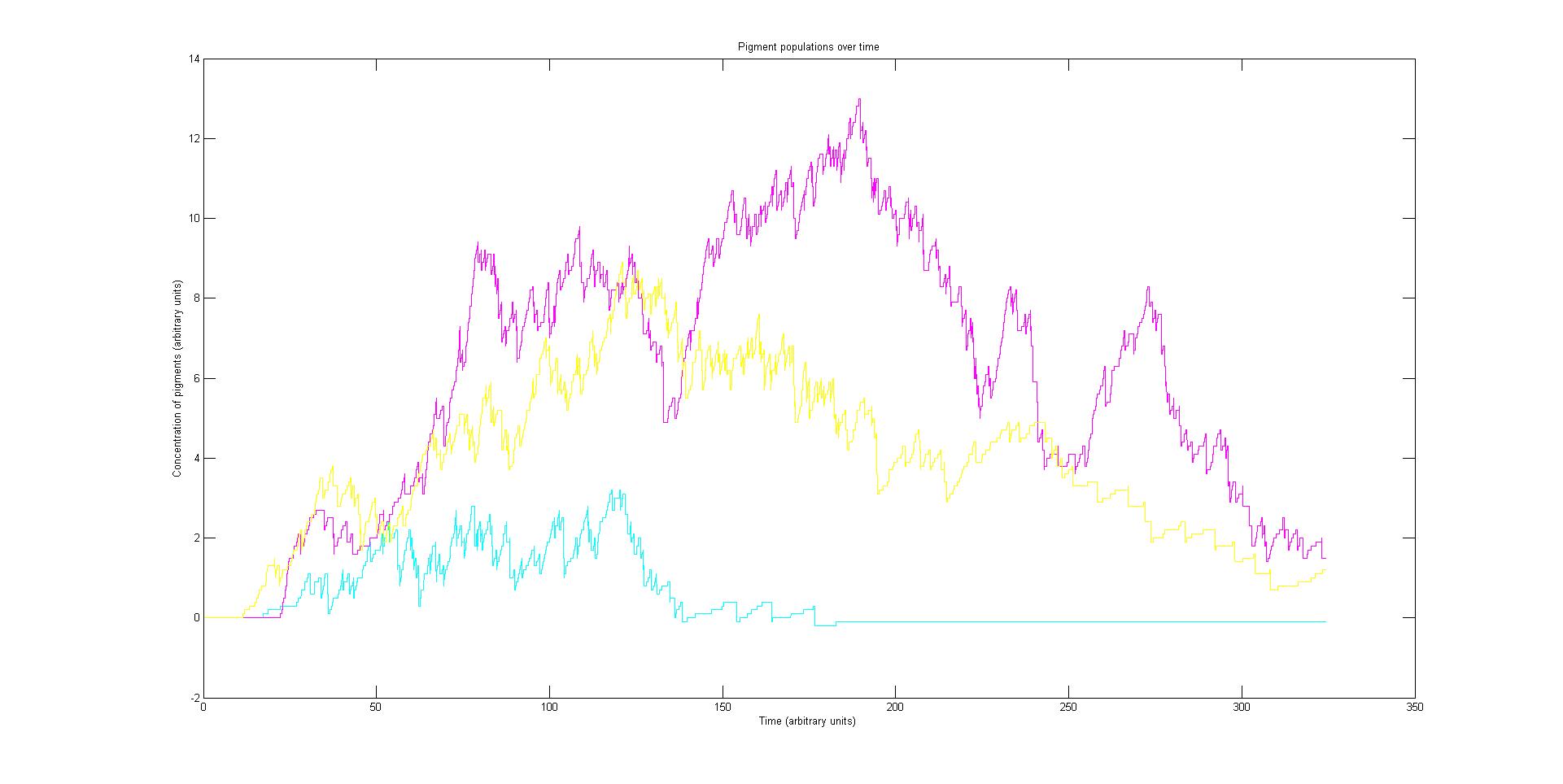
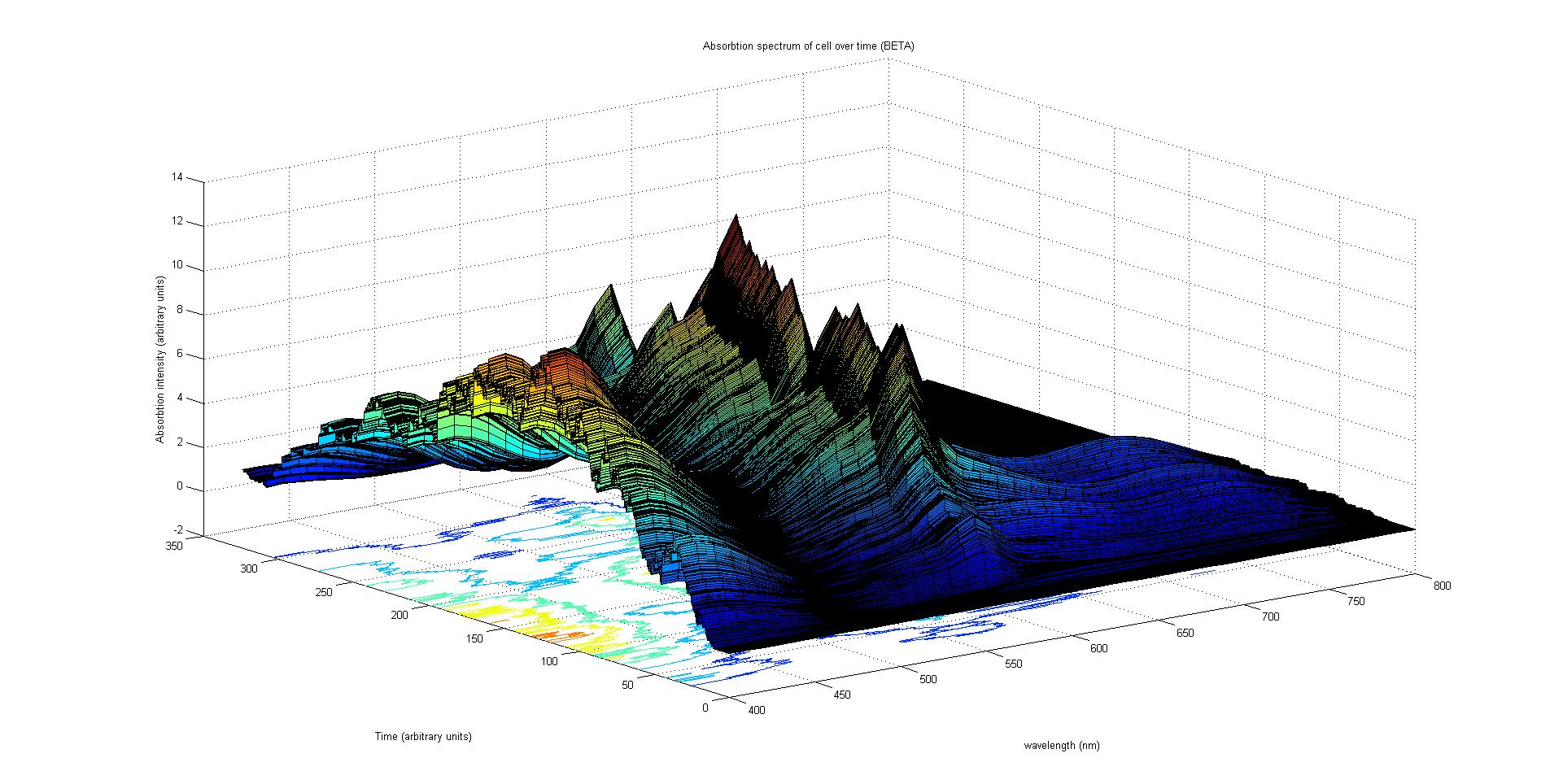
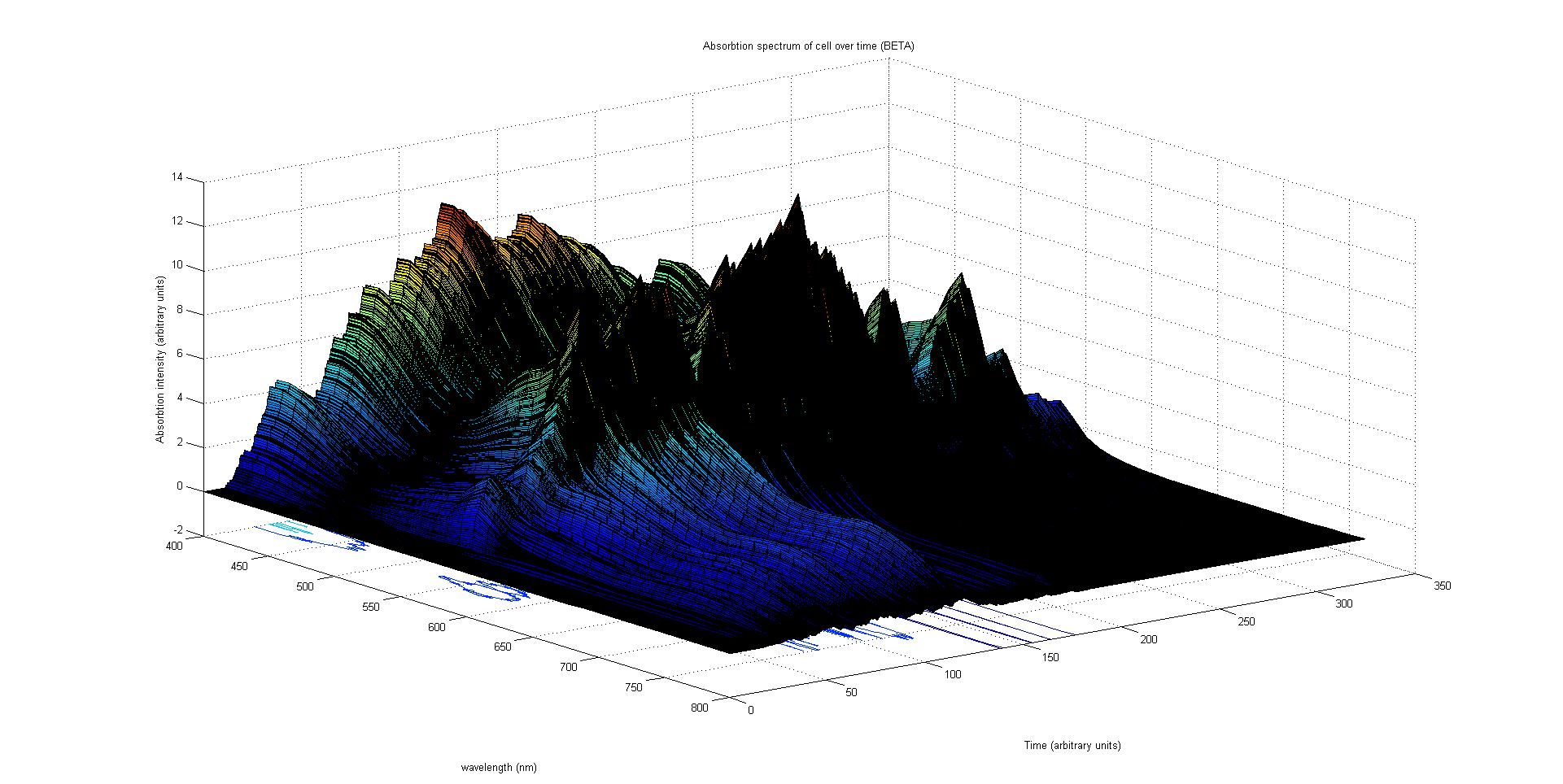
Each protein species has an associated absorption spectrum. This multiplied by the population of the protein at a point in time gives the contribution of that protein to the total absorption spectrum of the cell at that moment. The sum of the contributions from each protein plus the absorption spectrum of the background cell gives the total absorption spectrum of the cell at that moment. This calculation repeated for every time step gives the total absorption of the cell over time.
The absorption spectrum over time is plotted as a surface of intensity as a function of time and frequency.
The absorption spectrum at a point in time tells us what colour and tone the cell will be at that moment. Over time it shows us how the mix of colours change as the image develops, how long it takes to reach an equilibrium, the moment of greatest contrast and many other important features.
It will also reveal how the expression of a gene is controlled by each light sensitive pathway. Something which has implications for future projects.
Results
This section will list in detail the results of our model
Preliminary results suggest that the mix of colours in an individual e.coli is very unpredicatable. But the average for a cohort of cells is more predicatable.
Analysis
This section will contain what the data means
Conclusions
This section will contain our conclusions about the model
Future
This section will contain our opinions about the future of the model
 "
"