Team:Valencia Biocampus/Modeling
From 2013.igem.org
Modeling
The main goal of our modeling project is to accurately predict the behavior of our system in several issues, from the mounting of bacteria on C. elegans to the performance of our worms reaching the place of interest. In order to do that, we use several modeling techniques.
The movement of C. elegans in the presence of a chemoattractant in order to carry our bacteria to that source is the main issue of our project, so we consider modeling this aspect and employing it as scaffold for the whole modeling project. Several layers show up that it must be modeled in different ways. In our approach, we mathematically describe each layer, from the simplest to the most complex, integrating each one.
The workflow in the C. elegans movement is the following:
| Single Worm Behavior | Single Worm Chemotaxis | Group Behavior | Wormboys in action | System performance | ||
|---|---|---|---|---|---|---|
| Considerations | Chemoattractant | |||||
| Bacteria | ||||||
| Modeling approach | Random Walk | Biased Random Walk | Partial Differential Equations | Partial Differential Equations | Ordinary Differential Equations | |
The model is improved adding the data obtained from the experiments in order to achieve a holistic model which can predict the distribution of our worms, the kinetics of the present bacteria and the concentration of the substrate in each moment.
Biobricks modeling
In this section, clumping and PHA production are modeled and fitted to a equation. These things will be considered in other sections.
Clumping
PHA production
C. elegans behavior
In order to understand the system as a whole, we started with the simplest case, so our first study is based on the behavior of a single worm, initially in the absence of chemoattractant and later adding it.
Our first approach consists in the study of a single worm in a surface without chemoattractant, under this condition it is observed that a C. elegans moves randomly, this is defined as a Random Walk.
Random Walk is the mathematical formalization of a trajectory that consists of taking successive random steps. We ran several simulations in Scilab and C++, in order to represent a single C. elegans moving this way in the absence of attractants.
Random walks are used to describe the trajectories of many motile animals and microorganisms. They are useful for both qualitative and quantitative descriptions of the behavior of such creatures. In our case a single C. elegans was simulated as a point: $(x_t, y_t)$
At each instant $t$ in the simulation, step length $l_t$ and direction $\theta_t$ the equations are the following:
$$l_t = \Delta t\;\nu_t$$
$$\theta_t = \theta_{t-1} + \Delta t \left(\frac{d\theta_t}{dt} + \delta\right) $$
Where $\Delta t$ is the duration of the time step, $\nu_t$ is the instantaneous speed, $\frac{d\theta_t}{dt}$ $(= \dot{\theta_t})$ is the instantaneous turning rate (using the convention that $\frac{d\theta_t}{dt}$$ > 0$ is a right turn and $\frac{d\theta_t}{dt}$$ < 0$ is a left turn) and $\delta$ is the turning bias.
The values of these variables were taken randomly from different gaussian distributions, that we identified by sampling but also obtained from some papers:
$\nu_t$: normal distribution with $\sigma = 0.0152\;cm/s$ and $\mu = 0.00702\;cm/s$
$\dot{\theta_t}$: normal distribution with $\sigma = 0.0150273\;rad/s$ and $\mu = 0.6789331\;rad/s$
$\delta$: normal distribution with $\sigma = 0.0076969\;rad/s$ and $\mu = 0.0370010\;rad/s$
Simulations were performed in Scilab and C++, proceeding as described in (Pierce-Shimomura et al., 1999). We contacted the authors but they could not provide us with the code, so we developed our own script based on the article, obtaining similar results:
You can also simulate C.elegans random walk in our Simuelegans online application
Simulated with our own software SimuElegans.
Please note that the actual movements of C. elegans are much slower and thus the simulation in this video is accelerated for convenience.
In these simulations we considered $\Delta t = 1\;s$, but actually we simulated it every $0.01\;s$, so its $\frac{1\;s}{0.01\;s} = 100$ times accelerated.
Chemotaxis of a single worm
However, we are interested in the movement of the nematode in a gradient of chemoattractant.
Studies revealed that the behavior of E. coli during chemotaxis is remarkably similar to the behavior of a single C. elegans in the presence of a chemotactic source (Bargmann, 2006), a mechanism called the pirouette model in C. elegans (Pierce-Shimomura et al., 1999) and the biased random walk in bacteria (Berg, 1993; Berg, 1975). The basis of these models is a strategy that uses a short-term memory of attractant concentration to decide whether to maintain the current direction of movement or to change to a new one.
Following this model, we defined the turning rate as a function of $\frac{\partial [C]}{\partial t}$. Where $[C]$ is the concentration ($[\;]$) of chemoattracant ($C$). Simulations were performed as expected, showing a bias in the random walk:
You can also simulate C.elegans chemotaxis in our Simuelegans online application
Simulated with our own software SimuElegans.
Chemotaxis of a single worm consuming attractant
As a last step of the study of a single worm, we decided to modelize the most realistic behavior. This behavior happens when, in addition to moving randomly but biased toward the gradient of chemoattractant, we consider the fact that it is constantly consuming its “food”, so these gradients will not be any more constants in time.
In order to implement this model, we realized that was impossible to study still considering the space as an attractant function, cause it changes its shape in every time step, and it made simulations really slow (maybe, days of computation). So, we meshed the space, and gave every point a different weight, depending on time: that was the starting of the matrix and approximated (numerical) calculations. What we obtained was close to have relevant impacts in the course of our project, because we could interfere in the C. elegans path, and not only in its final position, making it moving from one source of chemoattractant to another:
Simulated using Scilab
Note that this simulation has been speeded 600%.
Moreover, these numerical methods opened our eyes to study their movement as a whole, with partial differential equations.
Bargmann CI (2006) Chemosensation in C. elegans. Wormbook
Berg HC (1993) Random walks in biology. Princeton, NJ: Princeton UP.
Pierce-Shimomura JT, Morse TM, Lockery SR (1999) The Fundamental Role of Pirouettes in C. elegans Chemotaxis. The journal of Neuroscience, 19(21):9557-9569
Group behavior
In practice, a single C. elegans is not employed to perform the task but a group of worms. In this case, the random walk equations obtained for a single worm behavior can be transformed into partial differential equations (PDEs) to depict the distribution of the population, as the ones describing a diffusion process (Click here for a mathematical demonstration of macroscopic RW as a diffusion process)
However, in our case we face a diffusion system with drift, in which the last term arises from the biased movement of C. elegans. To obtain a PDE that reflects this behavior, we employed difference equations using Taylor series and apropiate limits (Click here for a mathematical demonstration of C. elegans chemotactic behavior using PDEs from biased random walk)
The equation is the following:
$$\frac{\partial [C]}{\partial t} = D\;\nabla^2[C] - \nabla\cdot(\overrightarrow{\nu}\;[C]) $$
PDEs. Parameters, as diffusion coefficient (D) or drift force (b) can be calculated from (Pierce-Shimomura, 1999)
Once obtanied the equation that governs our system, we proceed to study if it works correctly for our purpose. However, analytical solutions for this equation are known for few ideal cases. For example, for a monodimensional bistable potential the stationary state is the following (Okopinska, 2002):
$$ P_{ss}=\mathscr{N}^{-1} e^{\left(-V(x)/D\right)}$$ where $ \mathscr{N} $ is the normalization constant.
Add picture
As seen, our system, theoretically can work as expected, depending on the shape of the chemoattractant only. This is a great result because it shows our worms are capable of reaching each region.
Finally, our final goal in this section is predicting temporal and spatial behaviour in two dimensions for non-ideal problems. In this case, numerical methods is the only way to solve the system.
For the 2-dimensional case, $[C] = [C(x, y, t)]$ is the concentration of C. elegans at a given instant $t$ and at a given point $(x, y)$, $D$ is the diffusion coefficient and $\overrightarrow{\nu}$ is the attraction field for the C. elegans, which basically stands for its velocity. This expression naturally expands to:
$$\frac{\partial [C]}{\partial t} = D \; \left(\frac{\partial^2 [C]}{\partial x^2} + \frac{\partial^2 [C]}{\partial y^2}\right) - \left(\frac{\partial\nu_x}{dx}[C] + \nu_x\frac{\partial [C]}{\partial x} + \frac{\partial\nu_y}{dy}[C] + \nu_y\frac{\partial [C]}{\partial y}\right) $$
We first started by building up an explicit finite difference method, this is numerically fast but it is prone to instabilities in the solutions. Therefore, we decided to develop a Crank-Nicolson method which is unconditionally stable, thus being suitable to carry out parameter identification of a model. Nevertheless, it has the drawback of being numerically more intensive, because a set of algebraic equations must be solved in each iteration (Click here for a mathematical explanation of Crank-Nicolson method).
Now, we can predict the behavior of a set of worms in presence of a chemoatractant. Simulations were run using Scilab:
Add simulation
Proof for the Group Behavior Model starting from a Random Walk Model
Considerations for the Random Walk:
- Step lenghts ($l_t$) in the order of a pixel in size. That implies, $ \Delta t $ as small as possible.
-
Perfect Random Walk, with uniform probabilistic distributions either for $ v_t $, $\dot{\theta_t}$ and $\delta$.
Discretizing the whole space into pixels, and assuming, the worm can, either occupy one or not, we can assure that, at each time step, it can only move in four different directions: up, down, right or left from its position. As we considered that each random variable follows an uniform probabilistic distribution, it is equipossible to move in any of these directions, with a probability of $ \frac{1}{4} $ each.
Now, we can compute, the probability that the worm is at position $(x_m,y_m)$ at the iteration $n+1$ as follows:
$$ P_{n+1}(x_m,y_m)\;=\;\frac{1}{4}\;\left(P_{n}(x_m,y_{m+1}) + P_{n}(x_{m+1},y_m) + P_{n}(x_m,y_{m-1}) + P_{n}(x_{m-1},y_m)\right) $$
If we now subtract $ P_{n}(x_m,y_m) $ from both sides:
$$ P_{n+1}(x_m,y_m) - P_{n}(x_m,y_m)\;=\;\frac{1}{4}\;\left(P_{n}(x_m,y_{m+1}) + P_{n}(x_{m+1},y_m) + P_{n}(x_m,y_{m-1}) + P_{n}(x_{m-1},y_m) - 4\;P_{n}(x_m,y_m)\right) $$ $$ P_{n+1}(x_m,y_m) - P_{n}(x_m,y_m)\;=\;\frac{1}{4}\;\left(P_{n}(x_{m+1},y_m) - 2\;P_{n}(x_m,y_m) + P_{n}(x_{m-1},y_m) + P_{n}(x_m,y_{m+1}) - 2\;P_{n}(x_m,y_m) + P_{n}(x_m,y_{m-1})\right) $$
Multiplying and dividing by $q$ (time step) and $h^2$ (space step squared) we then get:
$$ \frac{P_{n+1}(x_m,y_m) - P_{n}(x_m,y_m)}{q}\;=\;\frac{h^2}{4\;q}\;\left(\frac{P_{n}(x_{m+1},y_m) - 2\;P_{n}(x_m,y_m) + P_{n}(x_{m-1},y_m)}{h^2} + \frac{P_{n}(x_m,y_{m+1}) - 2\;P_{n}(x_m,y_m) + P_{n}(x_m,y_{m-1})}{h^2}\right) $$
And, defining the constant $D\;=\;\frac{h^2}{4\;q}$:
$$ \frac{P_{n+1}(x_m,y_m) - P_{n}(x_m,y_m)}{q}\;=\;D\;\left(\frac{P_{n}(x_{m+1},y_m) - 2\;P_{n}(x_m,y_m) + P_{n}(x_{m-1},y_m)}{h^2} + \frac{P_{n}(x_m,y_{m+1}) - 2\;P_{n}(x_m,y_m) + P_{n}(x_m,y_{m-1})}{h^2}\right) $$
That can be approximated as a Diffusion Equation, by recalling the definition for the first and second derivates:
$$\frac{\partial P}{\partial t} = D \; \left(\frac{\partial^2 P}{\partial x^2} + \frac{\partial^2 P}{\partial y^2}\right) $$

Okopinska A. (2002) Fokker-Planck equation for bistable potential in the optimized expansion. Physical review E, Volume 65, 062101
System performance
All this modeling part was made to track a set of worms in a given soil. This can be used to compare our system, a non-stirred solid bioreactor, with a conventional stirred liquid bioreactor.
Modelling this part is difficult because there are a lot of factors involved. Therefore, asumptions must be made. Our first approach is the study of the stationary state in both systems: In a stirred bioreactor, the concentration of both bacteria and substrate are constant whereas in a non-stirred one exists a determinated distribution. For the concentration distribution in the non-stirred bioreactor is gaussian and the bacteria distribution (consecuence of the attraction of C. elegans for the substrate) is given by the stationary state distribution for an one-dimensional case.
The pictures are graphical examples of both situations: Stirred case (left) and non-stirred (rigth). Substrate is shown in purple, bacteria in blue, and the relation between them in grey. The total concentration is the area below the curve.
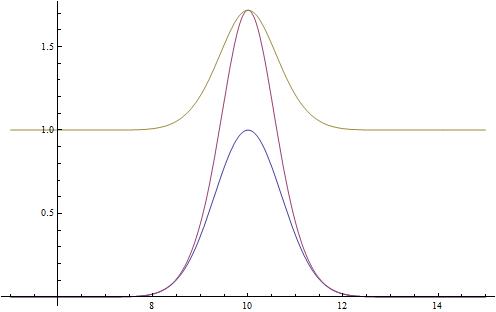
As can be seen, a
 "
"


