Team:HIT-Harbin/Modeling
From 2013.igem.org
| Home | Team | Official Team Profile | Project | Parts Submitted to the Registry | Modeling | Notebook | Safety | Human practices | Attributions |
|---|
Before experiment, a mathematical model is developed to describe our system and make a prediction about our following experiment. Our model is based on the following assumption.
(1) Transcription follows Hill equation, other reactions follows mass action principle and saturation kinetics.
(2) Parameter values are partly found on current publications[1,2] and partly guess in a reasonable way.
(3) The amount of protein binding to promoter is negligible because the amount of protein binding to promoter is trace compared to the total amount of the protein
Model of AND gate

Figure 1 : A Schematic of the Biological Andgate
As described before, HrpS binds to HrpR forming a complex HrpRS. HrpRS then binds to promoter hrpL triggering transcription of the downstream gene. We use two inducible promoters--the isopropylthiogalactoside (IPTG)-inducible Plac and the arabinose-inducible PBAD as the AND gate inputs. A quantitative dynamic model based on protein and protein-promoter interactions for the hrp gene regulatory is described below:
1 Transcription of hrpR and hrpS mRNA
A transcription function named Hill function[3] was used to explain how IPTG, Arabinose and HrpRS influence the promoters. The Hill function and its curve are


Figure 2 : Example of regulation functions (a)Hill function;(b)Step function;(c)logoid function
θj is the threshold for the regulatory influence of the xj on a target gene, m is the steepness parameter. h+ explain the positive regulation on the target gene, while h- is the negative regulation function.
IPTG binds to promoter Plac and trigger the transcription of hrpR_mRNA at a maximum rate constant vmr,

while hrpR_mRNA degrade at a rate constant Drnar, so the dynamic change for hrpR_mRNA is

Similarly, we get the reaction for PBAD, they are


2 Translation of HrpR and HrpS protein
To simplify our model, we made some assumption
(1) the level of translation product is assumed to be proportional to mRNA levels
(2) There is no delay in synthesis of either component or delay because of protein transportation
HrpR and HrpS are synthesized at the rate constants Kr and Ks respectively, and degrade at the rate constant Dr and Ds.

The net forming rate of HrpR and HrpS are

3 Interaction between protein HrpRS and promoter hrpL
HrpR and HrpS binding rate constant is define as Krs, and their dissociation rate constant is K_rs. Complex HrpRS degrade at a rate constant Drs

The net forming rate of HrpRS is

Activating for the promoter hrpL is like Plac and PBAD

Promoter hrpL trigger the transcription of our target protein. Ko and Do denote the synthetic and degradation rate constant for output protein.
The whole model for the hrp AND gate are summarize below

Simulation Result1
Firstly, we test the model when n=1(in one cell). Supposing Kt=Ko=Kr=Ks=30,(Kt, Ko, Kr, Ks is the parameters connected to RBS strength. In our model we imagine that K=3 denote weak RBS, K=30 denote middle RBS, K=60 denote strong RBS. ) Varying IPTG and Arab, we’ve got the output response for the inputs.

Figure 3 : Simulation Results of hrpLANDgate
As shown in figure 3, when IPTG or Arabinose is low the output response is stay at a low level. Only when both inputs are high, is the output reaching high level.
Model of proportional amplifier
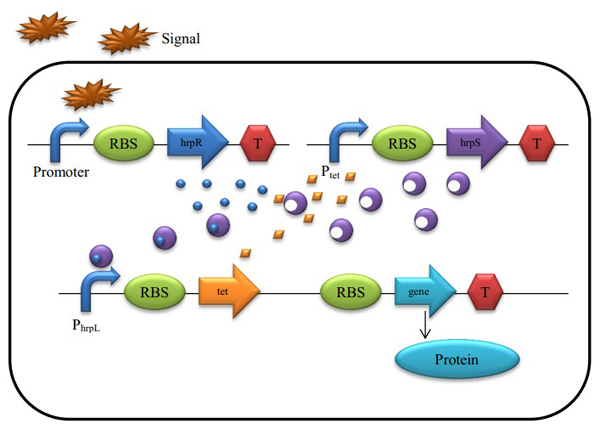 Figure 4 : A Schematic of the Biological Proportional Operational MU-circuit
Figure 4 : A Schematic of the Biological Proportional Operational MU-circuit
Based on the hrp AND gate, we changed the promoter Plac into PtetR which is constitutively on and inhibited by the tetR protein, and add a tetR protein generator to the promoter hrpL’s downstream. Because tetR and output are triggered by the same promoter, they share the same mRNA.

the reaction rate is

Protein tetR have a negative effect on the PtetR promoter, so the hrpS transcription rate under promoter PtetR is

The whole model for the proportional amplifier is summarize below

Simulation Results 2
We test the output response changing with IPTG, when given different combination of RBS strength. To reduced simulation times, Taguchi Design is used in our model. And if possible, we would put it into wet experiment. Taguchi Design table for Ko, Kt, Kr, Ks is given in table1
Table 1 : Experiment for Taguchi Design

Then, we got a series steady state data of input and output and plot them together. Results is shown in figure 5

Figure 5 : Simulation Results for Output Response VS IPTG input
Figure 5 demonstrate that (Ko=3, kt=3, Kr=3, Ks=3), (Ko=30, Kt=60, Kr=3, Ks=30) and (Ko=60, Kt=30, Kr=3, Ks=60) present a better linear relationship between input and output than other experiments. Linear regression is used to describe the relationship between input IPTG concentration and output response.
Table 2 : Linear Regression of Simulation Result for Experiment 2, 3, 6

Here we invented a coefficient m,m=b/a,where b is the concentration range of linear area between output response and IPTG,and a is the whole range of IPTG concentration.

Figure 6 : Effect Plot for m
In figure 6, we found that (Ko=60, Kt=3 or 30, Kr=3, Ks=60) can make the linear range maximum. It means experiment 6 is the best choice of RBS combination.
Parameters and variables are described in the following table
Table 3 : Parameters used in the Model

Table 4 : Variables used in the Model

Table 5 : States used in the Model

Table 6 : Observation used in the Model

PS : Parameters are constants in our model. Variables are what we controlled in one experiment.States are dependent variable changing in one experiment. Observation is our target output
Reference
[1] Baojun Wang. The Design and Construction of a Set of Modular Synthetic BioLogic Devices for Programming Cells. IFMBE 2009
[2] Baojun Wang et al. Engineering modular and orthogonal genetic logic gates for robust digital-like synthetic biology[J]. Nature Communications: 2011, 2
[3] Hidde de Jong. Modeling and Simulation of Genetic Regulatory Systems: A Literature Review[J]. Journal of Computational Biology: 2002, 9(1): 67~103
 "
"