Team:TU Darmstadt/Modelling/Statistics
From 2013.igem.org
| Line 230: | Line 230: | ||
<br> | <br> | ||
<br> | <br> | ||
| + | |||
| + | <center> | ||
| + | |||
| + | <img alt="Test" src="/wiki/images/e/ea/DKL2.png" width="400" height="400"> | ||
| + | |||
<br> | <br> | ||
| + | |||
| + | <img alt="Test" src="/wiki/images/c/c4/Gender_Produkts.png" width="400" height="400"> | ||
| + | |||
| + | <br> | ||
| + | |||
| + | <img alt="Test" src="/wiki/images/7/79/XXGender.png" width="400" height="400"> | ||
| + | |||
| + | </center> | ||
| + | |||
| + | <br><br><br> | ||
<h2><font size="6" color="#F0F8FF" face="Arial regular">References</font></h2> | <h2><font size="6" color="#F0F8FF" face="Arial regular">References</font></h2> | ||
Revision as of 01:46, 5 October 2013
Information Theory
The DKL Analysis
In information theory the Kullback-Leibler-Divergence (DKL[1]) describes and quantifies the distance between
two distributions P and Q. Where P denotes an experimental distribution, it is compared with Q, a reference distribution. DKL is also known as ‘relative entropy’ as well as ‘mutual information’.
Although DKL is often used as a metric or distance measurement, it is not a true measurement because it is not symmetric.

Here, P(i) and Q(i) denote the densities of P and Q at a position i. In our study, we use the DKL to describe the distances of the survey datasets from the human practice project. Therefore, we have to calculate a histogram out of the different datasets. Here, it is important to perform a constant binsize. In this approach we assume that a hypothetical distribution Q is uniformly distributed. To achieve this, we grate an appropriate test data set with the random generator runif in R.
Results
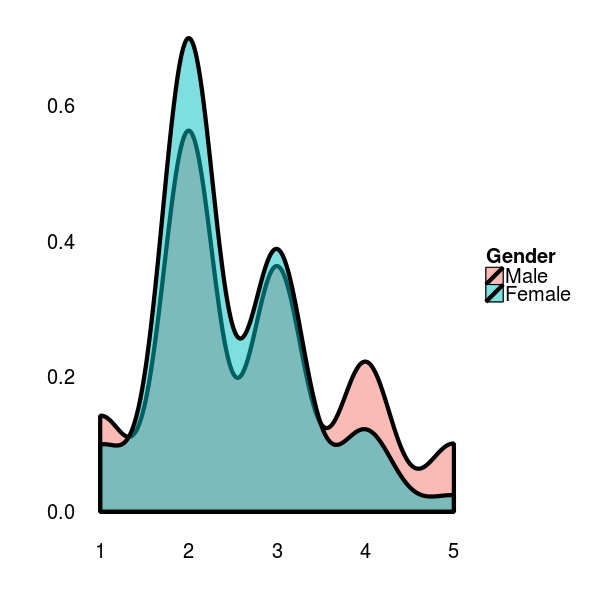

References
- Kullback, S.; Leibler, R.A. (1951) On Information and Sufficiency Annals of Mathematical Statistics 22 (1): 79–86. doi:10.1214/aoms/1177729694. MR 39968.
 "
"