Team:UT-Tokyo/Modeling
From 2013.igem.org
| Line 28: | Line 28: | ||
<p>For the reason stated above, we developed the model based on partial delay-differential equations with Hill functions that captured the activation and repression of protein synthesis, and Michaelis-Menten kinetics that captured enzyme catalysis. Finally we derived the following set of delay-differential equation model for concentrations of AiiA (A), TetR (T), LuxI (I), internal AHL (H<sub>i</sub>), and external AHL (H<sub>e</sub>)</p> | <p>For the reason stated above, we developed the model based on partial delay-differential equations with Hill functions that captured the activation and repression of protein synthesis, and Michaelis-Menten kinetics that captured enzyme catalysis. Finally we derived the following set of delay-differential equation model for concentrations of AiiA (A), TetR (T), LuxI (I), internal AHL (H<sub>i</sub>), and external AHL (H<sub>e</sub>)</p> | ||
| - | <img src="https://static.igem.org/mediawiki/2013/ | + | <img src="https://static.igem.org/mediawiki/2013/e/eb/Fig1.png" class="figure"> |
<p><b>Figure 1</b> delay-differential equations</p> | <p><b>Figure 1</b> delay-differential equations</p> | ||
Revision as of 08:24, 13 October 2013

MODELING
Our concept of Multicellular Analog Clock is based on qualitative assumption such as how negative feedback loop behaves, how AHL diffuses, and so on. To ascertain our system can function as an analogue clock, namely, to confirm the feasibility of our cell-cell communication included gene circuit, and to deepen understanding of behavior of the system, we conducted the following simulation.
DDE model derivation
Using DDE (delay-differential equation) analysis, we can conduct gene network simulation which accounts for delayed production of proteins. It is true that ODE (ordinary differential equation) analysis enables us to simulate rough behavior of complex gene networks, but if you want to simulate temporally more detailed behavior, ODE analysis is insufficient. Since when cells produce proteins including transcription factors, they must pass through processes of transcription, translation, maturation, transcription rate of genes reflects production of transcription factor after these processes' time delay. For this reason, we derived delay-differential equation in reference to [1].
For the reason stated above, we developed the model based on partial delay-differential equations with Hill functions that captured the activation and repression of protein synthesis, and Michaelis-Menten kinetics that captured enzyme catalysis. Finally we derived the following set of delay-differential equation model for concentrations of AiiA (A), TetR (T), LuxI (I), internal AHL (Hi), and external AHL (He)

Figure 1 delay-differential equations
We did not include an equation for LuxR assuming that it is constitutively produced at a constant level, which is adopted based on some references in which model development is performed on the same assumption ([1] and [2]). For model simplicity, concentrations of four proteins are approximated as having the same behavior. In equation (1), [Hi]τ and [T]τ mean corresponding proteins' concentrations before τ minutes. The parameters are described in the following.
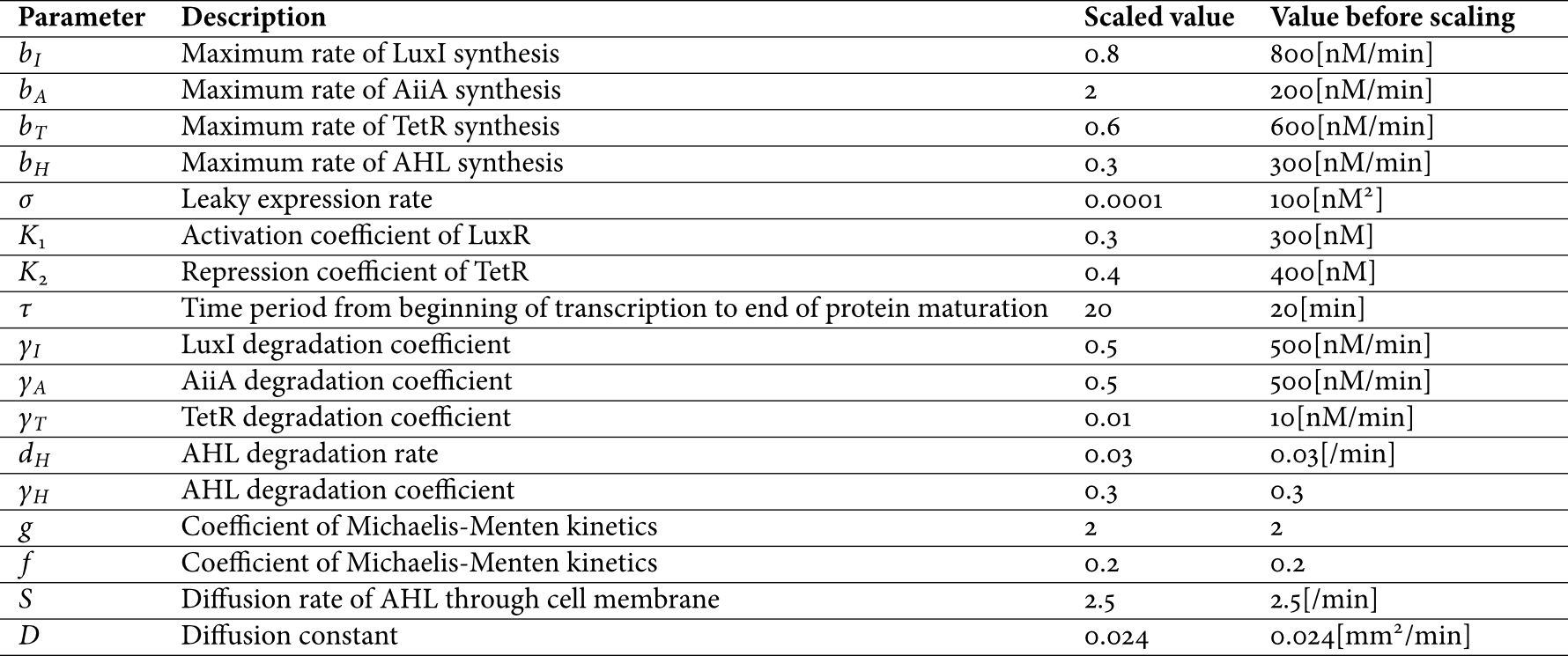
Figure 1 delay-differential equations
Result
You can get the result here!
Parameter sensitivity
To figure out the sensitive parameters in our system, we varied the parameters and investigated how the behavior was affected. This parameter sensitivity analysis let us know that LuxI degradation rate ( ) is sensitive, and the range of the parameter which realizes sustained moving of clock hand is limited. Therefore, it is thought that when our system doesn't experimentally function as we expect, we may improve it by varying this parameter in diverse ways.
[1]Danino, T., Mondragon-Palomino, O., Tsimring, L., & Hasty, J. (2010). A synchronized quorum of genetic clocks. Nature, 463(7279), 326-330.
[2]Tian, T., & Burrage, K. (2006). Stochastic models for regulatory networks of the genetic toggle switch. Proceedings of the National Academy of Sciences, 103(22), 8372-8377.
 "
"