Team:KU Leuven/Project/Oscillator/Modelling
From 2013.igem.org
Secret garden
Congratulations! You've found our secret garden! Follow the instructions below and win a great prize at the World jamboree!
- A video shows that two of our team members are having great fun at our favourite company. Do you know the name of the second member that appears in the video?
- For one of our models we had to do very extensive computations. To prevent our own computers from overheating and to keep the temperature in our iGEM room at a normal level, we used a supercomputer. Which centre maintains this supercomputer? (Dutch abbreviation)
- We organised a symposium with a debate, some seminars and 2 iGEM project presentations. An iGEM team came all the way from the Netherlands to present their project. What is the name of their city?
Now put all of these in this URL:https://2013.igem.org/Team:KU_Leuven/(firstname)(abbreviation)(city), (loose the brackets and put everything in lowercase) and follow the very last instruction to get your special jamboree prize!


Oscillator: Model
In this part of the wiki we will describe how we performed an analysis of our proposed oscillating system and the results. This text starts with a small introduction on what we want to achieve with this oscillator, a topic that is more thoroughly elaborated on the design page. Before we started the analysis that is stated here, we looked up how similar networks have been analyzed before in order to see what direction we will take. A full-scale analysis would go beyond the scope of the project so we will stick to an elaborate indicative study. The first step is to translate our network into ODE’s (ordinary differential equations), which we will make more realistic step by step. We will use these to see how easily sustained oscillations form. This is of course not the most impressive feature since there are many known networks that easily produce oscillations. We chose not to include the effect on amplitude and frequency, since that would make the scope of this study explode and the many assumptions we have to make, render it unrealistic. The important feature of our network is its synchronization features. In order to check whether our model achieves rapid resynchronization, we will solve systems of PDE’s (partial differential equations). Since those are a lot more computationally intense, we used the Flemish Super Computer Centre (VSC) in order to do our computations time-efficiently. The explanation of how the network functions and how it attains synchronized oscillations can be found on the page explaining the design. For the transformation into a biological network, we refer you to the wetlab page.
1.1 Exploring our possibilities
Firstly, it is important to clarify what we exactly mean with ‘parameter’. A biochemical system has a very high variability in ranges for transcription rates, translation rates, degradation rates, etc. On top of that these parameters are not perfectly quantified and are subject to changes in the conditions. We checked what part of the parameter space (Box 1) creates oscillations. There are possibilities for doing this in a purely mathematical manner. Tyson (2002) gives a good example of how to study systems that produce biochemical oscillations. Polynikis, Hogan and Bernardo (2009) described modelling approaches for gene regulatory networks more generally. This is typically done by investigating the eigenvalues of the Jacobian matrix of the system. This becomes increasingly more difficult when the number of parameters and variables increases. A high level of non-linearity complicates the study of the behaviour even further. In order to see what is possible we contacted Professor Dirk Roose, an expert in non-linear systems analysis. We explained him we want to investigate what parameter values create a synchronized oscillation. However, our parameter space consists of about 20 parameters that can each vary with more than a factor ten. On top of that we will have highly non-linear equations. Professor Roose told us this amount of variability would make a clean-cut mathematical examination of our model impossible . Since it is not possible to reduce our parameter space, without diverting from our goal of fully studying our system, we decided to use another strategy. We will study this enormous parameter space by generating random sets of parameters throughout this space. This offers a less theoretical, nonetheless effective means of assuring this model robustly produces oscillations.
Box1 | Parameter Space
We will explain this concept with a simple example. Let’s say we want an iGEM team (our system) to develop an oscillator. Two parameters of our system will determine whether this endeavour is successful. These parameters are the number of engineers in a team and the amount of coffee they consume per engineer. As to determine the parameter space we have to find relevant ranges for each of the parameters. We assume more than 10 engineers in the iGEM team is unlikely and a coffee consumption of more than 1.2 liter per day per engineer can also be discarded. The resulting parameter space for this two-parameter model can be easily visualised by a rectangle. This resulting parameter space can be probed and the parameter values we obtained were then used in a simulation which gave as an output whether an oscillator is produced or not. In the figure below we show the result of such a random probing of the parameter space. The blue dots represent unsuccessful endeavours and the orange dots successful ones.
 The results allow us to hypothesise on what is necessary to produce an oscillator. Apparently a higher amount of engineers still makes success possible, but only when the coffee consumption is not too high. We hypothesise here that this might be because the engineers get too much energy and start to fight amongst themselves.
We used a similar approach in the testing of our model, with some distinctions though. We deme parameter sets positive when synchronized oscillations take place. But we have 26 parameters and that makes it impossible to visualise our positive parameter space. So we chose another way to look at the parameter space and look at the total fraction of the parameter space that exhibits the wanted behaviour.
The results allow us to hypothesise on what is necessary to produce an oscillator. Apparently a higher amount of engineers still makes success possible, but only when the coffee consumption is not too high. We hypothesise here that this might be because the engineers get too much energy and start to fight amongst themselves.
We used a similar approach in the testing of our model, with some distinctions though. We deme parameter sets positive when synchronized oscillations take place. But we have 26 parameters and that makes it impossible to visualise our positive parameter space. So we chose another way to look at the parameter space and look at the total fraction of the parameter space that exhibits the wanted behaviour.
1.2 Derivation of the ordinary differential equations (ODE’s)
1.2.1 The preliminary system
The logical circuit of our oscillator is displayed in Figure 1 and for an elaborate explanation on this design we refer you to the design page. We will start with a preliminary translation of this network into a system of ODE’s, which is the most used method for modeling gene regulatory networks (Polynikis, Hogan and di Bernardo, 2009). An ODE cannot account for the fact that in reality each of the steps (like transcription and translation) take a finite amount of time. Danino et al. (2010) used delayed differential equations (DDE’s) as a solution for this problem but this complicates the mathematics enormously, especially when we want to take all our parameters into account. We will stick to ODE’s, since that should suffice for the study of our model. The extra delay should benefit the occurrence of oscillations because it helps diminishing peak overlap. The system of ODE’s is created by composing a rate equation for each of the six components of this preliminary circuit Figure 1. Those rate equations give the change of the components over time as a function of the amount of each of the components. The resulting system is displayed as Equation 1. Below we explain the meaning of the different components and afterwards we will explain each of the equations in this system. Further on we will derive the ODE systems for circuits that are slightly altered; by adding the fact that the production of quorum-sensing molecules goes through an enzymatic step and by using the implemented version of the OR gate.

The functions of the form 
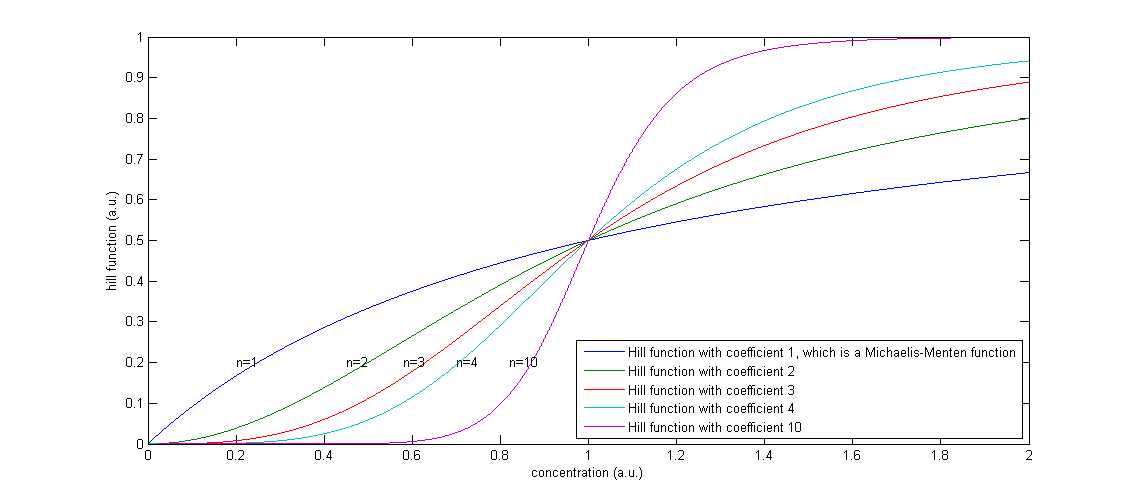 Figure 2: The effect of a higher Hill coefficient
Figure 2: The effect of a higher Hill coefficient
The other parameters in this model are the maximal production rates, which are indicated by β’s and the decay rates, which are indicated by α’s. The degradation term is proportional to the concentration of that component, in which the proportionality constant α can be seen as the percentage of the present proteins that degrades in one unit of time.
We will now discuss the different rate equations and how they are linked to the logical circuit of Figure 1. The concentration of each of the components changes because of a production and a degradation term. The production depends on the presence of the other components and the degradation is as described above. Specifically for A the production is activated in the presence of D and repressed in the presence of C. The logical AND gate can be seen as if both components have to give a positive signal (presence of D and absence of C) in order to have production of A. The format 


Figure 1: Logical circuit displaying our oscillator
1.2.2 Enzymatic production of quorum-sensing molecules
As mentioned on the design page the quorum-sensing molecules are produced by an enzymatic step. Equation 2 shows the equations that result in that behaviour. The transcription factors control the production of the enzymes rather than A and B directly. The production of A and B is modelled by using Michaelis-Menten kinetics (SA/(KA+SA)). To not overly complicate our model we will assume that the substrates SA and SB are at saturation levels. This means they are a lot higher than KA, KB respectively and the Michaelis-Menten consequently returns 1. This resulting system of equations is shown in Equation 3.

Equation 2: ODE system exhibiting the behaviour of the oscillator, including an enzymatic production step for the QS molecules

Equation 3: ODE system exhibiting the behaviour of the oscillator, including an enzymatic production step for the QS molecules with the assumption of saturation of those enzymes
1.2.3 Alternative OR gate
In the part before we used an actual OR gate, however, in the wetlab we use an approximation of a real OR gate. We implement the gene for production of C (D) twice, once with a promoter that is induced by A (B) and once with one that is induced by X (Y). This is easier to implement although the behaviour is somewhat different. There is now a higher expression when both the inducers are present. There is no difference in the fact that this displays a asymmetric time delay, of which the importance is discussed in the design page. This altered circuit is displayed as Figure 3.

Figure 3: Logical circuit displaying the our oscillator with enzymatic production of the QS molecules and the alternative OR gate
This is translated into Equation 4 by using the format 


Equation 4: ODE system exhibiting the behavior of the oscillator with enzymatic production of QS molecules at substrate saturation and the alternative OR gate
1.3 Matlab analysis
First we determined the ranges to which the parameters belong. This was done for the degradation rates (α), the production rates (β) and the thresholds (K). We chose random sets of parameters in these ranges and tested whether sustained oscillations take place. Because of the enormous parameter space we could not scan it entirely, but this method still proves whether the tested system inherently produces sustained oscillations. To conduct our computations we made use of the Flemish Super Computer Centre (VSC), which is a partnership of the five Flemish university associations. To use this we first had to rewrite the tests so they could be run in parallel on the supercomputer cluster at our university. Although this seemed straightforward, we encountered an obstacle in the generation of random numbers. When testing on the supercomputer, it appeared like we got 100 identical results in one test. The fault was rapidly determined: the way random number are generated in Matlab. By default, the seed Matlab uses to generate (pseudo)random numbers is always the same if this is the first command you execute. To solve this, we implemented a solution found on (http://www.walkingrandomly.com/?p=2755). This involved getting random numbers out of the Linux kernel random number generator and using these as a seed for the random number generator in Matlab. We tested several systems this way, starting with the simplest and building up to the final one. For each of these systems we checked how many of the tested sets of parameters produce oscillations. We used this to calculate the fraction of oscillating sets in the tested parameter space (see Box 1).
1.3.1 Selection of the parameter range
For the degradation rates of the proteins we assume they follow the N-end rule and are not in one of the unstable categories. This means the dilution rate controls the effective degradation rate and thus we use values that are appropriate for that. More information on how these values have been found can be found on the methyl salicylate modelling page. The ranges can be found in Table 1.
For the colony-wide molecules this approach for the degradation rate cannot be used, since they are present inside as well as outside of the cells. Those molecules thus become diluted when the volume of the colony increases, but not per se when the amount of cells increases as is the case for stable proteins. When we think about using quorum sensing molecules, the colony-wide molecules are metabolites. A potential problem might then be the slow degradation rate as encountered by Danino et al. (2010). On the wetlab page, we describe the use of an actively degrading enzyme as a solution for this issue of slow degradation. Since our model does not require a specific chemical species for oscillating, we will allow a broader spectrum of possibilities than through exactly that degrading enzyme. We will simplify the model by assuming a uniform degradation throughout the colony, but by allowing two decades of variance, we will still allow for a broad spectrum of possibilities. We will use the degradation (dilution) rate of the proteins as a mark for the degradation rate of the colony-wide molecules, since the volume of a colony also increases when the amount of cells augments. The two decades of variance in the degradation rate of colony-wide molecules will range from one tenth of the degradation rate used for proteins to ten times that degradation rate. Allowing values lower than the degradation rate used for proteins is based on the fact that the growth of the volume of a colony is slower than the growth of the number of cells. Allowing values higher than the degradation rate used for proteins is based on the possibility that the colony-wide molecules are for instance actively degraded by some produced enzymes or a fast spontaneous degradation. These values can also be seen in Table 1.
Box2 | Steady-state concentrations
A steady-state concentration of proteins can be easily determined by setting each of the rates to zero. In the case of maximal production rate, the rate equation has the following form: 



In the case of metabolites, that are produced by enzymes the rate at full production capacity equals 


The maximal production rates (β) of the proteins can vary enormously, for instance due to differences in copy number. However, the goal of this oscillator is to have the components in the chromosomal DNA of the cells. We thus assume values that are in the rage of production rates of chromosomal genes. For those ranges we use the assumption that the steady-state concentrations of proteins is equal to β/α (see Box 2), we used the α’s as determined above and we use protein abundances as determined by Ishihama et al. (2008). They determined a steady-state concentration for enzymes to be around 65 per cell and for components of the biosynthetic machinery to be around 105. An important remark is that the assumption that steady-state concentrations are equal to β/α is only correct for as long as the production is fully on and not when there were some inhibitory effects active. This means that the lowest protein abundances that are determined by Ishihama et al. can be a lot lower than β/α due to for instance regulation of the production rate, which was consequently not at its maximum. When the production rate is only half of its maximum for instance, the steady-state concentration of the protein is only equal to 0.5∙β/α instead of β/α, which means the lowest values determined by Ishihama et al. be too low. On the other hand the highest values might also be too high, since we are not dealing with components of the biosynthetic machinery. It thus seems wiser to us to discard the extremes and only probe between 6.5∙10^2 and 10^4. We will use these values and transform them to production rates by using the formula from Box 2 and the degradation rates from Table 1. The calculated values can be found in Table 1.
The maximum production rates due to the enzymes cannot be determined this way, but also span an enormous range. Shaefer et al. (1996) found proof, however, that enzymes that produce quorum-sensing molecules have a low maximum production rate, and they found specifically for the Vibrio fischeri LuxI protein that β equals 1.1 molecule per minute. Since our model is not confined to one enzyme, we will again test a bigger scope. We will again use a range of two decades for this parameter, as can be seen in Table 1.
The final parameters we will look into is the threshold value. Our method will consist of randomly picking production rates degradation rates of metabolites. As mentioned in Box 2 the steady-state concentration at full production capacity equals β/α for proteins and 

Table 1: Parameter ranges
1.3.2 Setup of the in silico experiments
We have already skimmed the fact that we will use random probing of the parameter space in order to establish the fact that sustained oscillations take place. Here we will discuss how we exactly probed the parameter space, what we took as initial conditions for the ODE solver and how we tested for oscillating behaviour.
Since we cannot assume any probability distribution, we will stick to a uniform distribution for each of the parameters. Each of the parameters will be allowed to vary independently from one another, except for the protein degradation rates and the metabolite degradation rates. Those will all be chosen to be the same since the value is based on the growth rate of the colony, which is of course the same from the perspective of different proteins within that same colony.
The initial conditions determine quite a lot of the behaviour of the network when there are non-linear functions involved. In order to test whether the system behaves as predicted we will use initial conditions that correspond to the explanation on the design page. This means we start with a high concentration of A and zero of each of the others. It is now only necessary to determine what qualifies as a high enough concentration. For this we use the maximum of KAX and KAC as a point of reference because that can be seen as the threshold for A to have an impact. We will simply chose twice that threshold, which should suffice to spark the system.
Detection of oscillating behaviour was done differently for tests involving ODEs and PDEs. The latter had to be checked manually, because of their often very different appearance. The ODE tests however were checked on stable oscillations by a self-written script. This program takes the Fourier transform of the signal after the transient part using the Matlab command for Fast Fourier Transform (FFT). The the components of this FFT are split into the zero frequency component and all other components. Then, the sum of the absolute values of the components with a nonzero frequency is compared to the absolute value of the zero frequency component. If this ratio is greater than one, the signal is marked as oscillating. Practically, this means that the signal has to have some periodic components that are of the same order of magnitude as the zero frequency component, which is the average of the signal. Signals with negative values were automatically discarded due to their physical impossibility. If any of the signals in a test run was oscillating, the whole test run was marked as positive.
As an output we will determine what the oscillating fraction of the tested parameter space is. This is a good measure to find out how easily the system reaches oscillations. Since we randomly probe throughout the parameter space and find a binary result of either oscillating or either not. Since this is a Bernoulli trial process, we can calculate the 95% confidence interval of the fraction of the parameter space that oscillates. The formula displayed as Equation 5 gives that 95% confidence interval and according to Brown Cai and DasGupta (2001) this formula should function well as long as both n∙p > 5 and n∙(1-p) > 5. This means that only in the case of a fraction close to 0 or close to 1 there can be a problem. However, when it is that close to either of the extreme values, the results are already clear enough because it simply means the system hardly ever oscillates, or oscillates almost all the time. When p^ is as close to 1 that n∙p > 5, that maximum 4 out of 100 tests produced a non-oscillatory system and we can definitely say that the system easily produces oscillations in that parameter space.

Equation 5: 95% confidence interval for the proportion of success in a Bernoulli trial process.
1.3.3 Testing the preliminary model
A first test using the preliminary model, which is shown in Equation 1, did not frequently give oscillations. This is easily explained because of the fact that the thresholds, who were chosen of the same order of magnitude as the theoretical maximum, were never approached. The reason the levels of the components do not reach that high level is because of the many direct and indirect inhibitory effects within the system. Those inhibitory interactions keep the production rates, and thus the concentrations, well below their theoretical maximum. Since the thresholds are far from reached, this also means there is no activation of subsequent components and thus the whole process of oscillating does not get sparked. As a control for this hypothesis we tested how the oscillating fraction of randomly picked parameter sets varies when different ranges for thresholds are used. We did this by taking only a fraction of β/α as the upper bound and again a lower bound that is one tenth of the upper bound. This has been done each time for a small pool of only 100 randomly chosen sets of parameters and the results are shown in Table 2. From an upper bound of 0.05∙β/α onwards oscillations are far from rare and further lowering of the thresholds does not change that feature.

Table 2: Effect of threshold height
We will thus use a slightly altered parameter space and continuously test several of them. We will let the thresholds vary from 0.01∙β/α to 0.1∙β/α, 0.001∙β/α to 0.01∙β/α and 0.0001∙β/α to 0.001∙β/α in three different tests. This also changes the thresholds for metabolites accordingly and these new parameter spaces are displayed in Table 3.

Table 3: Revision of the parameter space
The different resulting behaviours for the situation in which the protein thresholds are allowed to vary from β/α∙10-3 to β/α∙10
Figure 4 a to d shows the prevailing behavior, which are oscillations in which C reaches a lot higher levels than A or X. Figure 4 a shows a typical example of such oscillations and in Figure 4 b this has been zoomed in on A and X. Figure 4 c and d show another interesting example of oscillations, in which C is of the same order of magnitude as the others. This only happens a few times, which is probably due to the fact that C has two means of activation, but none of inhibition. This makes the production of C more intense and last longer. The specific equations we used probably also have a big effect on this, as well as the chosen parameter ranges. Another remark that can be made is that the levels of A and B are also low in absolute terms. Strictly speaking, this is not bad, since we made a lot of assumptions which mean quantitative features like the amplitude and frequency are unreliable. As mentioned before we only want to assert the qualitative features of this model like oscillations and synchronization. We can now already see that in this simple case oscillations do occur and after the discussion of Figure 4 we will give a confidence interval of the fraction of the parameter space in which oscillations occur.
The occurrence of oscillations like the one displayed in Figure 4 c and d are not qualitatively different from those from Figure 4 a and b. Though they allow for a better description of how the several components relate to one another. It shows that the production of C goes on for an extended period even after the disappearance of A, which is the effect of the coherent type 1 feed forward loop. This feature can be easily related to the presence of X even after A has disappeared.
The other type of behaviour this model showed was reaching a steady state. An example of this is shown in Figure 4 e. In this image the system starts with oscillations in C that are damped, but it can also be that the steady-state is reached without ever oscillating. This is of course unwanted behaviour, but regardless of the parameter set used, there are always initial conditions that make the system reach a steady-state. In a heavily non-linear system of equations like ours, there are always some of those steady-states that are stable.
Theoretically there are two other types of behaviours possible in the case of continuous non-linear equations. The first possibility is extinction, which is a steady-state situation in which all of the components their levels become and remain zero. This behaviour has only been observed when using thresholds that are way too high. The second other possibility is an explosion of the system. Then one or more of the components’ level rises indefinitely. This type of behaviour is not possible in the systems we will study, since each component has a degradation term that is proportional to the level of that component and the production term is not and has a maximum value.
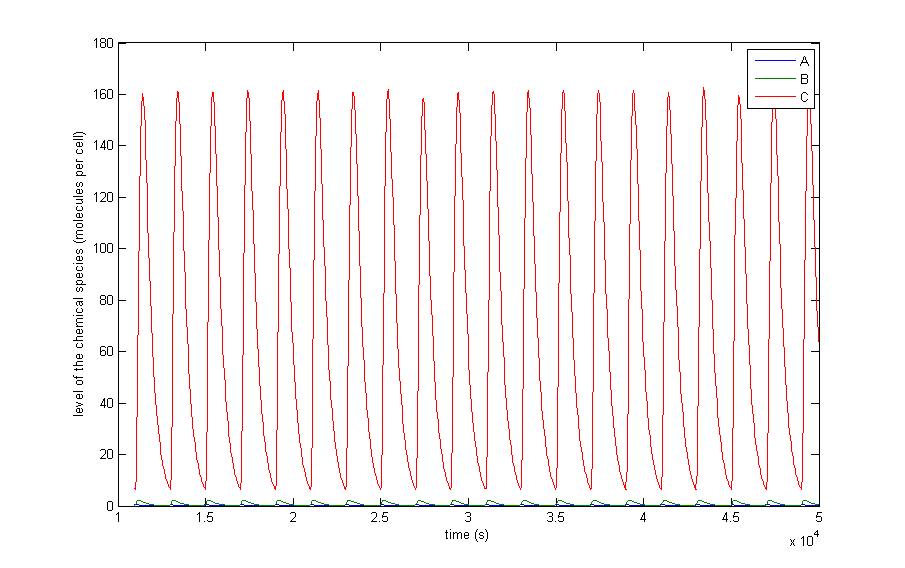


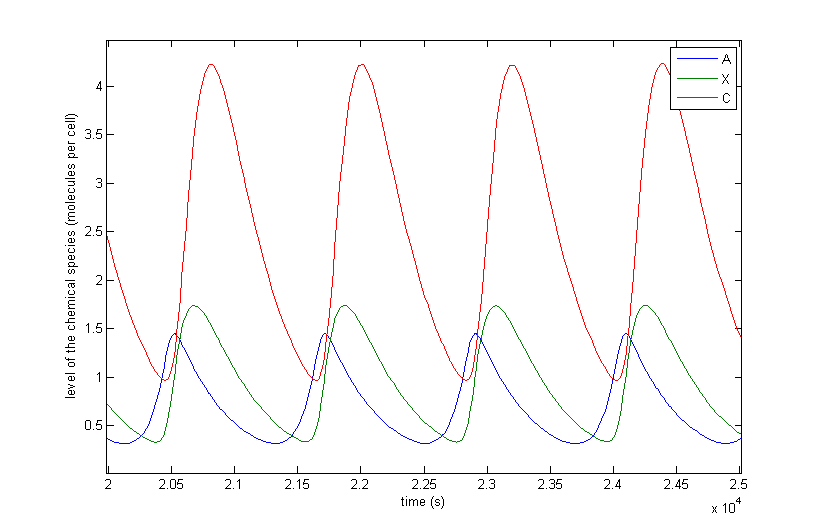

Figure 4: The resulting behaviour| a, the typical oscillations, b, the same as a but zoomed in at A and X, c, oscillations in which the difference between A and X on the one hand and C on the other are not so different, d, the same as c but zoomed in at 4 periods, e, an acquired steady-state, f, a steady-state in which each component returns zero.
We then sought the fraction of parameter sets that result in oscillations for each of the three situations. The resulting confidence intervals for that fraction can be found in Table 4. None of the confidence intervals overlap each other, so lower threshold ranges significantly increase the fraction of oscillations, which supports our explanation that oscillations could not occur due to the fact that the thresholds could not be reached. The oscillating fraction is high, showing that this system of equations inherently produces oscillations.
 Retrieved from "http://2013.igem.org/Team:KU_Leuven/Project/Oscillator/Modelling"
Retrieved from "http://2013.igem.org/Team:KU_Leuven/Project/Oscillator/Modelling" "
"




