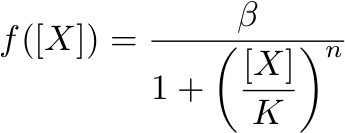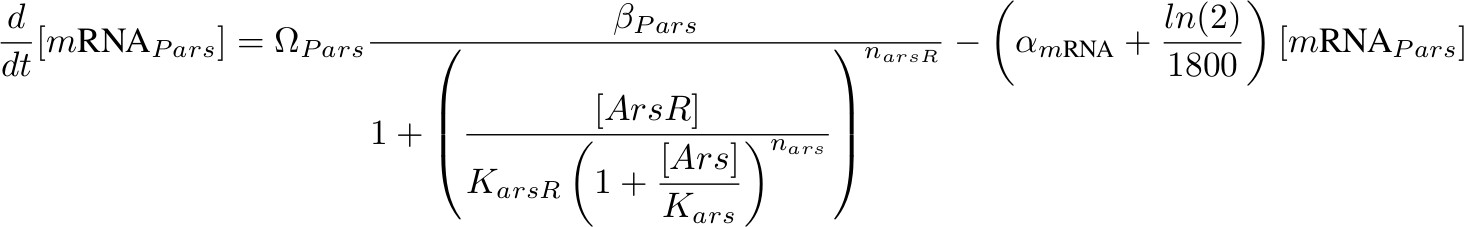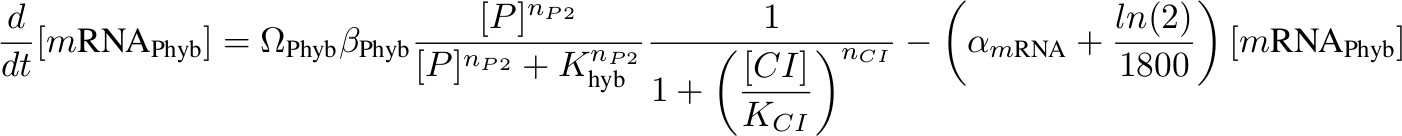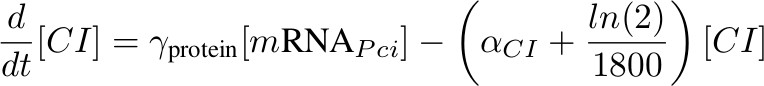Deterministic Model

Introduction

Our objective was to assemble a system that could respond to different concentrations of a specific contaminant in water. More specifically, the idea was to produce different amounts of a colored pigment depending on the concentration of the contaminant present in water.

We worked with Arsenic knowing that an arsenic detoxification operon (Ars operon) exist in nature and more important, it exists as a biobricks.

To skip directly to our mathematical model click here.

Got Ideas?

For our biosensor we came up with three different designs each one motivated on improving the flaws detected while analyzing the previous ones using mathematical models as our main tools. We describe briefly the first two designs, which were rejected, to emphasize the importance of mathematical model to gain insight on how our system works and as a feasibility study taking into considerations .

Arsenic promoter + ArsR + Reporter

First we tried to keep it as simple as we could. Figure 1 shows our first design which, in theory, produces different responses to different concentrations of arsenic in water. Figure 2 shows a simulation graphing the time series response of the Pars promoter-arsR for different concentrations of ars.

Figure 1: Our first biological design: Arsenic promoter repressed by ArsR wich is inhibit by Arsenic.

Although we have a system that recognize and respond differently to different concentrations of arsenic since our reporter was meant to be a colored pigment (the reasons for this are detailed in the project tab) scale tuning needs to be taken into account.The reporter is downstream the Pars promoter and the design shows little flexibility, i.e. few available parameters, to produce a discernible colored output.

Another problem is that we aimed to use a reporter (unknown at that time) with a low degradation rate thus if the production of the pigment didn't stop at some point, accumulation of the pigment leading to eye saturation would become a problem. Although the model shows a steady state (figure 2) this accounts only for one bacteria with the degradation/dilution rate governed mainly by dilution.

Nothing else to do but to come up with a different idea for our design. Note that the model of the Pars promoter + ArsR is still useful because is the main block of any design to detect Arsenic in water. For details on how we model this click here.

Toggle Switch + Quorum Sensing + Reporter

Figure 3: Graph of the nullclines of a toggle network with (a) bistability consequence of repressor cooperativity and (b) monostability consequence of no repressor cooperativity.

Our second design was based on the work done by the Grenoble Team 2010. They coupled a toggle switch with a quorum sensing circuit to produce a system that produces a colored pigment if and only if a specific IPTG/Hg concentration ratio existed in the water. IPTG concentrations are determined previously so as to activate the system at a desired Hg concentration.

Two main problems (among others) arised from the mathematical analysis of this system:

• The minimum requirements to obtain bistability is that at least one of the inhibitors must show cooperativity greater than one. Still, bistability will rely on the strength of the promoters.The lack of robustness of the system based on its dependence on cooperativity and promoter strength made the idea of having a modular device capable of working with a set of promoters-inhibitor impossible to achieve.

• The initial setting makes the toggle harder to switch back and although the Grenoble Team proposed a possible solution they never effectively tested it. This attempted against our desire of making a functional device and not a theoretical device.

Temporal control of reporter expression with an Incoherent-FFL

Parallel to the Toggle Switch + Quorum Sensing design we came up with an idea that could solve the problems of our first design: Pars + ArsR + Reporter.

We wanted a system that could:

1. respond differently to different concentrations of a specific contaminant.
2. stop in time to avoid the accumulation of our reporter. Keep in mind that our reporter was meant to be a coloured pigment with low degradation rate so you could see the response of the system with your naked eyes. We wished to avoid eye saturation of the pigment.

We knew that Pars + ArsR could satisfy our first requirement but we needed a kind of "timer" to meet our second requierment plus some sort of amplification system to calibrate the Arsenic promoter sensibility range with the "naked eye sensibility".

Based on [http://www.pnas.org/content/101/17/6355.long Basu 2004] biological network, we designed our own which met our basic requirements. For a detailed description click here.

Mathematical Model

The more you know =★: Before starting to talk about our model, if you know nothing about mathematical models of gene networks we highly recommend Uri Alon's book: An Introduction to Systems Biology.

Introduction

With our model, we wanted to understand qualitatively the general behavior of our system and its feasibility. In theory, we knew what to expect from the system but when simulated, unexpected behaviors may arise.

Figure 4: Scheme of our simplified gene network.

Figure 4 shows a simplified version of our biological design consisting of an amplifying system + Incoherent feed forward loop (IFF) of three steps. In our actual biological design we had a four step IFF. A middle step would only add a lag time for repression to occur. No significant change on the general behavior was observed if ignored so we took one step out to keep the circuit as simple as possible in order to gain insight. Click here to see the missing step. In case you notice, we wrote CI instead of C22 because the latter is from the family of lambda CI and in terms of parameters we assume they are the same.

The use of ordinary differential equations to model the system is a normal approach when studying gene expression. The input functions used to describe gene expression are detailed in the next section.

Input functions for gene expression

To describe the transcription rate of a gene under the influence of a transcription factor we use the family of gene input functions known as Hill functions:

Hill function for activator

Hill function for repressor

Hill function for repressor lifted by inducer

where β is the maximal expression level of the promoter, [X] is the concentration of protein X and K the activation coefficient. It defines the amount of X needed to significantly activate or repressed a promoter. [I] is the concentration of the molecule that inhibits the repressor [X] where K_I defines the amount of [I] needed to significantly inhibit [X].

Equations for mRNA Transciption

Our system consists of four promoters, thus we need to model four different types of mRNA, each one with different transcription rates depending on the promoter strength. Each type of mRNA was labeled using the names shown next to the promoter in figure 4. By identifying one promoter with one mRNA we are assuming no difference in mRNA concentrations for different genes under the same promoter. This assumption is not too risky considering the lengths of our constructions.

Each equation describing the rate of transcription includes a production term according to Hill functions competing against a degradation (α) and a dilution term. The dilution term was calculated considering one cell division every 30 minutes. Ω accounts for the number of plasmids.

[mRNA P_ars] – repressed by ArsR which is inhibit by Arsenic

[mRNA P_luxR] – constitutive promoter

[mRNA P_CI] – activated by P complex

[mRNA P_hyb] – activated by P complex, repressed by lambda CI

we assume no competition between activation and repression because the binding sites of complex P and lambda CI are not physically entangled.

Equations for Protein Translation

Protein rate of translation is proportional to the correspondent mRNA concentration which competes against the degradation + dilution term. The dilution term was calculated considering one cell division every 30 minutes.

• γ is the translation coefficient and is the same for all proteins.

• P is a complex of HSL and LuxR. Its degradation rate is the same as the one for LuxR because the latter has a faster degradation rate than HSL. Upon P degradation, HSL protein remains.

• K_P and K_-P are the association and dissociation coefficients respectively of HSL and LuxR to form complex P.

• HSL diffuse through the cell membrane at a rate θ.

• μ is the coefficient of enzymatic production of HSL.

[ArsR] - repress P_ars

[luxI] - triggers HSL production

[luxR] - forms complex protein P with HSL

[HSL] - forms complex protein P with luxR

[P] - complex protein HSL + luxR. Activates P_CI and P_hyb

[CI] - inhibits P_hyb

[RFP] - colored pigment

Results

Figure 5: Simulation graphing the time series response of the system with Arsenic added at t=0.

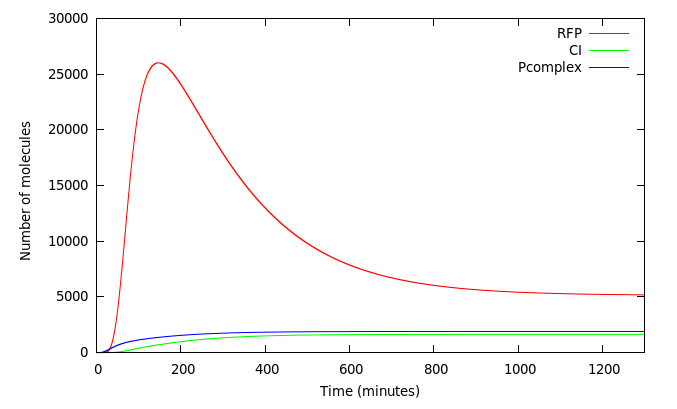
We wanted to analyze how our design worked. Figure 5 shows the system activated at t=0 by a 40000 molecules of Arsenic. The red line shows the concentration of RFP in molecules. As expected, complex P activates P_rfp and P_CI simultaneously and its not until CI accumulates that it represses the expression of RFP 200 minutes from the initial kick.

Figure 6 shows [mRNA P_ars] and [mRNA P_rfp] induced in the presence of different concentrations of Arsenic as detailed in the graph. The pulse of [mRNA P_ars] at t < 50 is in fact a damepd oscillation product of the smooth Hill function that represents the repression of ArsR. [mRNA P_rfp] presents a behavior as predicted by Basu 2004 with almost the same biological system but without modeling the effect of Arsenic as inhibitor. They made simulations at different rates of HSL increase (the same condition we have with different Arsenic concentrations) and obtain that for higher HSL rates of increase they obtained shorter and bigger pulses but when the HSL increase rate is lower, the initial buildup of both RFP and CI is correspondingly lower leading to pulses with longer delays and with less amplitude.

Figure 6: Simulation graphing the time series response of mRNA of the system with different concentrations of Arsenic all of them added at t=0.

Once we fully understood how our system worked, we analyzed what happened if Arsenic activated the system at t > 0. Figure 7 shows the results of the simulation.

Because of lack of ArsR at t = 0 promoter P_ars starts expressing mRNA P_ars triggering the IFF loop. Arsenic is added at t = 350 min as a step function, forcing the IFF to reactivate. You can clearly see the effect of Arsenic by observing [RFP] in Fig. 7 (b).

Figure 8 shows the system responding to different concentrations of Arsenic added at t = 350.There is an appreciable difference in [RFP] and different final states in each case.

Figure 7: Simulation graphing the time series response of (a) mRNA and (b) protein expression of the system with only one concentration of Arsenic added at t=350 min.

Figure 8: Simulation graphing the time series response of RFP protein expression with different concentrations of Arsenic all of them added at t=350 min.

Conclusions

Our third design works as expected generating a different response under different concentrations of Arsenic. If Arsenic is added at t > 0 the difference between the outputs for different concentrations of Arsenic may diminished. We can explore an alternative to mantain the system shuttered until the water and Arsenic is added. Problems may arise because of HSL+luxR saturation.