Team:Dundee/Project/MathTheory
From 2013.igem.org
Insight to the Mathematical World
Aims:
Using mathematical tools to allow us to predict the limiting factors in the production of PP1 and its mopping applications. Working alongside the biologists to produce models which are relevant and can predict what is expected to happen during the synthetic engineering of the mop and detection bacteria.
Detection Comparison:
The current method for detecting toxic levels of microcystin is to take a sample of water from different regions of the site being investigated and then to carry out high performance liquid chromatography (HPLC). This process currently takes approximately 24 hours, we hope to reduce this to a more suitable 1 hour.
Assuming the cyanobacteria undergo binary fission and grow unbounded we were able to determine how the problem increases over 24 hours in comparison to 1 hour detection. where MC(t) is the number of microcystin at time t b0 is the initial number of algae
The ratio for time t=24:1 is 8.4million:1. To put this into perspective this is the same as the height of the empire state building compared with the length of 7 E.coli bacterium. This model therefore emphasises that the 1 hour detection period is much more efficient and worth pursuing.
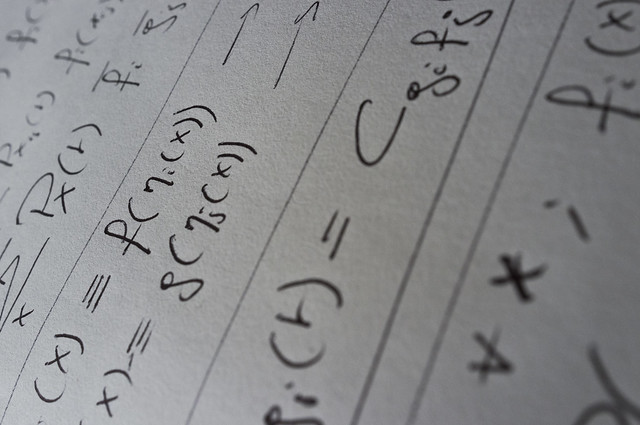
Geometric Packing:
We considered different limiting factors of our mop bacteria. The factor discussed in this section is the maximum number of PP1 which can fit either on the surface of B.subtilis, or in the periplasm of E.coli. We considered the volumes of the bacteria and PP1 and used a cube approximation that took into account volume which was wasted, in packing, by the spherical shape of the protein. For this model we assumed there were no other surface proteins and protein production was not limited by any factors.
Calculations show the maximum number of PP1 which can fit on the surface of B.subtilis is between 60 000 -70 000. From the average we can calculate that the number of bacterial mops required to clean a toxic level of microcystin in a litre of water is 1.40x1010.
In E.coli, PP1 which would bind microcystin is free-flowing in the periplasm. The volume of the periplasm is much greater than the surface of B.subtilis. Therefore E.coli has the capacitive potential to be a more efficient mop. The maximum number of PP1 which can be packed into the periplasm is between 150 000 -200 000. Consequently, less bacterial mops are required to clean the same level of microcystin: 0.52x1010.
When we have accurate numbers from the biology team on how many PP1 are attached to the surface or in the periplasm for B.subtilis and E.coli respectively, we can compare these numbers and compute the efficiency of our PP1 expressing bacteria.
Transcription, Translation
An Ordinary Differential Equation (ODE) uses a function f(t) to describe how the output changes as a result of changing the input dx(t)/dt. For example how PP1 concentration changes with time in a single cell. In order to model transcription and translation of PP1 we used a system of ODEs , which is more than one ODE where the outputs are coupled.
We used law of mass action to obtain a system of ODEs to describe the production of mRNA to PP1. mRNA and PP1 are coupled in the sense we need mRNA before we can produce any PP1. Also, the mRNA is not used up. We also took into consideration the degradation rates of mRNA and PP1 which are denoted as .
- k1 – rate mRNA production - 4.98x10-9
- kd1 – rate mRNA degradation – 1x10-2
- k2 – rate PP1 production – 4x10-2
- kd2 – rate PP1 degradation – 4x10-4
Figure 1. How mRNA and PP1 are produced over 20 minute cell division time. Note scaling on PP1 compared to mRNA.
Figure 2. A steady state is when the quantities describing a system are independent of time – they reach an equilibrium i.e dx/dt = 0. The steady state for (mRNA, PP1) is (0.04, 0.04) corresponding to a non-dimensionalised system. This plot demonstrates that during a 20 minute cell division period mRNA reaches the steady state but PP1 does not.
Figure 3. This plot shows that given a time longer than cell division time both the mRNA and PP1 eventually reach their steady states.
 "
"
