Team:SUSTC-Shenzhen-A/Modeling
From 2013.igem.org
Game theory
Stategy for the Classic Prisoners' Dilemma.
Abstract
Our model is to simulate an E coli cell-cell mutual help system that we are implementing to study the class game theory problem of prisoner's dilemma. Speciafically we designed two types of E coli cells to act as the two “prisoners” in a single enclosed environment with toxic chemical . The behavior of each “prisoner” under isolated interrogation is designed with constitutive promoter of different strength, with the weaker promoter mimic defect and the stronger promoter mimics cooperates. The results of such promoter is to detox the other cell while poison itself. The fate of one “prisoner” is related to the growth rate or density of one particular cell. We used mathematic modeling to quantitatively explore the consequence of each strategy of the classic prisoner’s dilemma.
So, how do we emulate this prisoner’s dilemma using genetically engineered E coli?
The toxic chemical is antibiotics Zeocin, which can be detox with the expression an antidote gene (zeo-resistent gene) to neutralized Zeocin. Without the antidote, the cell will either grow slower or die, with the antidote, it would grow happily. If “prisoner A” is collaborative to “prisoner B’, it would have a strong promoter to express an enzyme LasI to produce 12-carbon AHL (3OC12-HSL), a quorum sensing molecule to help B’s survive and grow in the environment. In the mean time, A itself makes sacrifice by also express an toxic protein that only worked on itself. The beneficial cell B utilizes the 3OC12-HSL to turn on an antidote gene (zeo-resistent gene) to protect the cell from the toxic chemical. If A cell is the traitor, it would not produce 3OC12-HSL that could help B cell, and in the meantime prevent production of toxic protein to itself. We use tetA, a tetracycline transporter which could also transport toxic Nickel ion into cell as the toxic protein. The B cell has the same design except that it expresses enzyme LusI to produce a different AHL (3OC6-HSL) and senses the 3OC12-HSL. The A cell can sense 3OC6-HSL and produce the antidote to zeo. The cell with more antidote protein and/or less toxic protein will grow faster, which in our system suffer less “jail time”.
The reason to use mathematic modeling
As a whole system, it is the mutual interest for both to cooperate. However if one chooses to cooperate, it may risk that other would enjoy its collaboration but defect it. It’s a complex problem that how our prisoners choose their strategies to ensure their survival. We would like to explore various strategies and the consequences using mathematic models so as to explain experimental data. We also want to find interesting alternative phenomena that do not exist in the classic prisoner’s dilemma.
the model
We model the density dynamics of the two cells over time based on the degree of their collaboration. Our model is consistent of ordinary differential equations for the densities of two cell types and two AHLs. The detailed description of all the equations and parameters are described here

What's the difference?
Our E coli system does not entirely mimic the classic prisoner’s dilemma. Since a cell population can grow or die off, the AHL it produces could also vary independend of its cooperative spirit. There are some interesting alternative scenario.
So our prisoner have a chance to make a dynamic choice, they can decide to what level the collaboration will be put into effect. The degree of collaboration is also directly related to the well being of the cell, namely its concentration. This adds another level of collaboration without the cells themselves realized it. This important difference makes our system more close to the realistic.
The prisoners will never really die in a classic situation, but in ours there exist some possibility that one type of cell can actually die out which will result in a big crash of the entire population. This is what we should key our eyes on.
Numerical experiments
To confirm whether our simulations can work out a good result, we want test some important parameters to see whether our subsystem can work properly,
1.1.Solitary confinement with toxic Zeocin
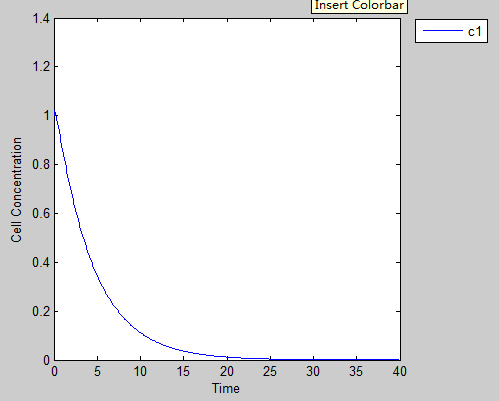
We put our prisoner in a solitary confinement to see what will happen to this poor man. This will help us understand how powerful the punishment is as well as tell us how much Zeocin we should use to create a temperate environment stress. As we can see from this figure, the antibiotic leads to a quick death of our prisoner. Without help the prisoner can hardly get out of it fate.
2.2. Solitary confinement with environmental AHL to help neutralize detox Zeocin
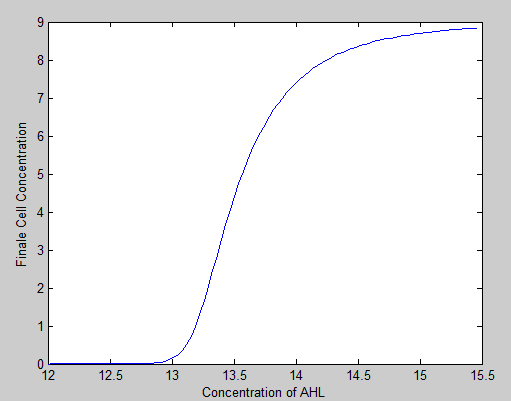
Environmental AHL could detox the cell from Zeocin by inducing the production of Zeo-R protein. The relationship between the AHL concentration and cell growth in solitary represents the key measurement of cell-cell collaboration. In order to quantify it, we vary the 3OC12-HSL concentrations , and simulated the final B cell concentrations. Alternatively we vary the 3OC6-HSL concentrations , and simulated the final A cell concentrations. In either case, there is only one cell type to isolate the effects. These results tell us some critical elements of the system such as whether there exists any sensitivity difference of AHL between the two cells. It could provide us with better understading of the cooporativity between these two cells. For instance, as shown in the figure below, there is a steep curve indicating the sensitivity to the AHL concentration at around 12.8. Once AHL goes above 12.8, the growth constrains caused by Zeocin is quickly neutralized. Such nonlinear response curve provide almost switch-like sensitivity to the density of the other cell type in the mixed population, which should provide very different behavioir with shallow relations such as linear.
3.3.The classic prisoner’s dilemma
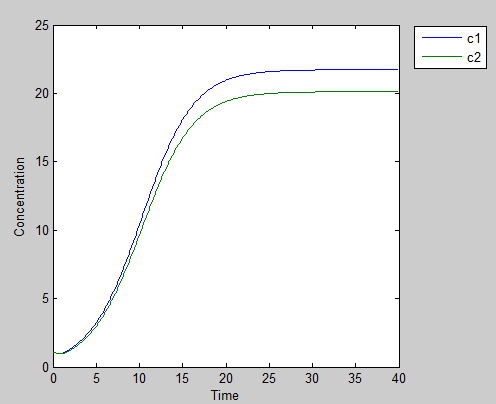
Scenario 1: Cooperativity: mutual benefit
If both of our prisoners help the others by producing AHLs, in the end both will grow to high cell density even though they sacrifice them self by expressing tetA and bring in toxic Nickel. This produce the best outcome for both cells.
Scenario 2: One traitor: punish the good guy
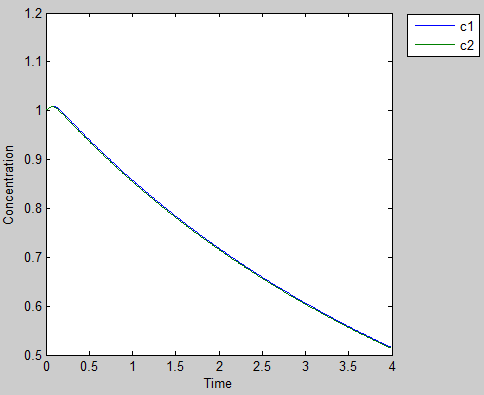
If one of our prisoners decides to defect the other guy and still get help from the other,he may be well benefited at first
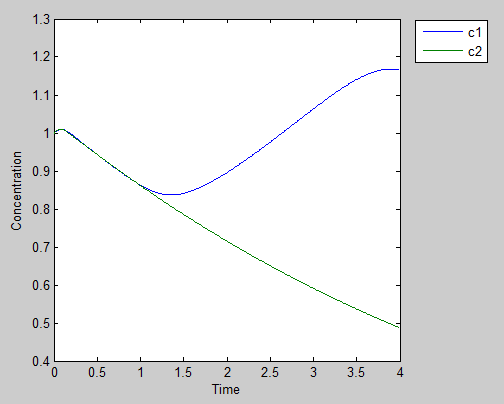
However, with the cooperator gradually dies off, the amount of AHL it produces decreases. While each cell are still in the spirit of helping the defectors, the dwindling population results in effective defects and cause the fast growth defector to lost Zeo-R protein and succumb to Zeocin, which leads to lost of both populations. This scenario is likely more realistic and happened in real life such as ecology and politics.
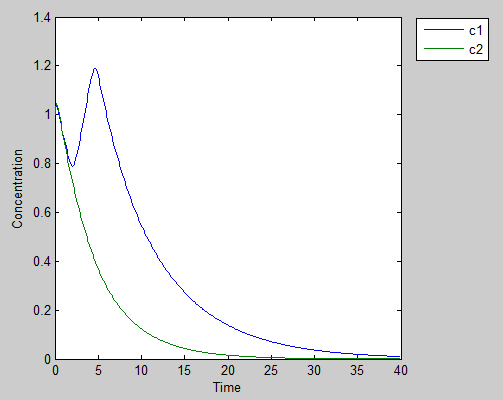
Scenario 3: no bad deed goes unpunished
If the both guy wants to take the advantage of the other guy’s sacrifice without giving back, they will end up receive harsh penalty and die off, although it is slower than the poor guy in scenario 2.
Oscillation and crush
The above scenarios assume both the prisoners have an identical physiological and psychological characters, meaning all the functions and parameters except for the defects/cooperates decision. According to this assumption, every cell can act the same behavior when meet the same change in the environment. However in reality, two pieces of leaves will never coincide in the world, and two prisoners could have different personalities. In our system two type of cells use different quorum sensing system should have different parameters. What will happen if we put two people with different sensibility of other’s goodwill into this dilemma? To achieve this we simply adjust the Hill coefficient of the differential equation of Zeo-R. What we found is in the figure below.
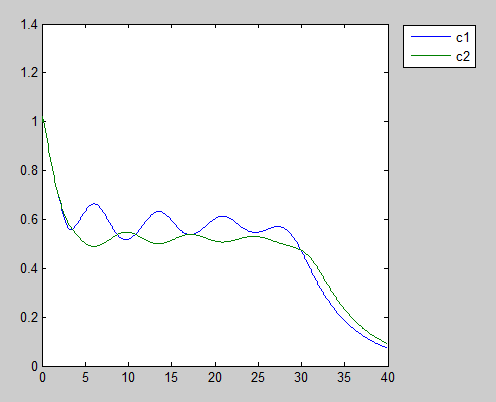
There is appears a clear tug-of-war game between our prisoners. The oscillation gradually damped. Usually a damped oscillation leads to a stable equilibrium. To our surprise this oscillation results in crush at certain unpredictable time. Perhaps it could be used to explain realistic game theory scenario in action.
This media liked the whole modeling of our project.
Media:modelingsustc.pdf "
"