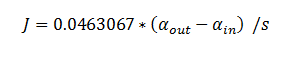Team:SydneyUni Australia/Modelling Results

From 2013.igem.org

(Difference between revisions)

Revision as of 03:20, 28 September 2013

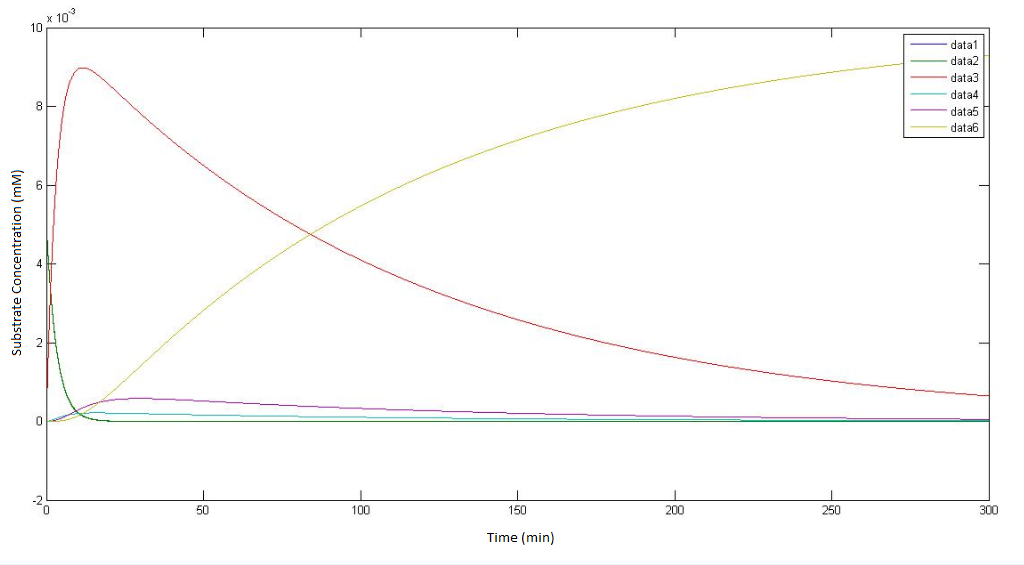
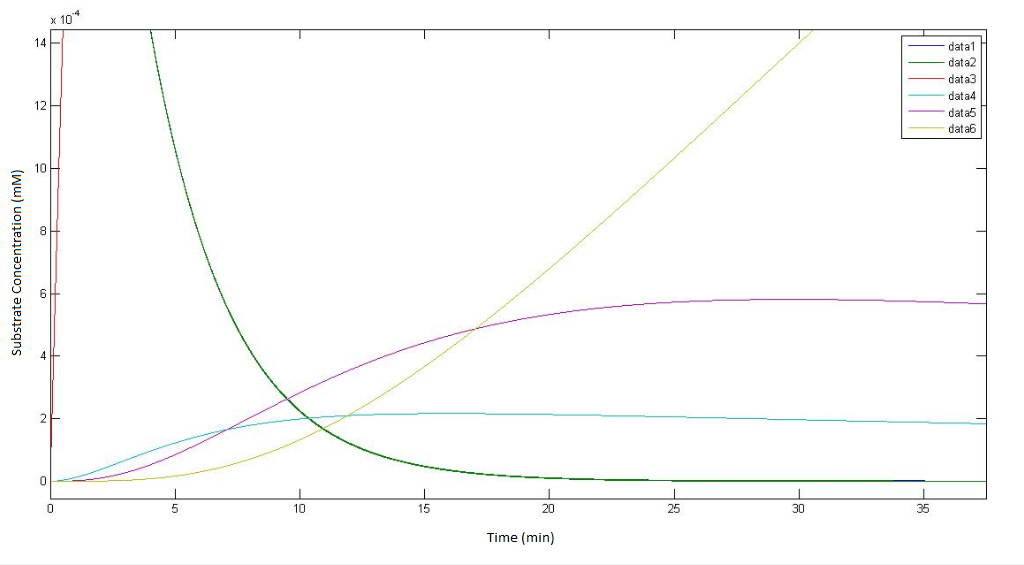
Running the Model

The model was run using MATLAB’s ODE45.

All enzyme concentrations were given a value of 0.1 mM. The temperature was set as T=298K. A plasma membrane distance of d=2nm was given. The cell concentration was given as 1E8 cells/mL. No cellular growth rate was implemented. Glycolate, ε, was left ‘unprocessed’, i.e. it is left to simply accumulate.

Using the constants above the flux took the value:

Assumptions

All enzymes follow MM kinetics as described in the literature.
The enzymes and metabolites are homogeneously distributed within the cell.
The metabolites in the pathway are processed only by the proposed enzymes.
The enzyme concentrations remain constant.
The partition coefficient for DCA in octanol and water is approximately the same as the partition coefficient for the cell membrane.
The cells only grow/divide through DCA-derived-glycolate.
Diffusion can accurately follow
All cells are of the same size (ie equal membrane surface area)

Raw MATLAB code:


function dy = DCA(t,y)
 
dy=zeros(6,1);
 
dy(1)= -6*(10^4)*0.0463067*(y(1)-y(2));
dy(2)= 6*(10^4)*0.0463067*(y(1)-y(2))-3.3*0.1*(y(2)/(0.53+y(2)));
dy(3)= 3.3*0.1*(y(2)/(0.53+y(2)))-0.0871*0.1*(y(3)/(0.94+y(3)));
dy(4)= .0871*0.1*(y(3)/(0.94+y(3)))- 0.6*0.1*(y(4)/(0.16+y(4)));
dy(5)= 0.6*0.1*(y(4)/(0.16+y(4))) - 25.4*0.1*(y(5)/(20+y(5)));
dy(6)= 25.4*0.1*(y(5)/(20+y(5)));
 
end

@@ Line 46: / Line 46: @@
 ===='''Output:'''====
-[[File:Igem regraph_1.jpg|center]]
+[[File:Igem regraph_1.jpg|950px]]
-[[File:Igem regraph_2.jpg|center]]
+[[File:Igem regraph_2.jpg|950px]]
 {{Team:SydneyUni_Australia/Footer}}