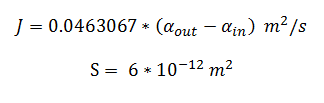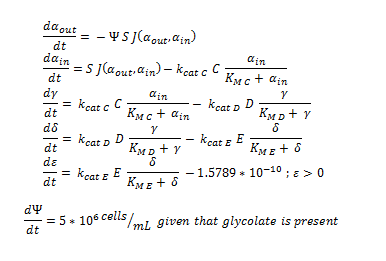Team:SydneyUni Australia/Modelling Output

From 2013.igem.org

(Difference between revisions)
(Created page with "{{Team:SydneyUni_Australia/Style}} {{Team:SydneyUni_Australia/Header}} __NOTOC__ =='''Running the Model'''== The model was run using MATLAB through the ode solver ODE45. Th...")
m (fixed one reference)
 
(27 intermediate revisions not shown)
Line 2: Line 2:
{{Team:SydneyUni_Australia/Header}}
{{Team:SydneyUni_Australia/Header}}
-
__NOTOC__
+
__TOC__
-
=='''Running the Model'''==
 
 +
==Running the Model==
-
The model was run using MATLAB through the ode solver ODE45.
 
 +
The model was run using MATLAB through the ODE solver ODE45.
-
The modelling for both the pathays had initial conditions of:
+
===='''initial conditions'''':====
<center>
<center>
{| class="wikitable"
{| class="wikitable"
Line 53: Line 53:
|-
|-
-
|A, B, C, D, E || 25.55 mM || Estimation from literature [11], as described in "principles".  
+
|A, B, C, D, E || 25.55 mM || Estimation from literature [10], as described in [https://2013.igem.org/Team:SydneyUni_Australia/Modelling_Validation#protein Validation].  
|-
|-
Line 62: Line 62:
-
Physical conditions: the model assumes that the cells are present in minimal media prior to DCA exposure and that the DCA is instantaneously and evenly present at time = 0 min in a solution of homogeneously mixed cells
+
===='''Physical conditions:'''====
-
Many assumptions have been made in the construction of the model and are outlined in the 'principles' section.
+
The model assumes that the cells are present in minimal media prior to DCA exposure and that the DCA is instantaneously and evenly present at time = 0 min in a solution of homogeneously mixed cells.
-
 
+
Many other assumptions have been made in the construction of the model and are outlined in the [https://2013.igem.org/Team:SydneyUni_Australia/Modelling_Model mathematical model] section.
-
 
+
 +
===='''Flux rate:'''====
By using the constants summarised in the previous section the flux, J, took the value (alongside the bacterial surface area, S):
By using the constants summarised in the previous section the flux, J, took the value (alongside the bacterial surface area, S):
-
[[File: my spoon is too big.png|270px]]
+
[[File: my spoon is too big.png|270px|center]]
-
 
+
-
 
+
Line 77: Line 75:
-
=='''The Non-monooxygenase Pathway'''==
+
==The Non-monooxygenase Pathway==
-
'''ODE overview:'''
+
====Summary of the ODE:====
[[File:Igem ode 111.png|center]]
[[File:Igem ode 111.png|center]]
-
The summary of the ODE (explained and justified in the previous section).
+
This system of ODE has been explained and justified in the [https://2013.igem.org/Team:SydneyUni_Australia/Modelling_Model#ODE previous section]. It has been converted into MATLAB code in order to run the model, allowing a computer to generate the graphs below.  
-
'''Raw MATLAB code:'''
+
====Raw MATLAB code:====
  <nowiki>
  <nowiki>
Line 124: Line 122:
-
===='''MATLAB output:'''====
+
====MATLAB output:====
-
 
+
 +
<div id="graph1"></div>
'''The rate at which DCA is removed in solution:'''
'''The rate at which DCA is removed in solution:'''
[[File: DCAcominin.png|950px]]
[[File: DCAcominin.png|950px]]
-
Graph 1: The blue line represents how the concentration of DCA in solution (extracellular) decreases due to the action of our DCA degraders. The red line represents the intracellular concentions of the metabolites (disregard in this graph). One can see that an initial concentration of 2E8 cells/mL completely removes the DCA with a concentration 1mM in (roughly) 150mins.
+
'''Graph 1''': The blue line represents how the concentration of DCA in solution (extracellular) decreases due to the action of our DCA degraders. One can see that an initial concentration of 2 x 10<sup>8</sup> cells/mL completely removes the DCA with a concentration 1 mM in (roughly) 150 min.
-
 
+
-
'''The Rate at which the intracellular concentration of the metabolites change over time:'''
+
<div id="graph2"></div>
 +
'''The rate at which the intracellular concentration of the metabolites change over time:'''
[[File: intermediates1111.png|950px]]
[[File: intermediates1111.png|950px]]
-
Graph 2: Each line represents the concentration of each of the metabolites . This graph is simply a rescaling of graph 1. Note: the glycolate won’t accumulate in the cell – it is metabolised – the model had glycolate as the final product. It is used to show that the presence of glycolate can attribute to cell growth.
+
'''Graph 2''': Each line represents the concentration of each of the metabolites. This graph is simply a rescaling of graph 1. Note: the glycolate won’t accumulate in the cell because it is metabolised. The model had glycolate as the final product and can be used to show how the presence of glycolate can lead to cell growth.
Line 146: Line 144:
-
'''Rescaling the graph once again: the rate at which the metabolic intermediate change over time.'''
+
<div id="graph3"></div>
 +
'''Rescaling the graph once again: the rate at which the metabolic intermediates change over time.'''
[[File: intermediates2222.png|950px]]
[[File: intermediates2222.png|950px]]
-
Graph 3: Each line represents the concentration of each of the metabolites . This graph is simply a rescaling of graph 1 and 2.
+
'''Graph 3''': Each line represents the concentration of each of the metabolites . This graph is simply a rescaling of graph 1 and 2.
 +
<div id="graph4"></div>
'''The rate at which the cells grow over time:'''
'''The rate at which the cells grow over time:'''
[[File: cellscellscells.png|950px]]
[[File: cellscellscells.png|950px]]
-
Graph 4: the blue line represents the linear increase of cells due to the presence of intracellular glycolate.  
+
'''Graph 4''': the blue line represents the linear increase of cells due to the presence of intracellular glycolate.  
Line 168: Line 168:
-
=='''The Non-monooxygenase Pathway'''==
 
-
'''ODE overview''':
+
==The Monooxygenase Pathway==
-
[[File: Igem_ode_22.png|450px]]
 
 +
====ODE overview:====
 +
 +
[[File: Igem_ode_22.png|450px]]
 +
 +
Again, this system of ODE has been explained and justified in the [https://2013.igem.org/Team:SydneyUni_Australia/Modelling_Model#ODE previous section]. Below it is converted to MATLAB, allowing a computer to generate a visual representation of the model.
-
'''Raw MATLAB code:'''
+
====Raw MATLAB code:====
  <nowiki>
  <nowiki>
Line 213: Line 216:
-
'''MATLAB output:'''
+
====MATLAB output:====
-
 
+
 +
<div id="graph5"></div>
'''The rate at which DCA is removed in solution:'''
'''The rate at which DCA is removed in solution:'''
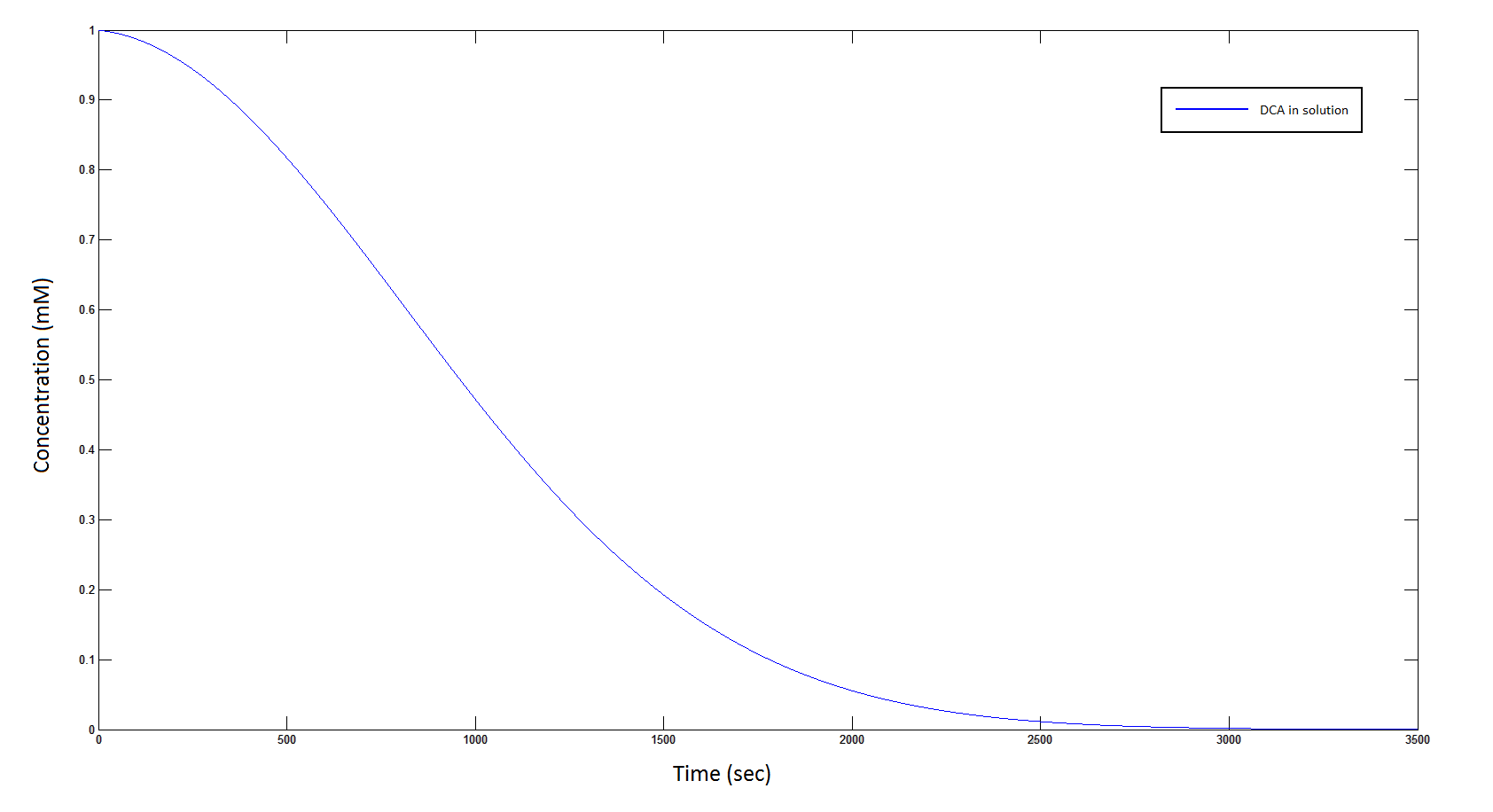
[[File: DCAcominin1.png|950px]]
[[File: DCAcominin1.png|950px]]
-
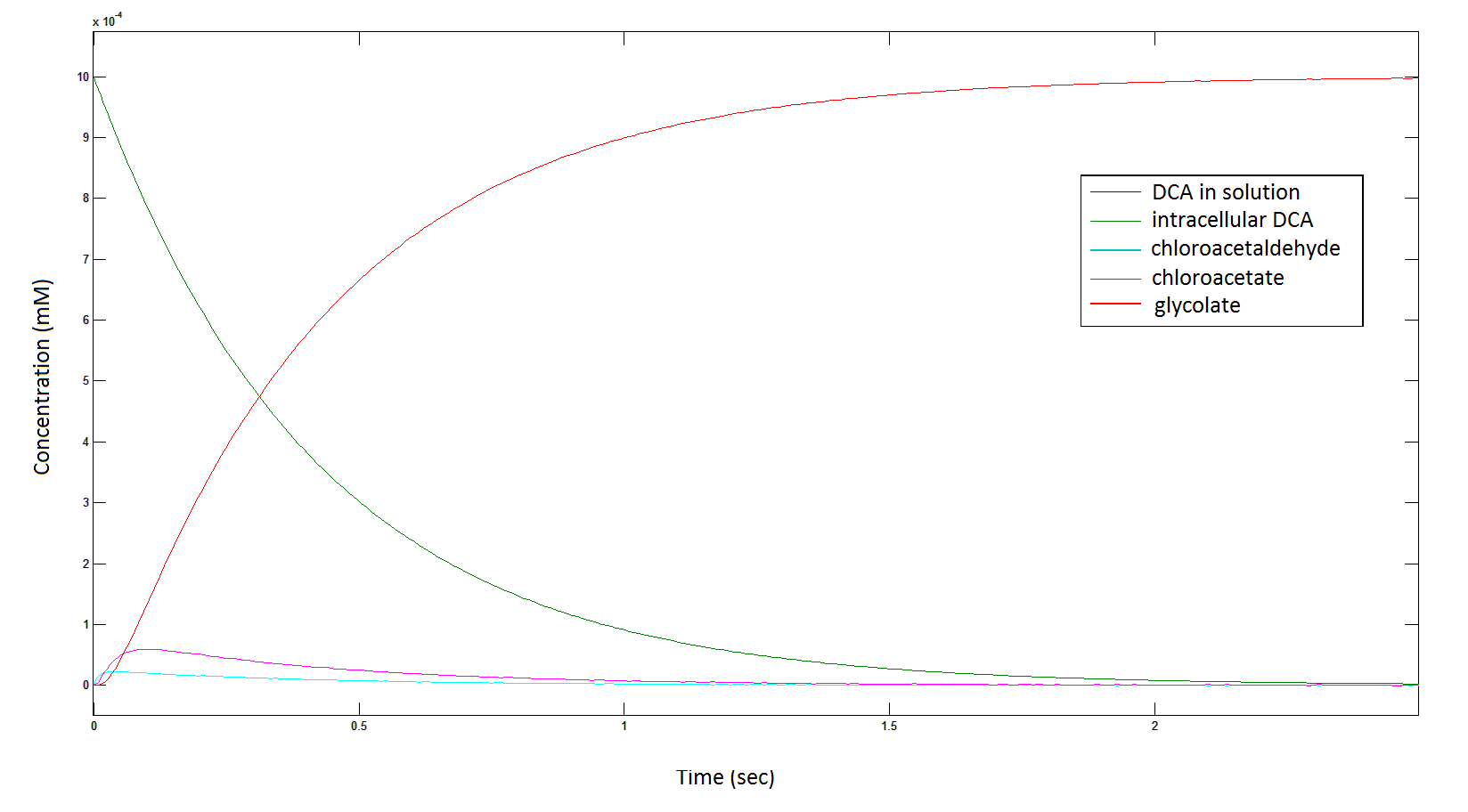
Graph 5: The blue line represents how the concentration of DCA in solution (extracellular) decreases due to the action of our DCA degraders.  
+
'''Graph 5''': The blue line represents how the concentration of DCA in solution (extracellular) decreases due to the action of our DCA degraders.  
-
 
+
-
'''The Rate at which the intracellular concentration of the metabolites change over time:'''
+
<div id="graph6"></div>
 +
'''The rate at which the intracellular concentration of the metabolites change over time:'''
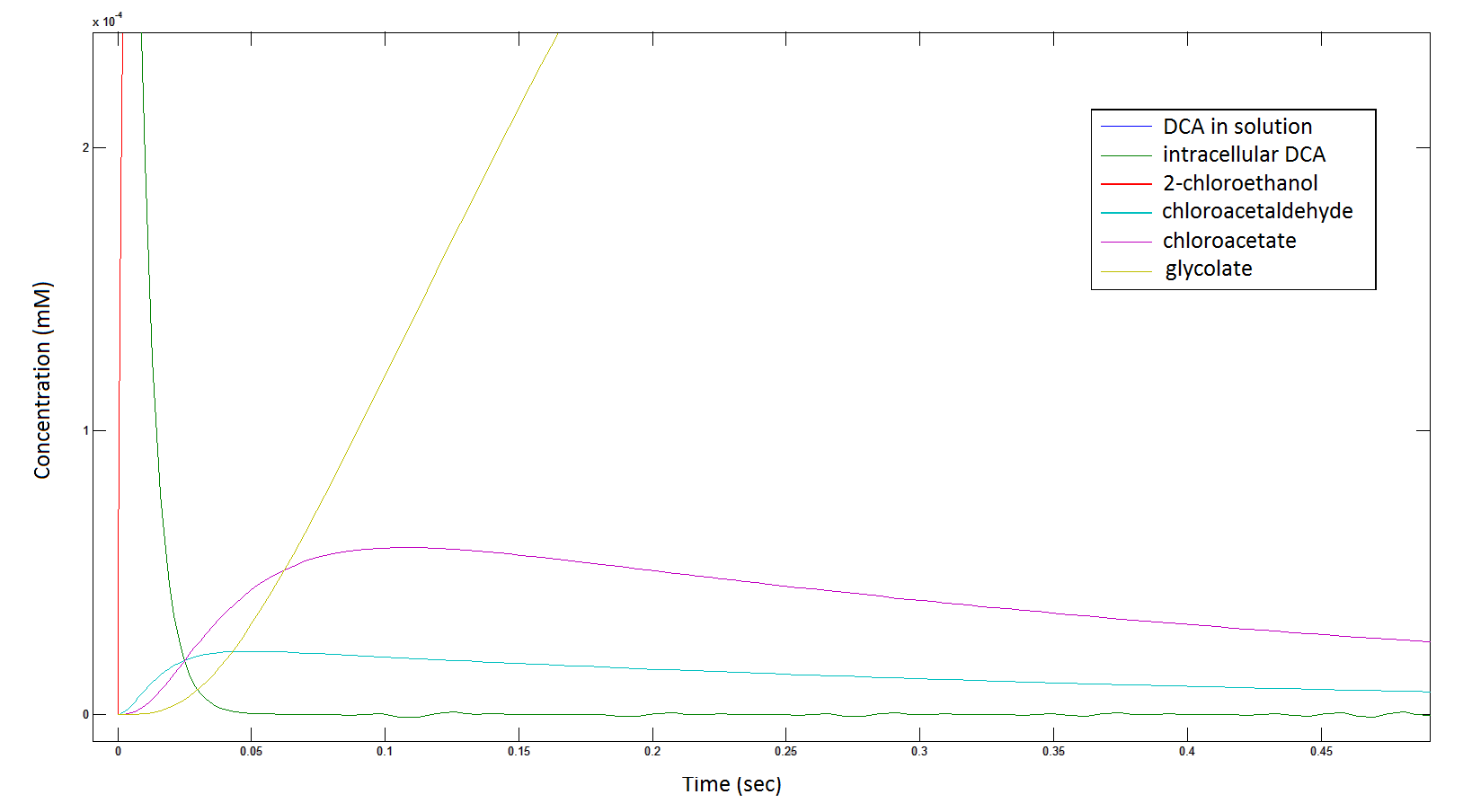
[[File: intermediates111.png|950px]]
[[File: intermediates111.png|950px]]
-
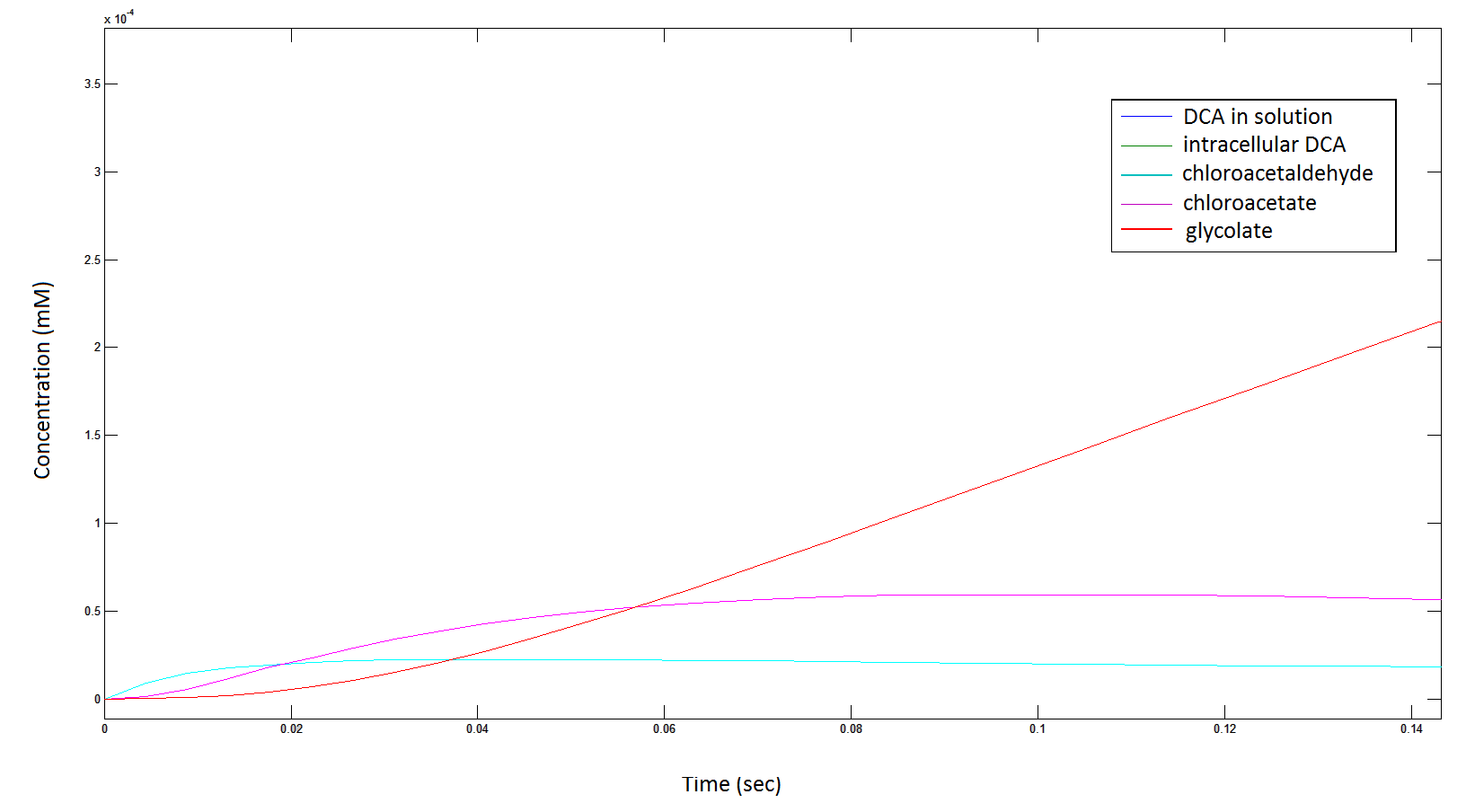
Graph 6: Each line represents the intracellular concentration of each of the metabolites over time within a single cell. The colour associated with each metabolite is depicted in the figure legend. This graph is simply a rescaling of graph 5.
+
'''Graph 6''': Each line represents the intracellular concentration of each of the metabolites over time within a single cell. The colour associated with each metabolite is depicted in the figure legend. This graph is simply a rescaling of graph 5.
Line 237: Line 240:
 +
<div id="graph7"></div>
'''Rescaling the graph once again: the rate at which the metabolic intermediate change over time.'''
'''Rescaling the graph once again: the rate at which the metabolic intermediate change over time.'''
[[File: thismessagewasbroughttoyoubuygoontheproudsponserofthismodel.png|950px]]
[[File: thismessagewasbroughttoyoubuygoontheproudsponserofthismodel.png|950px]]
-
Graph 7: Again, each line represents the intracellular concentration of each of the metabolites over time within a single cell. This graph is simply a rescaling of graph 5 and 6.
+
'''Graph 7''': Again, each line represents the intracellular concentration of each of the metabolites over time within a single cell. This graph is simply a rescaling of graph 5 and 6.
Line 247: Line 251:
 +
 +
<div id="graph8"></div>
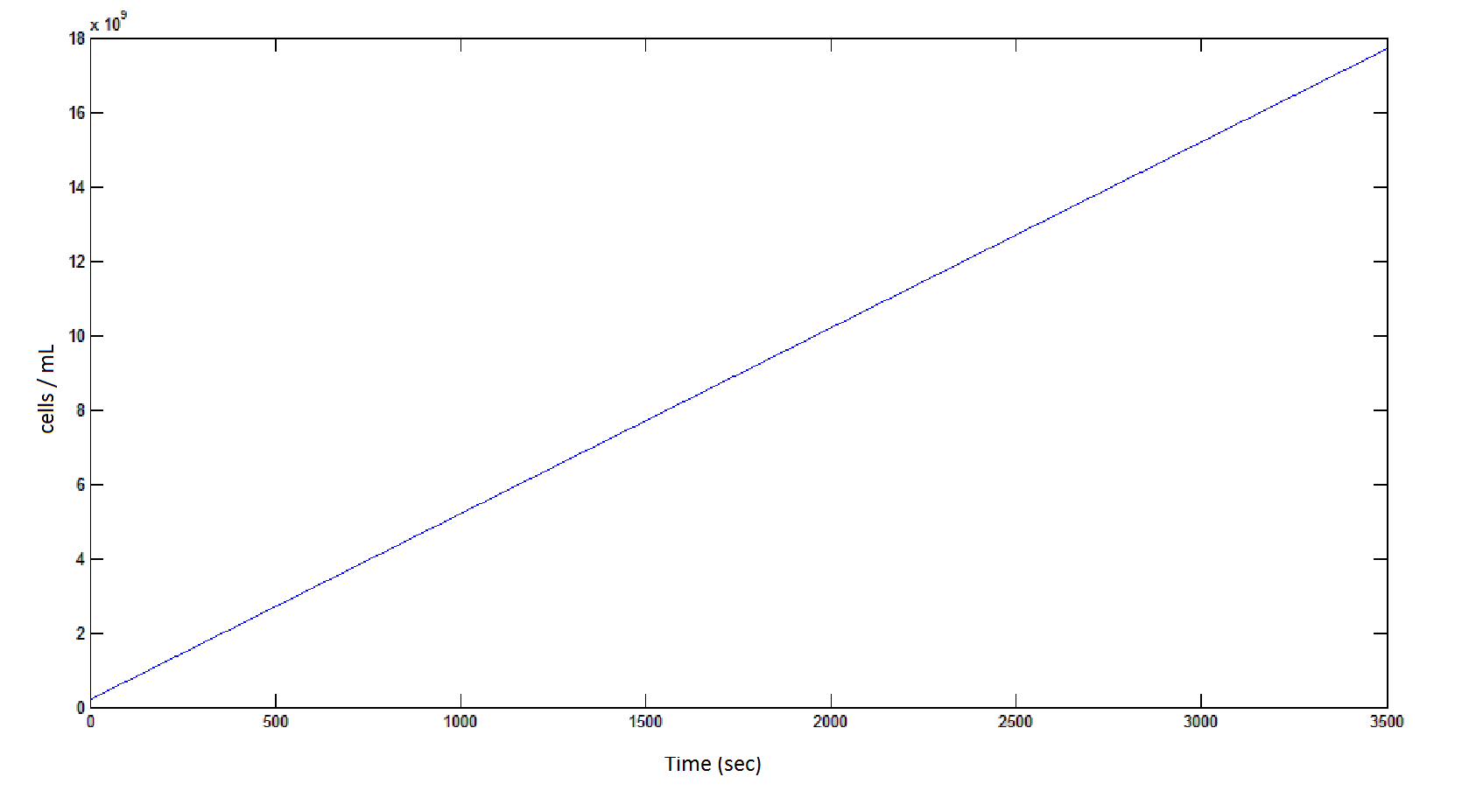
'''The rate at which the cells grow over time:'''
'''The rate at which the cells grow over time:'''
[[File: cellscellscelllls.png|950px]]
[[File: cellscellscelllls.png|950px]]
-
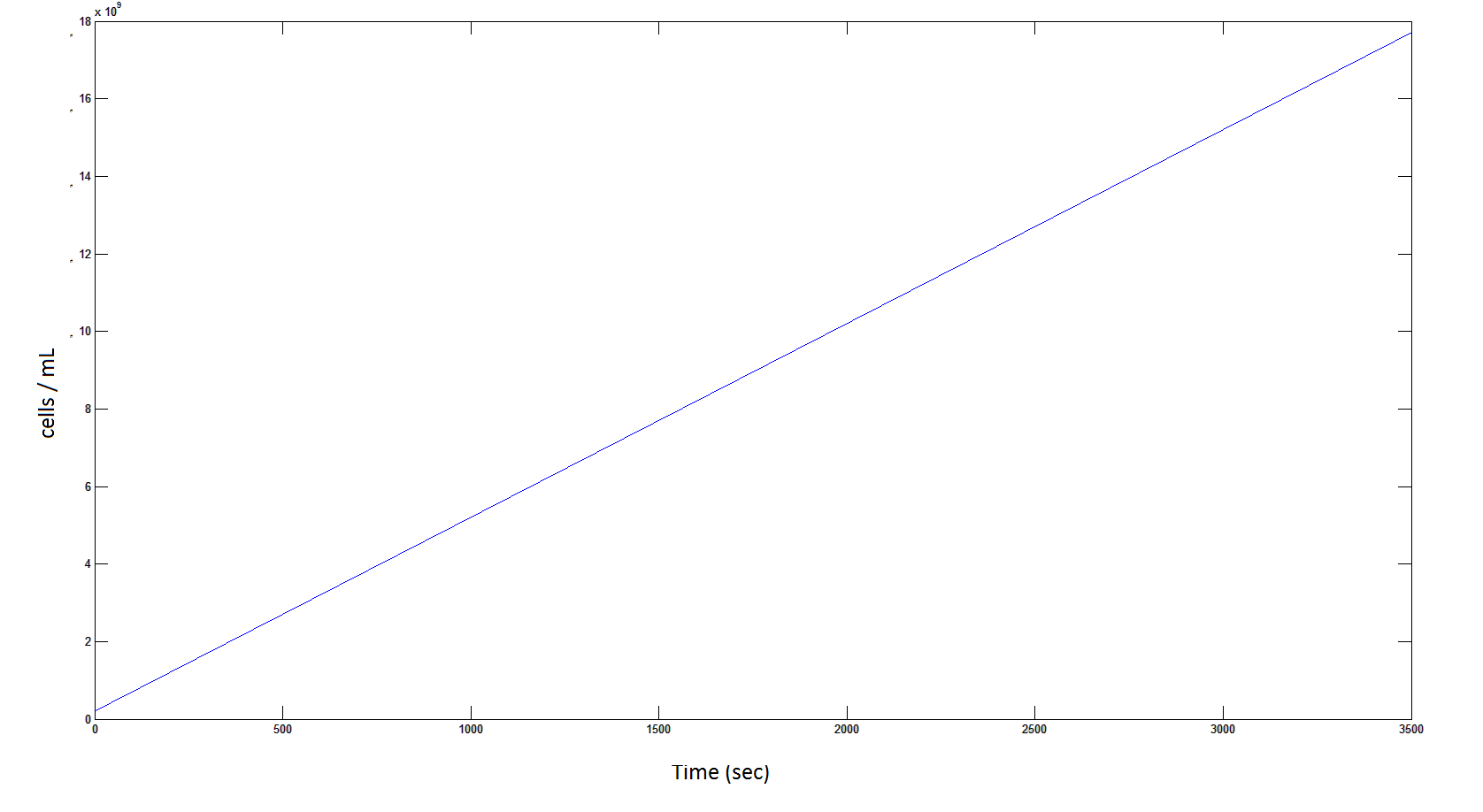
Graph 8: The blue line represents the linear increase of the total number of cells due to the presence of intracellular glycolate.  
+
'''Graph 8''': The blue line represents the linear increase of the total number of cells due to the presence of intracellular glycolate.  
Line 257: Line 263:
-
'''Rescaling Shows a lag effect on cell growth:'''
+
 
 +
<div id="graph9"></div>
 +
'''Rescaling shows a lag effect on cell growth:'''
[[File: cellscellscelllllllllllls.png|950px]]
[[File: cellscellscelllllllllllls.png|950px]]
-
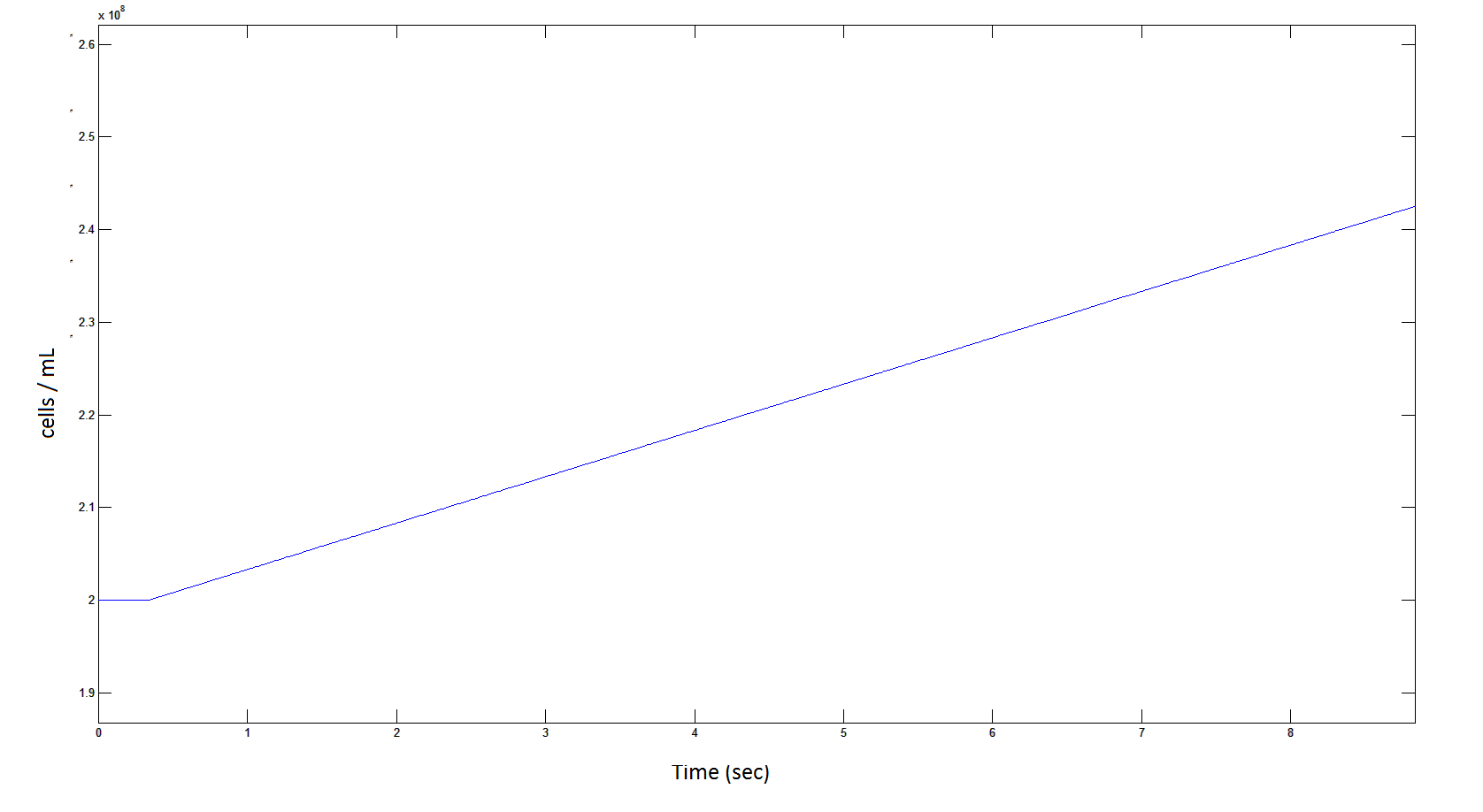
Graph 9: The blue line represents the increase of cells due to the presence of intracellular glycolate. This graph is a rescaling of graph 8 to show the inital lag in cellualr growth.
+
'''Graph 9''': The blue line represents the increase of cells due to the presence of intracellular glycolate. This graph is a rescaling of graph 8 to show the initial lag in cellular growth.
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
== '''Conclusions:''' ==
+
-
 
+
-
From Graphs 1 and 5, one can see that 1mM of DCA is removed from solution within roughly 50 minutes when the DCA degrading cells are at a concentration of 2E8 cells/mL.
+
-
 
+
-
From Graphs 4, 8 and 9, it is evident that bacterial growth occurs. This growth is due to the production of glycolate, and by comparing graphs 6 and 9, one can see that bacterial growth correlates with glycolate accumulation.
+
-
 
+
-
The cytotoxic metabolic intermediate chloroactealdehyde doesn't accumulate to a significant concentration in any of the pathways and is consistently at a negligibly small concentration. From Graphs 3 and 7 one can see that chloroacetaldehyde reaches a maximum concentration of roughly 0.2 mM in both pathways. Chloroacetaldehyde is seen to be metabolised very quickly; this concentration maximum is very short lived where it peaks at roughly 0.03 seconds and returns back to 0 mM by 0.5 seconds. It is expected that chloroacetaldehyde toxicity will not be a problem in our engineered cells.
+
-
 
+
-
It is also possible to conclude that the pathways remove DCA at the same rate (through comparing graphs 1 and 5).
+
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
 
+
-
== '''References:''' ==
+
-
 
+
-
[1] Krooshof, G. H., Ridder, I. S., Tepper, A. W., Vos, G. J., Rozeboom, H. J., Kalk, K. H., Dijkstra, B. W. & Janssen, D. B. (1998). Kinetic Analysis and X-ray Structure of Haloalkane Dehalogenase with a Modified Halide-Binding Site. <i>Biochemistry</i>, <b>37</b>(43), 15013-15023.
+
-
 
+
-
[2]  Janecki, D. J., Bemis, K. G., Tegeler, T. J., Sanghani, P. C., Zhai, L., Hurley, T. D., Bosron, W. F. & Wang, M. (2007). A multiple reaction monitoring method for absolute quantification of the human liver alcohol dehydrogenase ADH1C1 isoenzyme. <i>Analytical Biochemistry</i>, <b>369</b>(1), 18-26.
+
-
 
+
-
[3] Pandey, A. V. & Flück, C. E. (2013). NADPH P450 oxidoreductase: Structure, function, and pathology of diseases. <i>Pharmacology & Therapeutics</i>, <b>138</b>(2), 229-254.
+
-
 
+
-
[4]  van der Ploeg, J., Shmidt, M. P., Landa, A. S., & Janssen, D. B. (1994). Identification of Chloroacetaldehyde Dehydrogenase Involved in 1,2-Dichloroethane Degradation. <i>Applied Environmental Microbiology</i> <b>60</b>(5), 1599-1605.
+
-
 
+
-
[5]  van der Ploeg, J., van Hall, G. & Janssen, D. B. (1991) Characterization of the haloacid dehalogenase from Xanthobacter autotrophicus GJ10 and sequencing of the dhlB gene. <i>Journal of Bacteriology</i>, <b>173</b>(24), 7925-33.
+
-
 
+
-
[6] Sinensky, M. I. (1974). Homeoviscous Adaption – A Homeostatic Process that Regulates the Viscosity of Membrane Lipids in <i>Escherichia coli</i>. <i>Proceedings from the National Academy of Science of the United States of America</i>, <b>71</b>(2), 522-525.
+
-
 
+
-
[7] CyberCell Database
+
-
 
+
-
[8]
+
-
 
+
-
[9]
+
-
[10] http://www.dtsc.ca.gov/AssessingRisk/Upload/12dca.pdf
 
-
[11] Ishihama, Y., Schmidt, T., Rappsilber, J., Mann, M., Hartl F. U., Kerner, M. J. & Frishman, D. (2008) Protein abundance profiling of the Escherichia coli cytosol. BMC Genomics, <b>9</b>:102
 
-
[12] Lord, J. M. (1972) Glycolate oxidoreductase in Escherichia coli. Biochemica et Biophysica Acta <b>267</b>:2, 227-327.
 
{{Team:SydneyUni_Australia/Footer}}
{{Team:SydneyUni_Australia/Footer}}

Latest revision as of 00:42, 29 October 2013

SydneyUniversity Top Banner.jpg SydneyUniversity Bottom Banner.jpg

Contents


Running the Model

The model was run using MATLAB through the ODE solver ODE45.

initial conditions':

Constant Value Comment
KM A 0.530 mM From literature [1]
kcat A 3.3 s-1 From literature [1]
KM B 0.940 mM From literature [2]
kcat B 0.0871 s-1 From literature [2]
KM C 7.2 mM From literature [3]
kcat c 89.8 s-1 From literature [3]
KM D 0.160 mM From literature [4]
kcat D 0.600 s-1 From literature [4]
KM E 20 mM From literature [5]
kcat E 25.4 s-1 From literature [5]
β, γ, δ & ε 0 mM Not naturally present in cells.
αout 1 mM Initial concentration of DCA in solution (arbitrary)
αin 0.001 mM Initial concentration of DCA in cell
A, B, C, D, E 25.55 mM Estimation from literature [10], as described in Validation.
2 x 108 cells / mL Initial cell concentration which allows appropriate growth


Physical conditions:

The model assumes that the cells are present in minimal media prior to DCA exposure and that the DCA is instantaneously and evenly present at time = 0 min in a solution of homogeneously mixed cells. Many other assumptions have been made in the construction of the model and are outlined in the mathematical model section.

Flux rate:

By using the constants summarised in the previous section the flux, J, took the value (alongside the bacterial surface area, S):

My spoon is too big.png



The Non-monooxygenase Pathway

Summary of the ODE:

Igem ode 111.png

This system of ODE has been explained and justified in the previous section. It has been converted into MATLAB code in order to run the model, allowing a computer to generate the graphs below.

Raw MATLAB code:


function dy = nop450(t,y)
 
dy=zeros(7,1);
 
dy(1)= -y(7)*(6*10^(-12))*0.0463067*(y(1)-y(2));
dy(2)= ((6*10^(-12))*0.0463067*(y(1)-y(2)))-3.3*25.55*(y(2)/(0.53+y(2)));
dy(3)= 3.3*25.55*(y(2)/(0.53+y(2)))-0.0871*25.55*(y(3)/(0.94+y(3)));
dy(4)= .0871*25.55*(y(3)/(0.94+y(3)))- 0.6*25.55*(y(4)/(0.16+y(4)));
dy(5)= 0.6*25.55*(y(4)/(0.16+y(4))) - 25.4*25.55*(y(5)/(20+y(5)));
 
   if y(6) >  2*10^(-10)
      dy(6)= 25.4*25.55*(y(5)/(20+y(5))) -1.5789*10^(-10)
   else
       dy(6) = 25.4*25.55*(y(5)/(20+y(5)))
   end
   
   if y(6) > 0.0005 
        if y(7) > 1.6*10^11
            dy(7)=0
        else
            dy(7) = 5*10^6
        end
   else
        dy(7) = 0
   end
 
end



MATLAB output:

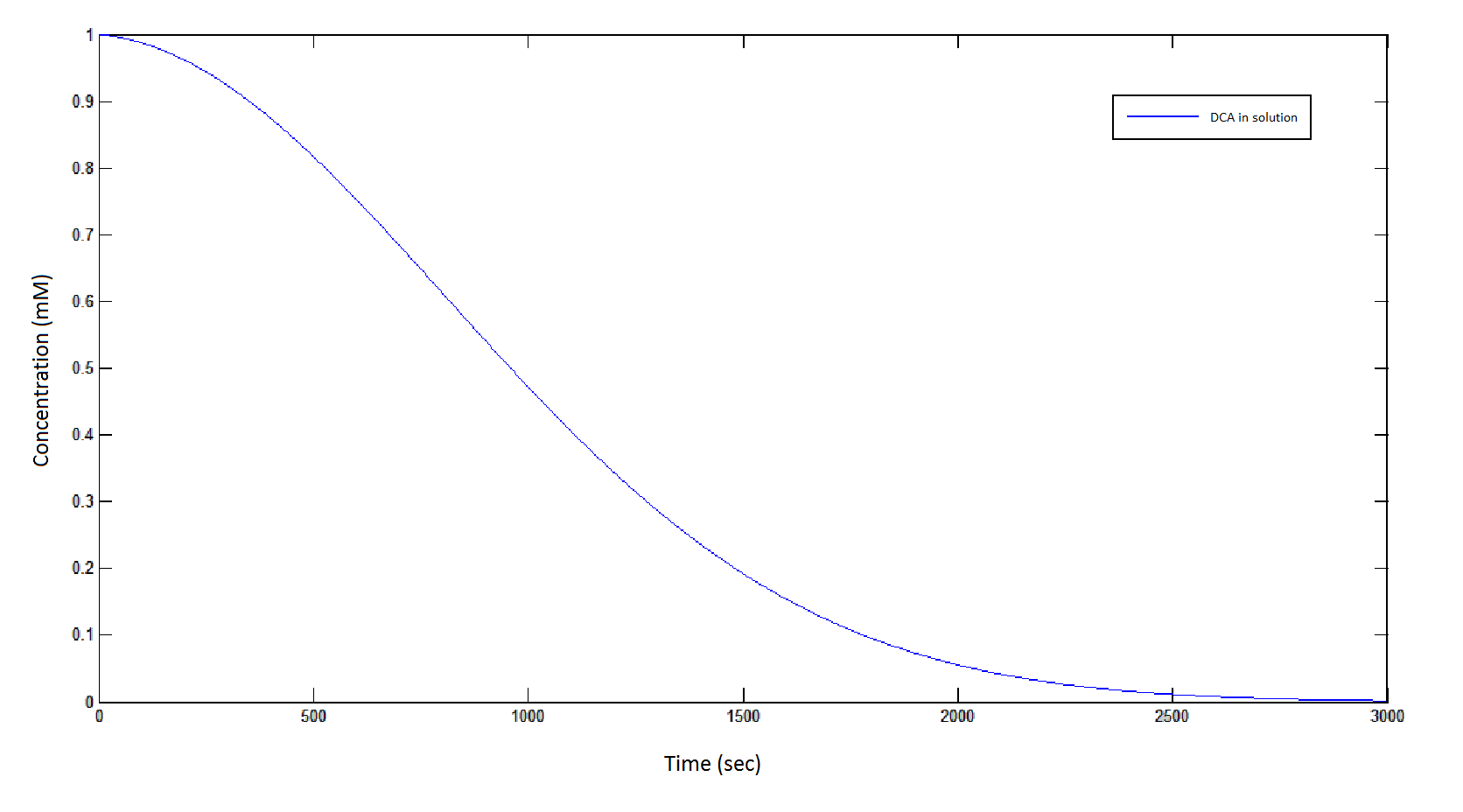
The rate at which DCA is removed in solution:

DCAcominin.png

Graph 1: The blue line represents how the concentration of DCA in solution (extracellular) decreases due to the action of our DCA degraders. One can see that an initial concentration of 2 x 108 cells/mL completely removes the DCA with a concentration 1 mM in (roughly) 150 min.


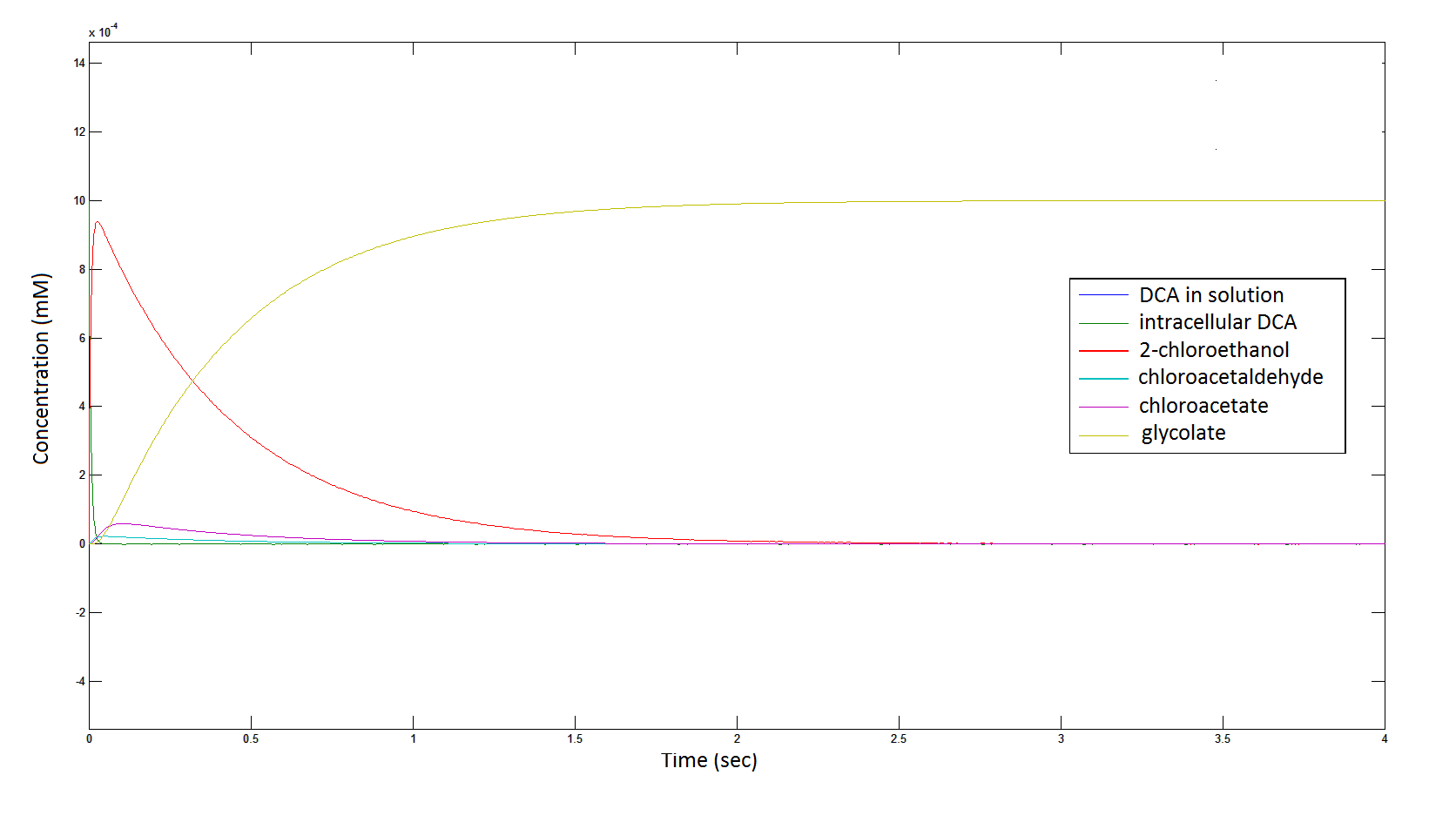
The rate at which the intracellular concentration of the metabolites change over time:

Intermediates1111.png

Graph 2: Each line represents the concentration of each of the metabolites. This graph is simply a rescaling of graph 1. Note: the glycolate won’t accumulate in the cell because it is metabolised. The model had glycolate as the final product and can be used to show how the presence of glycolate can lead to cell growth.



Rescaling the graph once again: the rate at which the metabolic intermediates change over time.

Intermediates2222.png

Graph 3: Each line represents the concentration of each of the metabolites . This graph is simply a rescaling of graph 1 and 2.



The rate at which the cells grow over time:

Cellscellscells.png

Graph 4: the blue line represents the linear increase of cells due to the presence of intracellular glycolate.






The Monooxygenase Pathway

ODE overview:

Igem ode 22.png

Again, this system of ODE has been explained and justified in the previous section. Below it is converted to MATLAB, allowing a computer to generate a visual representation of the model.

Raw MATLAB code:

function dy = p450(t,y)
 
dy=zeros(6,1);
 
dy(1)= -y(6)*(6*10^(-12))*0.0463067*(y(1)-y(2));
dy(2)= ((6*10^(-12))*0.0463067*(y(1)-y(2))) - 0.0113*25.55*(y(2)/(.12+y(2)));
dy(3) = 0.0113*25.55*(y(2)/(.12+y(2))) - 0.6*25.55*(y(3)/(0.16+y(3)));
dy(4)= 0.6*25.55*(y(3)/(0.16+y(3))) - 25.4*25.55*(y(4)/(20+y(4)));
 
 
   if y(5) >  2*10^(-10)
      dy(5)= 25.4*25.55*(y(4)/(20+y(4))) -1.5789*10^(-10)
   else
       dy(5) = 25.4*25.55*(y(4)/(20+y(4)))
   end
   
   if y(5) > 0.0005 
        if y(6) > 1.6*10^11
            dy(6)=0
        else
            dy(6) = 5*10^6
        end
   else
        dy(6) = 0
   end
 
end


MATLAB output:

The rate at which DCA is removed in solution:

DCAcominin1.png

Graph 5: The blue line represents how the concentration of DCA in solution (extracellular) decreases due to the action of our DCA degraders.



The rate at which the intracellular concentration of the metabolites change over time:

Intermediates111.png

Graph 6: Each line represents the intracellular concentration of each of the metabolites over time within a single cell. The colour associated with each metabolite is depicted in the figure legend. This graph is simply a rescaling of graph 5.



Rescaling the graph once again: the rate at which the metabolic intermediate change over time.

Thismessagewasbroughttoyoubuygoontheproudsponserofthismodel.png

Graph 7: Again, each line represents the intracellular concentration of each of the metabolites over time within a single cell. This graph is simply a rescaling of graph 5 and 6.




The rate at which the cells grow over time:

Cellscellscelllls.png

Graph 8: The blue line represents the linear increase of the total number of cells due to the presence of intracellular glycolate.




Rescaling shows a lag effect on cell growth:

Cellscellscelllllllllllls.png

Graph 9: The blue line represents the increase of cells due to the presence of intracellular glycolate. This graph is a rescaling of graph 8 to show the initial lag in cellular growth.



With thanks to:



Retrieved from "http://2013.igem.org/Team:SydneyUni_Australia/Modelling_Output"