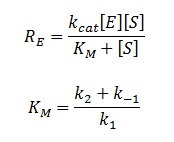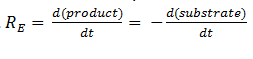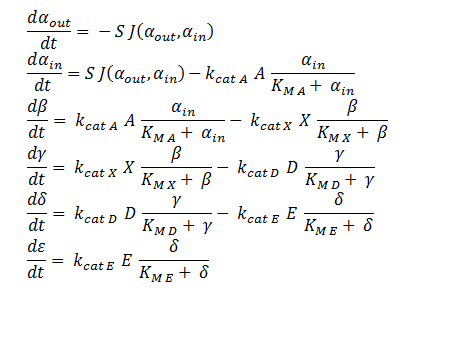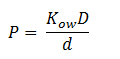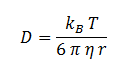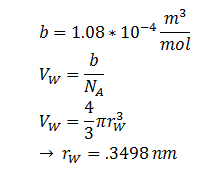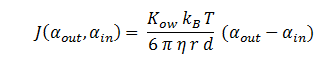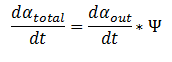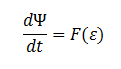Team:SydneyUni Australia/Modelling Principles
From 2013.igem.org
| Line 6: | Line 6: | ||
=='''A Brief Background on Michaelis-Menton Kinetics'''== | =='''A Brief Background on Michaelis-Menton Kinetics'''== | ||
| - | The majority of single-substrate metabolic enzymes follow MM kinetics, for which the equations accurately describe enzyme activity. The system is based on the forward and reverse kinetic rate (k<sub>1</sub> and k<sub>-1</sub> respectively) of substrate-enzyme binding followed by the irreversible catalytic step of product formation (k<sub>2</sub>) as depicted in the figure below: | + | |
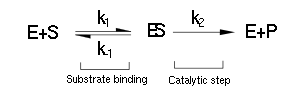
| + | <div align="justify">The majority of single-substrate metabolic enzymes follow MM kinetics, for which the equations accurately describe enzyme activity. The system is based on the forward and reverse kinetic rate (k<sub>1</sub> and k<sub>-1</sub> respectively) of substrate-enzyme binding followed by the irreversible catalytic step of product formation (k<sub>2</sub>) as depicted in the figure below: | ||
| + | </div> | ||
[[File:Igem pathway 1.png|center]] | [[File:Igem pathway 1.png|center]] | ||
| Line 12: | Line 14: | ||
[[File:Igem Re.jpg|center]] | [[File:Igem Re.jpg|center]] | ||
| - | The rate of catalysis for an enzyme is a function of the enzyme and substrate concentration and incorporates the catalytic constant K<sub>cat</sub> and the Michaelis constant K<sub>m</sub>, which are given in most of the literature that involves enzyme kinetics. The symbol denotes the reaction rate: the rate of product formation, i.e. | + | |
| + | <div align="justify"> | ||
| + | The rate of catalysis for an enzyme is a function of the enzyme and substrate concentration and incorporates the catalytic constant K<sub>cat</sub> and the Michaelis constant K<sub>m</sub>, which are given in most of the literature that involves enzyme kinetics. The symbol denotes the reaction rate: the rate of product formation, i.e. </div> | ||
[[File:Igem Re= dproduct.png|center]] | [[File:Igem Re= dproduct.png|center]] | ||
| Line 21: | Line 25: | ||
[[File:pathway_2.png|center]] | [[File:pathway_2.png|center]] | ||
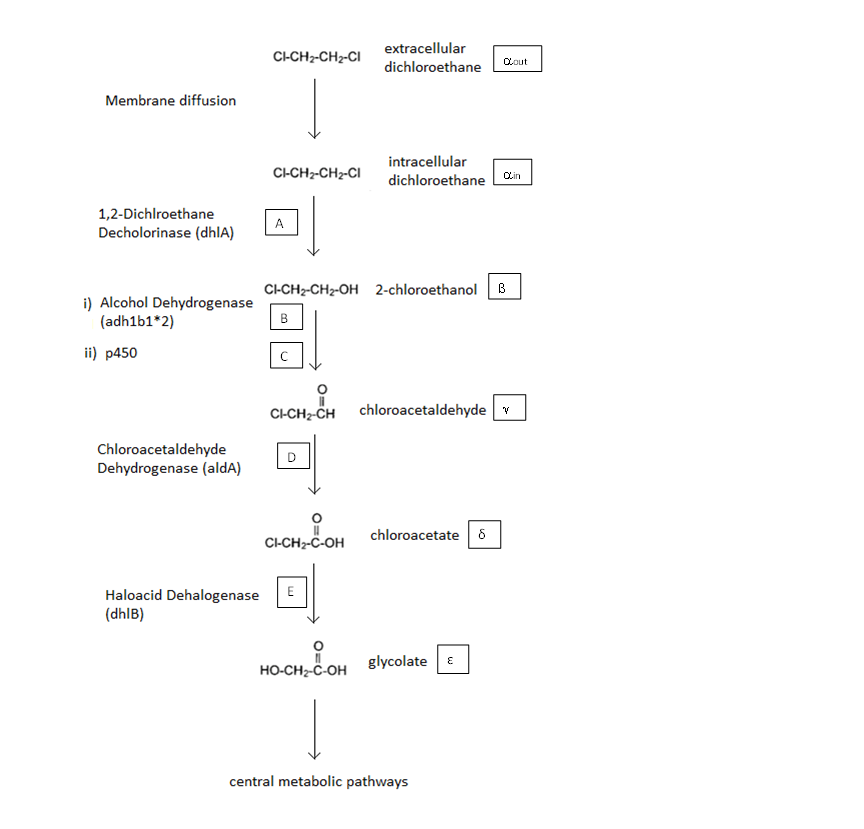
| - | In the above figure the symbols represent the intracellular concentration of the associated metabolite or enzyme.More information is given below | + | |
| + | <div align="justify"> | ||
| + | In the above figure the symbols represent the intracellular concentration of the associated metabolite or enzyme.More information is given below</div> | ||
| Line 108: | Line 114: | ||
=='''Extending the System to Cell Cultures'''== | =='''Extending the System to Cell Cultures'''== | ||
| - | + | <div align="justify">The model can be extended to a homogeneous solution/culture of cells. Let Ψ represent the concentration of the cells in solution. The overall rate of decrease of DCA (αtotal) in solution is | |
| - | The model can be extended to a homogeneous solution/culture of cells. Let Ψ represent the concentration of the cells in solution. The overall rate of decrease of DCA (αtotal) in solution is | + | </div> |
[[File:Igem datot=daout.png|center]] | [[File:Igem datot=daout.png|center]] | ||
| + | <div align="justify"> | ||
By applying this change, the resulting values of α<sub>in</sub>,α<sub>out</sub>, β, γ & δ represent the metabolite concentration across all cells. | By applying this change, the resulting values of α<sub>in</sub>,α<sub>out</sub>, β, γ & δ represent the metabolite concentration across all cells. | ||
| - | Furthermore the cells are expected to grow due to the production of glycolate (which can be used as a carbon source for growth). | + | Furthermore the cells are expected to grow due to the production of glycolate (which can be used as a carbon source for growth). </div> |
[[File:Igem dpsi=f.png|center]] | [[File:Igem dpsi=f.png|center]] | ||
| - | The rate at which ''E. coli'' can grow based on the amount of glycolate is not described in the literature. However one will be able to infer the growth as a function of amount of glycolate, ε, in the cell through experimentation. | + | <div align="justify"> |
| + | The rate at which ''E. coli'' can grow based on the amount of glycolate is not described in the literature. However one will be able to infer the growth as a function of amount of glycolate, ε, in the cell through experimentation.</div> | ||
{{Team:SydneyUni_Australia/Footer}} | {{Team:SydneyUni_Australia/Footer}} | ||
Revision as of 14:03, 27 September 2013


A Brief Background on Michaelis-Menton Kinetics
A Schematic of the Engineered Metabolic Pathway:
General Information regarding the Enzymes Involved in the Metabolic Pathway
| Enzyme | Gene | Symbol | Constants | Substrate | Product | Ref |
|---|---|---|---|---|---|---|
| 1,2-Dichloroethane Dechlorinase | dhlA | A | KM A=0.53mM, kcat A = 3.3 s-1 | DCA | 2-chloroethanol | [1] |
| Alcohol Dehydrogenase | Adhlb 1/2* | B | KM B=0.94 mM, kcat B = 0.0871 s-1 | 2-chloroethanol | chloroacetaldehyde | [2] |
| p450 | ? | C | KM C = 7.2 mM, kcat C = 89.8 s-1 | 2-chloroethanol | chloroacetaldehyde | [3] |
| Chloroacetaldehyde Dehydrogenase | aldA | D | KM D = 0.0.6mM, kcat D = 0.60 s-1 | chloroacetaldehyde | chloroacetate | [4] |
| Haloacetate Dehydrogenase | dhlB | E | KM E= 20 mM, kcat E = 25.4 s-1 | chloroacetate | glycolate | [5] |
* values based on ethanol as a substrate
ODE Model
The symbols A, X, D & E represent the intracellular enzyme concentrations, where X = B or C, and the symbols αin,αout, β, γ & δ represent the concentrations of the metabolic intermediates. The function J(αout,αin ) represents the flux of extracellular DCA across the plasma membrane and is a function of the extra and intracellular concentrations of DCA. The value S represents the average surface area of the cellular membrane of E. coli. See below for the derivation of J. The initial conditions for the system are αin=β=γ=δ=0 M at t=0 min, ε=εphys & αout=αout(t=0) . Where is the physiological concentration of non-DCA-derived glycolate and αout(t=0) is the initial concentration of DCA outside of the cellular membrane.
The intracellular enzyme concentrations will be determined experimentally.
DCA Diffusion Across the Plasma Membrane
The diffusion of DCA across the cell membrane was modelled based on Fick’s first law of diffusion:
In Summary, the flux across the membrane is:
| Symbol | Name | Value (units) | Ref |
|---|---|---|---|
| η | Cellular Membrane Viscosity | 1.9 kg/m/s | [6] |
| S | E. coli Membrane Surface Area | 6E-12 m2 | [7] |
| r | DCA radius | 0.3498 nm | [8] |
| Kow | Octanol-water Partition Coefficient for DCA | 28.2 | [9] |
| d | Length of Cellular Membrane | ??? | [10] |
Extending the System to Cell Cultures
By applying this change, the resulting values of αin,αout, β, γ & δ represent the metabolite concentration across all cells.
Furthermore the cells are expected to grow due to the production of glycolate (which can be used as a carbon source for growth).
 "
"