Team:SUSTC-Shenzhen-A/Modeling

From 2013.igem.org

(Difference between revisions)

Revision as of 19:47, 27 September 2013

Home	Team	Official Team Profile	Project	Parts Submitted to the Registry	Modeling	Protocol and notes	Safety and security	Attributions	Human Practice

Modeling

Abstract

Our model is to simulate a cell-cell mutual help system that is inspired by the classic prisoner's dilemma. We use two kinds of operated cells to act as the two prisoners. Both of them are facing the same problem comes from the environment, if they do not help each other, both of them will get into a terrible situation. Even they choose to collaborate, one may also take the risk that another man would turn traitor to him. So it’s a complex problem that how do our prisoners to choose their strategy to make themselves survive. Here are all equations and variables we have worked out.

So, how can our system perform this prisoner’s dilemma?

We use the growth rate and the concentration of the cells to describe the living status of two prisoners, use Zeocin in our system to represent the punishment on our prisoners, and use the tetA(which will translate companying with the expressing of AHL) to bring Ni into the cells referring to the risk the as telling the lie. And if one receives the shield from another as sufficient AHL, he will start to produce ZeoR protein which can make him survive the Zeocin.

Here are also some Differences

However, our cell-cell mutual help system also do not all obey the classic prisoners’ dilemma, first of all, one prisoner can only have two certain choices in this traditional question, be honest or crafty. But as we have mentioned before, in our system two cells use AHL to help each other, namely the concentration here stands for the attitude of our cell, well it is right the concentration not the existence of AHL makes sense in our system, so our prisoner have a chance to make an elastic choice, they can decide to what level the cooperation will be put into effect. This important difference makes our system more close to the realistic.

Then one prisoner will never really die in a classic situation, but in ours there exists some possibility that one cell can actually die out which will result in a big crash. This is what we should put our eyes on.

Test

To confirm whether our simulations can work out a good result, we want to test some important parameters to see whether our subsystem can work properly,

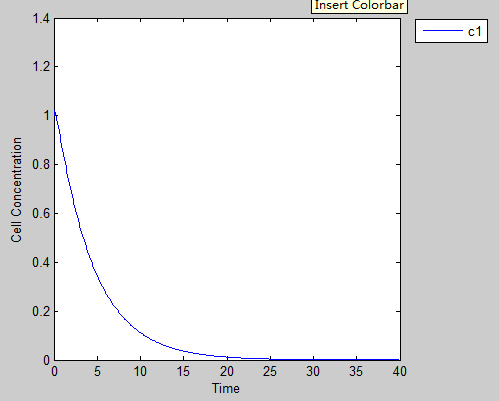
1.the effect of Zeocin

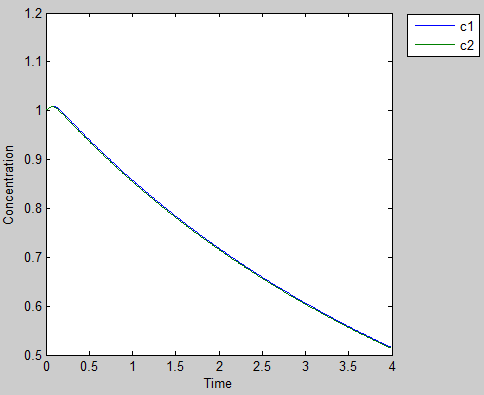
We put our prisoners into a person to see what will happen to this poor man, this will help us understand how powerful the punishment is as well as tell us how much Zeocin we should use to create a temperate environment stress. As we can see from this figure, this antibiotic leads to a quick death of our prisoner. Without help, one man can hardly get out of this problem.

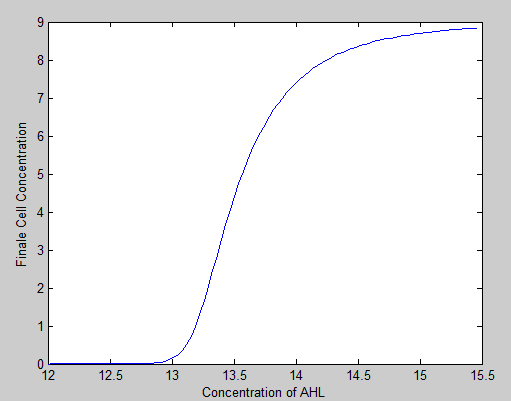
2.separate cell in the environment contain AHL

To test our relationship between the concentration of AHL and the concentration of our cells, we conduct this test. We put one of our prisoners into AHL concentration gradients to make sure where the efficient concentration of AHL lies, and we get the final cell concentration for each AHL gradients.

This EC can tell us some important things such as whether there exists any sensitivity difference of AHL between the two cells, it can help us have a better understanding of the cooperation between these two cells. As we can see there is a cliffy slope in our data, which give us the idea that the relationship between the AHL and cell concentration is not simply linear, so we should consider twice before we change this influential variable.

3.the show begins

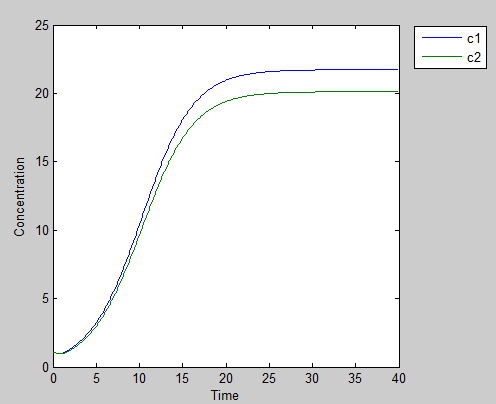
Result 1:Good Cooperation

If both of our prisoners try to help each other things will be much better

Result 2: a Traitor

If one of our prisoners wants to get other help without offering any reward, he may be well benefited at first, but as his partner gets into trouble, he will lose his luck. This though go against the realistic, we can also take well advantage of this flaw in our safety idea. (In the four cases of prisoners’ dilemma there are three cases that the bad man can escape but in our model only if they are well cooperate with each other then they will have chance to run away, but such a good cooperate cannot be easily achieved especially outside the Lab)

Result 3: The Egoists

If both guys are imaginary smart, and have a strong believe that his partner will forswear for him, it’s obvious that they will get deserved penalty.

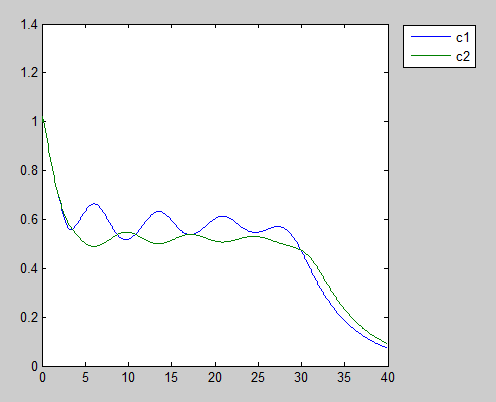
Some more interesting results

The results all above are just considering the same situation that both the prisoners have a similar personality, that says our two cells have a very symmetry structure, their physiological parameters are nearly the same. Basing on this, every cell can act the same behavior when meet the same change in the environment.

However, two pieces of leaves will never coincide in the world. We can’t adjust everything to meet our plan and this considerable material difference gives us the opportunity to have a sight of the real prisoner’s dilemma.

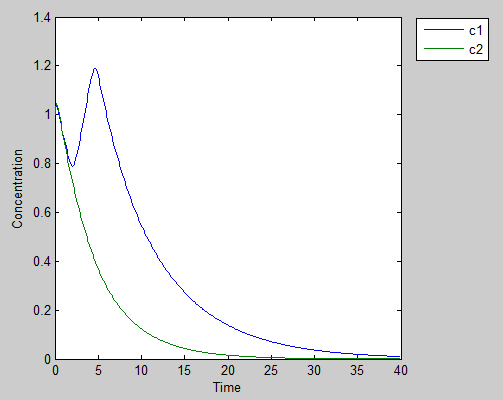
What will happen if we put two people with different sensibility of other’s goodwill into this dilemma? To achieve this, we can simply adjust the Hill coefficient of the differential equation of Zeor, to see what have found.

There appears a clear game between our prisoners, and unlike other results this dynamic equilibrium crashed at last. It’s usually a common sense that the damped oscillation may lead to a stable equilibrium, , but you can hardly tell which people made the mistake. How our prisoners can perform such clumsy play, maybe we can have a further study.

This media liked the whole modeling of our project.

Media:modelingsustc.pdf

@@ Line 8: / Line 8: @@
 !align="center"|[[Team:SUSTC-Shenzhen-A/Modeling|Modeling]]
 !align="center"|[[Team:SUSTC-Shenzhen-A/Notebook|Protocol and notes]]
-!align="center"|[[Team:SUSTC-Shenzhen-A/Safety|Safety]]
+!align="center"|[[Team:SUSTC-Shenzhen-A/Safety|Safety and security]]
 !align="center"|[[Team:SUSTC-Shenzhen-A/Attributions|Attributions]]
 !align="center"|[[Team:SUSTC-Shenzhen-A/Human Practice|Human Practice]]