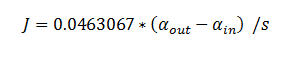Team:SydneyUni Australia/Modelling Results
From 2013.igem.org
| Line 66: | Line 66: | ||
===='''Output:'''==== | ===='''Output:'''==== | ||
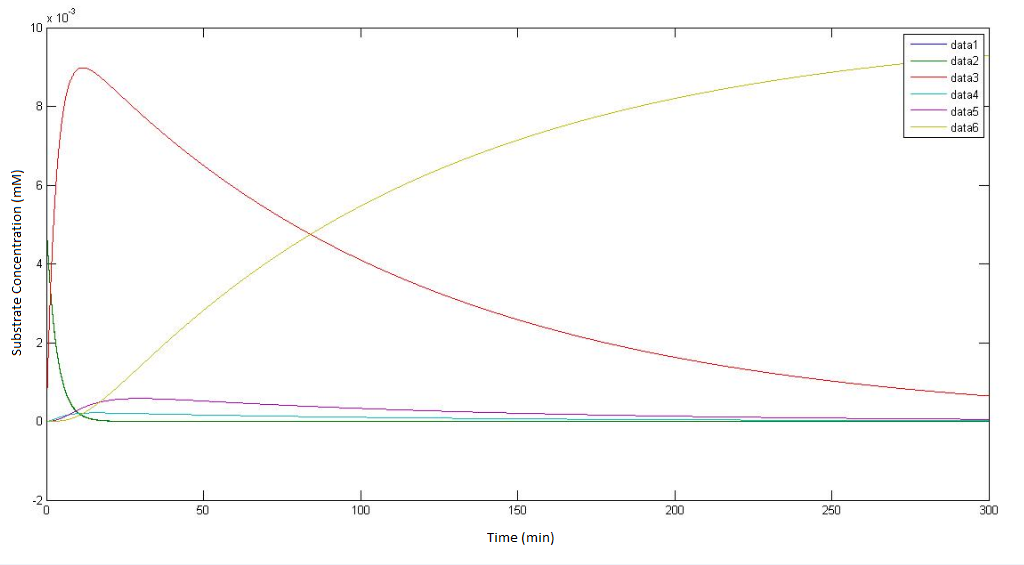
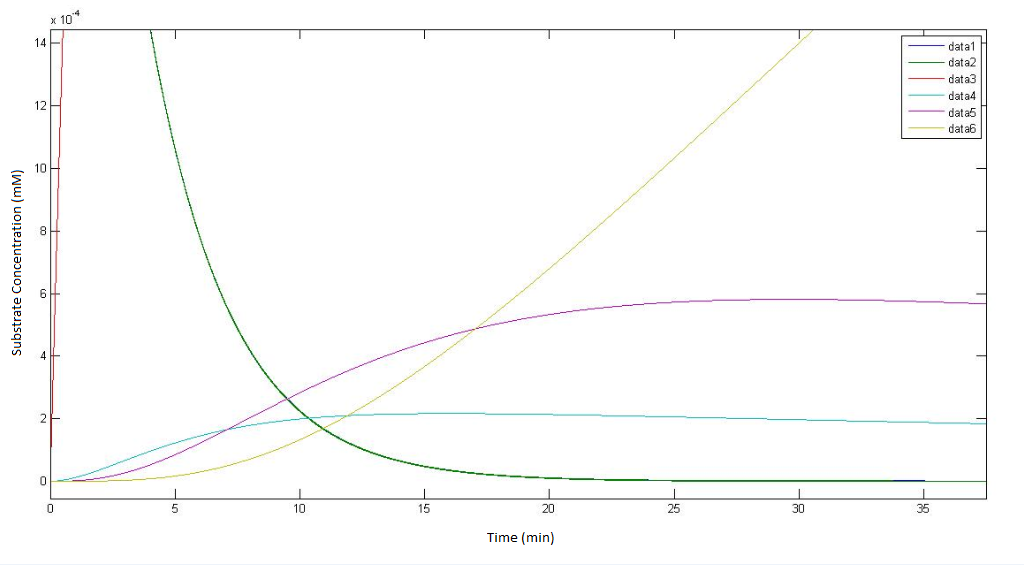
| - | The output of the raw MATLAB code for the pathway not involving p450 which | + | The output of the raw MATLAB code for the pathway not involving p450 which depict how the concentrations of each metabolite change over time. The 't=0 min' time point is the point where the engineered cells are instantaneously introduced (and evenly homogenised) to a solution of DCA with an initial concentratioN OF 0.1Mm. |
| Line 76: | Line 76: | ||
Regarding the figure legends with in the graphs themselves data 1, data 2, data 3, data 4, data 5 * data 6, represents the concentration of the metabolites αin, αout, β, γ, δ & ε respectively. | Regarding the figure legends with in the graphs themselves data 1, data 2, data 3, data 4, data 5 * data 6, represents the concentration of the metabolites αin, αout, β, γ, δ & ε respectively. | ||
| + | The bottom graph is a rescaled version of the top graph so as to achieve a higher resolution the dynamics of the metabolites. | ||
== '''References:''' == | == '''References:''' == | ||
Revision as of 04:14, 28 September 2013


Running the Model
All enzyme concentrations were given a value of 0.1 mM. The temperature was set as T=298K. A plasma membrane distance of d=2nm was given. The cell concentration was given as 1E8 cells/mL. No cellular growth rate was implemented. Glycolate, ε, was left ‘unprocessed’, i.e. it is left to simply accumulate.
Using the constants above the flux took the value:
Assumptions
- All enzymes follow MM kinetics as described in the literature.
- The enzymes and metabolites are homogeneously distributed within the cell.
- The metabolites in the pathway are processed only by the proposed enzymes.
- The enzyme concentrations remain constant.
- The partition coefficient for DCA in octanol and water is approximately the same as the partition coefficient for the cell membrane.
- The cells only grow/divide through DCA-derived-glycolate.
- Diffusion can accurately follow
- All cells are of the same size (ie equal membrane surface area)
Raw MATLAB code:
function dy = nop450(t,y) dy=zeros(6,1); dy(1)= -6*(10^4)*0.0463067*(y(1)-y(2)); dy(2)= 6*(10^4)*0.0463067*(y(1)-y(2))-3.3*0.1*(y(2)/(0.53+y(2))); dy(3)= 3.3*0.1*(y(2)/(0.53+y(2)))-0.0871*0.1*(y(3)/(0.94+y(3))); dy(4)= .0871*0.1*(y(3)/(0.94+y(3)))- 0.6*0.1*(y(4)/(0.16+y(4))); dy(5)= 0.6*0.1*(y(4)/(0.16+y(4))) - 25.4*0.1*(y(5)/(20+y(5))); dy(6)= 25.4*0.1*(y(5)/(20+y(5))); end
Raw MATLAB code for the pathway not involving p450
function dy = p450(t,y) dy=zeros(5,1); dy(1)= -6*(10^12)*0.0463067*(y(1)-y(2)); dy(2)= 6*(10^12)*0.0463067*(y(1)-y(2))-89.8*0.1*(y(2)/(7.2+y(2))); dy(3)= 89.8*0.1*(y(2)/(7.2+y(2)))-0.6*0.1*(y(3)/(0.16+y(3))); dy(4)= 0.6*0.1*(y(3)/(0.16+y(3))) - 25.4*0.1*(y(4)/(20+y(4))); dy(5)= 25.4*0.1*(y(4)/(20+y(4))); end
Raw MATLAB code for the pathway involving p450
Output:
The output of the raw MATLAB code for the pathway not involving p450 which depict how the concentrations of each metabolite change over time. The 't=0 min' time point is the point where the engineered cells are instantaneously introduced (and evenly homogenised) to a solution of DCA with an initial concentratioN OF 0.1Mm.
Regarding the figure legends with in the graphs themselves data 1, data 2, data 3, data 4, data 5 * data 6, represents the concentration of the metabolites αin, αout, β, γ, δ & ε respectively. The bottom graph is a rescaled version of the top graph so as to achieve a higher resolution the dynamics of the metabolites.
References:
[1] Krooshof, G. H., I. S. Ridder, et al. (1998). "Kinetic Analysis and X-ray Structure of Haloalkane Dehalogenase with a Modified Halide-Binding Site†." Biochemistry 37(43): 15013-15023.
[2] Janecki, D. J., K. G. Bemis, et al. (2007). "A multiple reaction monitoring method for absolute quantification of the human liver alcohol dehydrogenase ADH1C1 isoenzyme." Analytical Biochemistry 369(1): 18-26.
[3] Pandey, A. V. and C. E. Flück (2013). "NADPH P450 oxidoreductase: Structure, function, and pathology of diseases." Pharmacology & Therapeutics 138(2): 229-254.
[4] van der Ploeg, J., Shmidt, M. P., Landa, A. S., and Janssen, D. B. (1994). "Identification of Chloroacetaldehyde Dehydrogenase Involved in 1,2-Dichloroethane Degradation." Applied Environmental Microbiology (60(5): 1699-1605.
[5] van der Ploeg, J., van Hall, G., Janssen, D. B. (1991) "Characterization of the haloacid dehalogenase from Xanthobacter autotrophicus GJ10 and sequencing of the dhlB gene." Journal of Bacteriology 173(24):7925-33.
[6] Sinensky, Mi “Homeoviscous Adaption – A Homeostatic Process that Regulates the Viscosity of Membrane Lipids in Escheria coli” Proceedings from the National Academy of Science 71(2): 522-525.
[7] CyberCell Database
 "
"