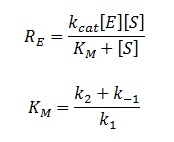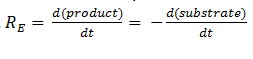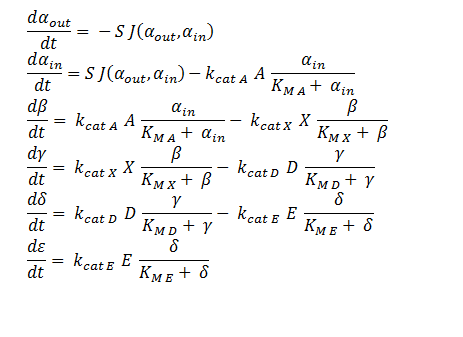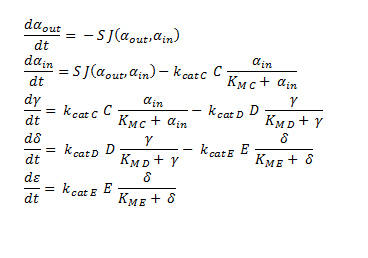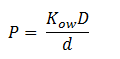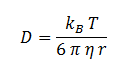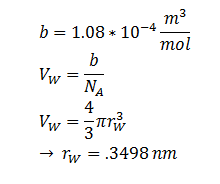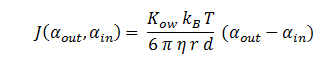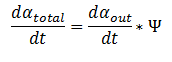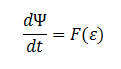Team:SydneyUni Australia/Modelling Principles
From 2013.igem.org
Jbergfield (Talk | contribs) |
|||
| Line 7: | Line 7: | ||
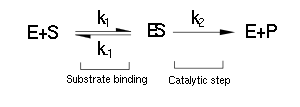
| - | <div align="justify">The majority of single-substrate metabolic enzymes follow MM kinetics, for which the equations accurately describe enzyme activity. The system is based on the forward and reverse kinetic rate (k<sub>1</sub> and k<sub>-1</sub> respectively) of substrate-enzyme binding followed by the irreversible catalytic step of product formation (k<sub>2</sub>) as depicted in the figure below: | + | <div align="justify">The majority of single-substrate metabolic enzymes follow Michaelis-Menton (MM) kinetics, for which the equations below accurately describe enzyme activity. The system is based on the forward and reverse kinetic rate (k<sub>1</sub> and k<sub>-1</sub> respectively) of substrate-enzyme binding followed by the irreversible catalytic step of product formation (k<sub>2</sub>) as depicted in the figure below: |
</div> | </div> | ||
| Line 16: | Line 16: | ||
<div align="justify"> | <div align="justify"> | ||
| - | The rate of catalysis for an enzyme is a function of the enzyme and substrate concentration and incorporates the catalytic constant K<sub>cat</sub> and the Michaelis constant K<sub>m</sub>, which are given in most of the literature that involves enzyme kinetics. The symbol | + | The rate of catalysis for an enzyme is a function of the enzyme and substrate concentration and incorporates the catalytic constant K<sub>cat</sub> and the Michaelis constant K<sub>m</sub>, which are given in most of the literature that involves enzyme kinetics. The symbol R<sub>E</sub> denotes the reaction rate: the rate of product formation, i.e. </div> |
[[File:Igem Re= dproduct.png|center]] | [[File:Igem Re= dproduct.png|center]] | ||
| Line 27: | Line 27: | ||
<div align="justify"> | <div align="justify"> | ||
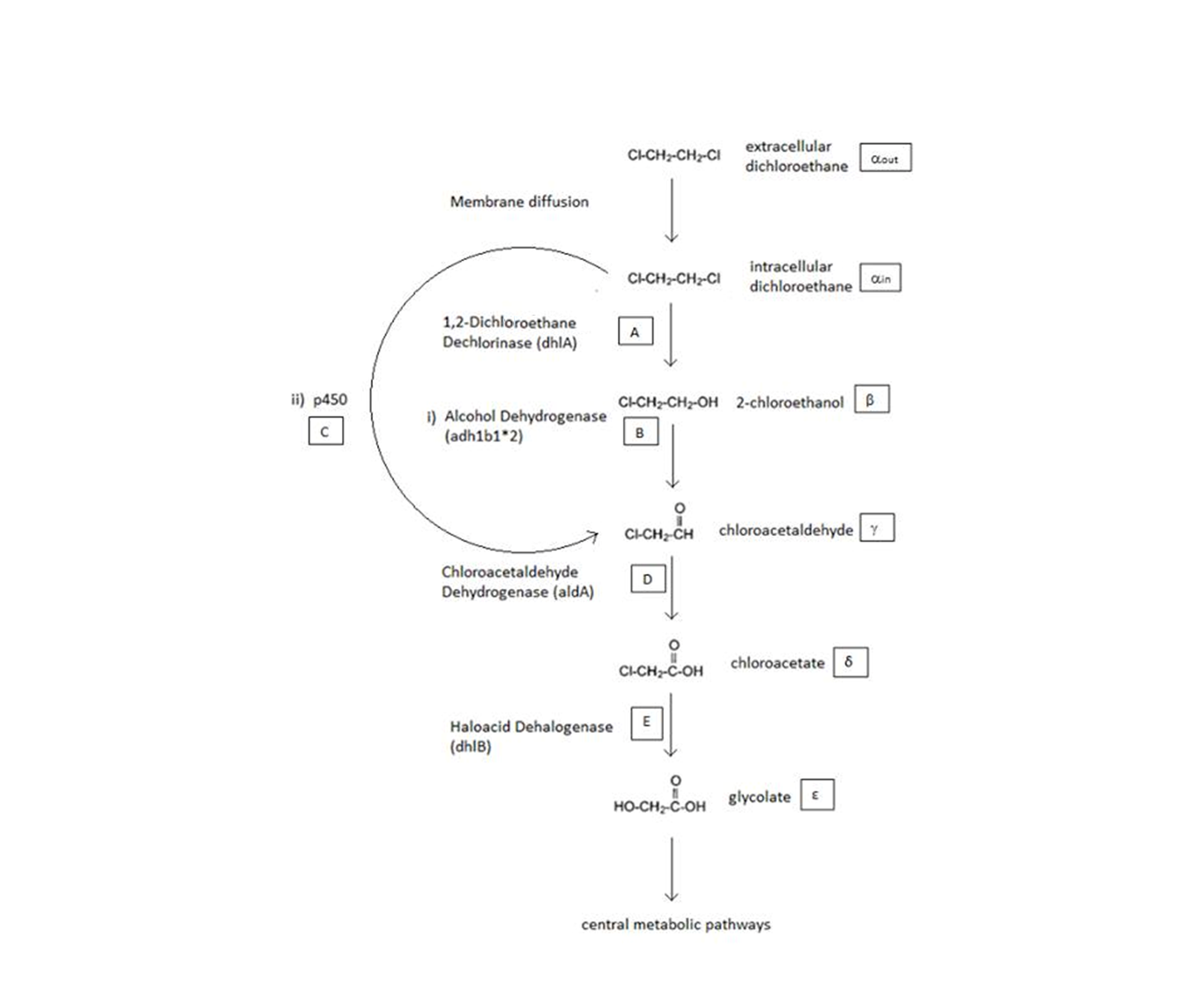
| - | In the above figure is a simplified schematic of the 2 metabolic pathways | + | In the above figure is a simplified schematic of the 2 metabolic pathways we considered. The symbols in squares signify the intracellular concentrations of the associated metabolite (Greek letters) or enzyme (capital English letters). </div> |
| Line 37: | Line 37: | ||
!Enzyme !! Gene !! Symbol !! Constants !! Substrate !! Product !! Ref | !Enzyme !! Gene !! Symbol !! Constants !! Substrate !! Product !! Ref | ||
|- | |- | ||
| - | |1,2-Dichloroethane Dechlorinase || dhlA || A || K<sub>M A</sub>=0. 53 mM, k<sub>cat A</sub> = 3.3 s<sup>-1</sup> || DCA || 2-chloroethanol || [1] | + | |1,2-Dichloroethane Dechlorinase || dhlA || A || K<sub>M A</sub> = 0.53 mM, k<sub>cat A</sub> = 3.3 s<sup>-1</sup> || DCA || 2-chloroethanol || [1] |
|- | |- | ||
| - | |Alcohol Dehydrogenase || Adhlb 1/2* || B || K<sub>M B</sub>=0. 94 mM, k<sub>cat B</sub> = 0.0871 s<sup>-1</sup> || 2-chloroethanol || chloroacetaldehyde || [2] | + | |Alcohol Dehydrogenase || Adhlb 1/2* || B || K<sub>M B</sub> = 0.94 mM, k<sub>cat B</sub> = 0.0871 s<sup>-1</sup> || 2-chloroethanol || chloroacetaldehyde || [2] |
|- | |- | ||
|p450 || p450 || C || K<sub>M C</sub> = 7.2 mM, k<sub>cat C</sub> = 89.8 s<sup>-1</sup> || DCA || chloroacetaldehyde || [3] | |p450 || p450 || C || K<sub>M C</sub> = 7.2 mM, k<sub>cat C</sub> = 89.8 s<sup>-1</sup> || DCA || chloroacetaldehyde || [3] | ||
| Line 45: | Line 45: | ||
|Chloroacetaldehyde Dehydrogenase || aldA || D || K<sub>M D</sub> = 0.06mM, k<sub>cat D</sub> = 0.60 s<sup>-1</sup> || chloroacetaldehyde || chloroacetate || [4] | |Chloroacetaldehyde Dehydrogenase || aldA || D || K<sub>M D</sub> = 0.06mM, k<sub>cat D</sub> = 0.60 s<sup>-1</sup> || chloroacetaldehyde || chloroacetate || [4] | ||
|- | |- | ||
| - | |Haloacetate Dehydrogenase || dhlB || E || K<sub>M E</sub>= 20 mM, k<sub>cat E</sub> = 25.4 s<sup>-1</sup> || chloroacetate || glycolate || [5] | + | |Haloacetate Dehydrogenase || dhlB || E || K<sub>M E</sub> = 20 mM, k<sub>cat E</sub> = 25.4 s<sup>-1</sup> || chloroacetate || glycolate || [5] |
|} | |} | ||
</center> | </center> | ||
| Line 55: | Line 55: | ||
[[File:Igem ode 1.png|center]] | [[File:Igem ode 1.png|center]] | ||
| - | + | ODEs describing the pathway not involving p450 | |
[[File:Igem ode 2.png|center]] | [[File:Igem ode 2.png|center]] | ||
| - | + | ODEs describing the pathway involving p450 | |
<div align="justify">System of ODEs used to model the intracellular concentration of the metabolic intermediates inside a single cell. The concentrations of each metabolite are determined through the associated MM equation of the introduced enzymes. | <div align="justify">System of ODEs used to model the intracellular concentration of the metabolic intermediates inside a single cell. The concentrations of each metabolite are determined through the associated MM equation of the introduced enzymes. | ||
The symbols A, B, C, D & E represent the intracellular enzyme concentrations the symbols α<sub>in</sub>,α<sub>out</sub>, β, γ & δ represent the concentrations of the metabolic intermediates. | The symbols A, B, C, D & E represent the intracellular enzyme concentrations the symbols α<sub>in</sub>,α<sub>out</sub>, β, γ & δ represent the concentrations of the metabolic intermediates. | ||
| - | The function J(α<sub>out</sub>,α<sub>in</sub> ) represents the flux of extracellular DCA across the plasma membrane and is a function of the extra and intracellular concentrations of DCA. The value S represents the average surface area of the cellular membrane of ''E. coli''. See below for the derivation of J. | + | The function J(α<sub>out</sub>,α<sub>in</sub>) represents the flux of extracellular DCA across the plasma membrane and is a function of the extra and intracellular concentrations of DCA. The value S represents the average surface area of the cellular membrane of ''E. coli''. See below for the derivation of J. |
| - | The initial conditions for the system are | + | The initial conditions for the system are α<sub>in</sub>=β=γ=δ=0 M at t=0 min, ε=ε<sub>phys</sub> & α<sub>out</sub>=α<sub>out</sub>(t=0), where ε is the physiological concentration of non-DCA-derived glycolate and α<sub>out</sub>(t=0) is the initial concentration of DCA outside of the cellular membrane. |
| - | + | </div> | |
| Line 81: | Line 81: | ||
[[File:p=kow.png|center]] | [[File:p=kow.png|center]] | ||
| - | <div align="justify">Where D is the diffusion constant of DCA across the plasma membrane and d is the length of the membrane. The partition coefficient for DCA across a plasma membrane is not documented, but can be estimated to the octanal-water partition coefficient (K<sub>ow</sub>). This constant | + | <div align="justify">Where D is the diffusion constant of DCA across the plasma membrane and d is the length of the membrane. The partition coefficient for DCA across a plasma membrane is not documented, but can be estimated to the octanal-water partition coefficient (K<sub>ow</sub>). This constant is the equilibrium ratio of DCA in octanol and water. |
The diffusion constant, D, is not documented in the literature but can be estimated through the Stokes-Einstein equation based on an estimation of the radius of DCA and viscosity of the cellular membrane.</div> | The diffusion constant, D, is not documented in the literature but can be estimated through the Stokes-Einstein equation based on an estimation of the radius of DCA and viscosity of the cellular membrane.</div> | ||
| Line 107: | Line 107: | ||
|η || Cellular Membrane Viscosity || 1.9 kg/m/s || [6] | |η || Cellular Membrane Viscosity || 1.9 kg/m/s || [6] | ||
|- | |- | ||
| - | |S || E. coli Membrane Surface Area || | + | |S || E. coli Membrane Surface Area || 6x10<sup>-12</sup> m<sup>2</sup> || [7] |
|- | |- | ||
|r || DCA radius || 0.3498 nm || [8] | |r || DCA radius || 0.3498 nm || [8] | ||
| Line 119: | Line 119: | ||
=='''Extending the System to Cell Cultures'''== | =='''Extending the System to Cell Cultures'''== | ||
| - | <div align="justify">The model can be extended to a homogeneous solution/culture of cells. Let Ψ represent the concentration of the cells in solution. The overall rate of decrease of DCA ( | + | <div align="justify">The model can be extended to a homogeneous solution/culture of cells. Let Ψ represent the concentration of the cells in solution. The overall rate of decrease of DCA (α<sub>total</sub>) in solution is |
</div> | </div> | ||
Revision as of 03:28, 18 October 2013


A Brief Background on Michaelis-Menton Kinetics
A Schematic of the Engineered Metabolic Pathway:
General Information regarding the Enzymes Involved in the Metabolic Pathway
| Enzyme | Gene | Symbol | Constants | Substrate | Product | Ref |
|---|---|---|---|---|---|---|
| 1,2-Dichloroethane Dechlorinase | dhlA | A | KM A = 0.53 mM, kcat A = 3.3 s-1 | DCA | 2-chloroethanol | [1] |
| Alcohol Dehydrogenase | Adhlb 1/2* | B | KM B = 0.94 mM, kcat B = 0.0871 s-1 | 2-chloroethanol | chloroacetaldehyde | [2] |
| p450 | p450 | C | KM C = 7.2 mM, kcat C = 89.8 s-1 | DCA | chloroacetaldehyde | [3] |
| Chloroacetaldehyde Dehydrogenase | aldA | D | KM D = 0.06mM, kcat D = 0.60 s-1 | chloroacetaldehyde | chloroacetate | [4] |
| Haloacetate Dehydrogenase | dhlB | E | KM E = 20 mM, kcat E = 25.4 s-1 | chloroacetate | glycolate | [5] |
* values based on ethanol as a substrate
ODE Model
ODEs describing the pathway not involving p450
ODEs describing the pathway involving p450
The symbols A, B, C, D & E represent the intracellular enzyme concentrations the symbols αin,αout, β, γ & δ represent the concentrations of the metabolic intermediates. The function J(αout,αin) represents the flux of extracellular DCA across the plasma membrane and is a function of the extra and intracellular concentrations of DCA. The value S represents the average surface area of the cellular membrane of E. coli. See below for the derivation of J. The initial conditions for the system are αin=β=γ=δ=0 M at t=0 min, ε=εphys & αout=αout(t=0), where ε is the physiological concentration of non-DCA-derived glycolate and αout(t=0) is the initial concentration of DCA outside of the cellular membrane.
DCA Diffusion Across the Plasma Membrane
The diffusion of DCA across the cell membrane was modelled based on Fick’s first law of diffusion:
In Summary, the flux across the membrane is:
| Symbol | Name | Value (units) | Ref |
|---|---|---|---|
| η | Cellular Membrane Viscosity | 1.9 kg/m/s | [6] |
| S | E. coli Membrane Surface Area | 6x10-12 m2 | [7] |
| r | DCA radius | 0.3498 nm | [8] |
| Kow | Octanol-water Partition Coefficient for DCA | 28.2 | [9] |
| d | Length of Cellular Membrane | ??? | [10] |
Extending the System to Cell Cultures
By applying this change, the resulting values of αin,αout, β, γ & δ represent the metabolite concentration across all cells.
Furthermore the cells are expected to grow due to the production of glycolate (which can be used as a carbon source for growth).
 "
"