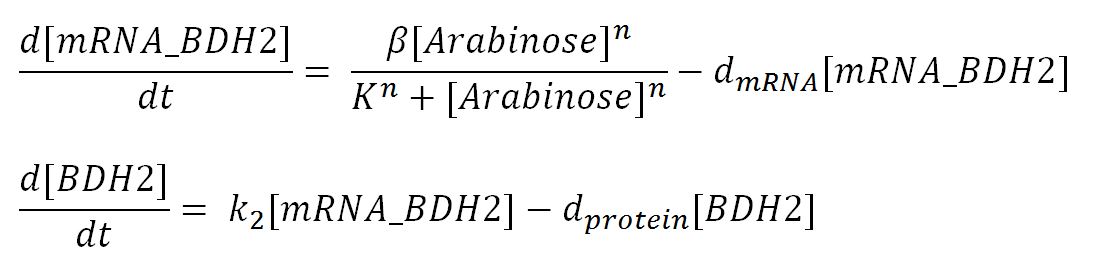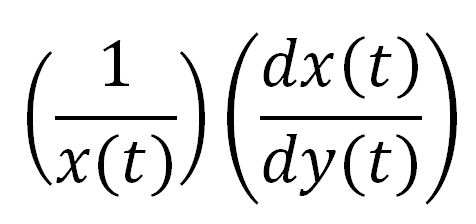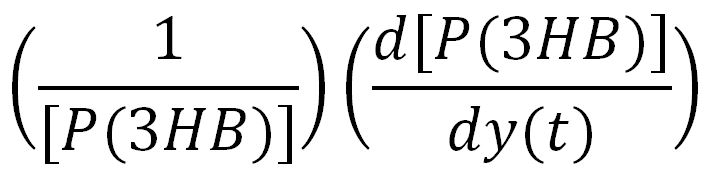(Difference between revisions)

Contents 1 Modelling: P(3HB) synthesis module 1.1 Specifications 1.2 Deterministic model 1.3 ODEs in Matlab Simbiology model 1.3.1 Genetic regulations and expressions 1.3.1.1 BDH2 (3-hydroxybutyrate dehydrogenase) 1.3.1.2 PhaB (Acetoacetyl-CoA reductase)and PhaC (P(3HB) synthase) 1.3.1.3 Values, sources and assumptions 1.3.2 Enzyme kinetics 1.3.2.1 BDH2 (3-hydroxybutyrate dehydrogenase) 1.3.2.2 atoAD (Acetyl-CoA:acetoacetyl-CoA transferase (α and β subunits)) 1.3.2.3 phaB (Acetoacetyl-CoA reductase) 1.3.2.4 phaC (P(3HB) synthase) 1.4 Simulation results 1.4.1 P(3HB) production 1.5 Model-guided design and optimisation 1.5.1 Sensitivity analysis: species concentrations 1.5.2 Scan with different levels of PhaB 1.5.3 Difference between promoter expressions after optimisation 1.6 Metabolic considerations 1.6.1 Effect on growth and interference with metabolism 1.6.2 Initial concentrations of metabolites 1.7 References

Modelling: P(3HB) synthesis module

This page is about modelling the plastic-synthesising module developed in our project. The plastic that this module synthesises is the bioplastic poly-3-hydroxybutyrate, also known as P(3HB). The content below shows the process of building, designing and optimisation of the model. Also, the considerations, assumptions and limitations will be discussed.

Specifications

• Input = monomer (3HB)
• Output = polymer (P(3HB))

Deterministic model

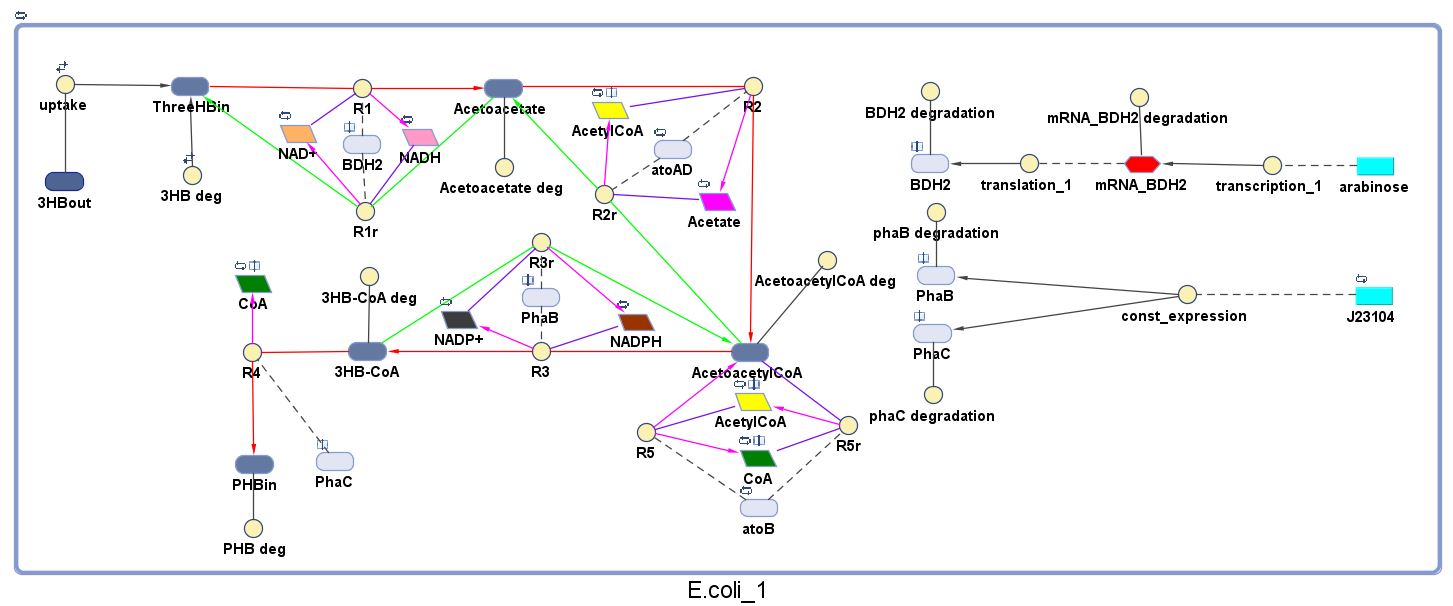
The model was built and simulated in Simbiology, a Matlab package designed for modelling biological systems. In our model we have a compartment (labelled "E. coli_1") that represents our engineered cell. The compartment contains the reactions and species that interact with the polymer synthesis pathway.

The pathways on the right half of the cell are genetic expressions of the 3 enzymes involved in the plastic synthesis pathway. The pathways on the left represent the actual P(3HB) production pathway.

ODEs in Matlab Simbiology model

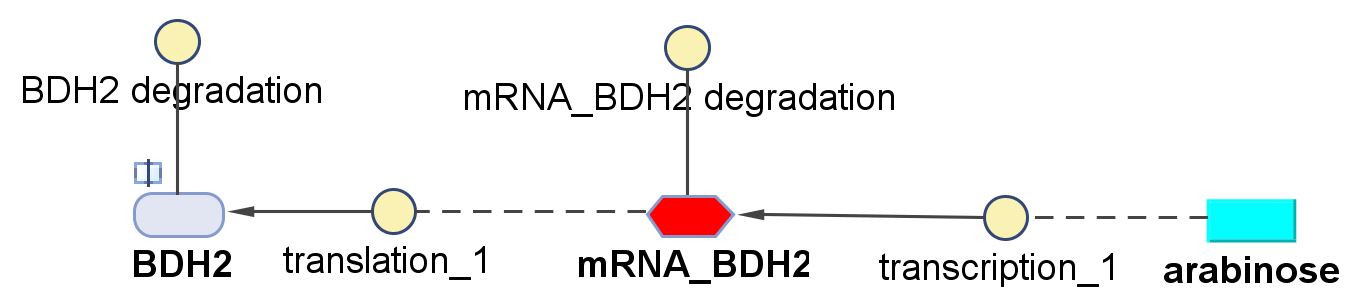
Genetic regulations and expressions

BDH2 (3-hydroxybutyrate dehydrogenase)

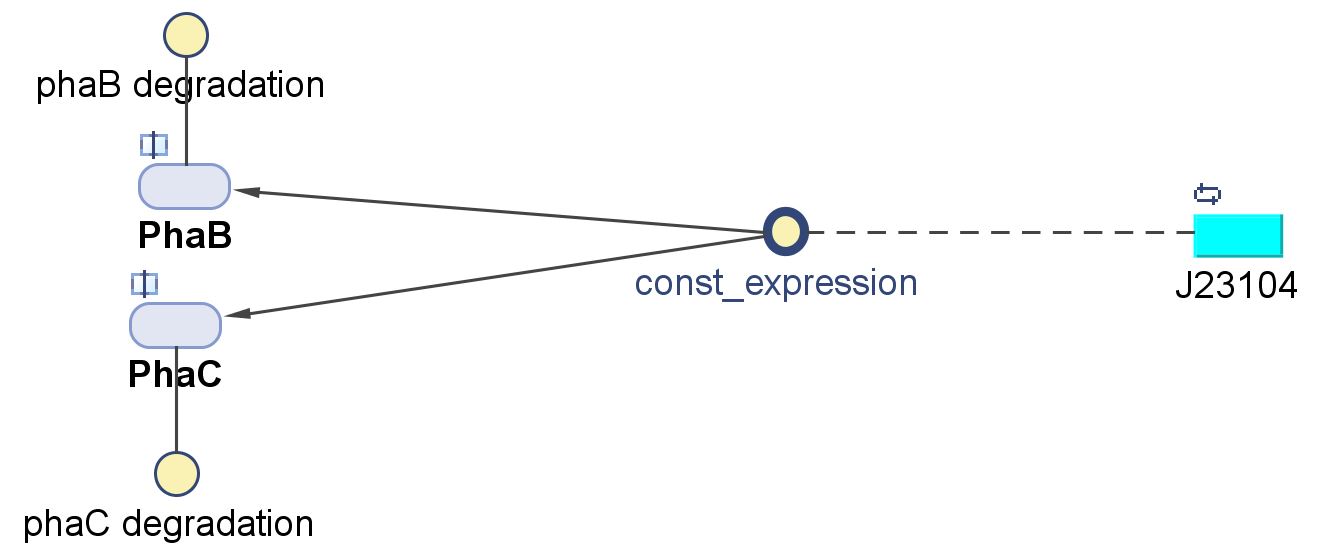
PhaB (Acetoacetyl-CoA reductase)and PhaC (P(3HB) synthase)

Values, sources and assumptions

Parameter	Description	Value	Units	Sources	Assumptions
β	maximum rate of transcription	0.032	mM/min	Please see derivation below	Please see derivation below
n	Hill coefficient	2.0	dimensionless
K	Activation coefficient	0.0031	mM
d_mRNA	mRNA degradation rate	0.1	1/min
d_protein	Protein degradation rate	0.050	1/min		There is no active degradation pathway and that dilution is the dominant way by which the protein level decreases in a cell
k2	mRNA production rate	4.7	1/min
k3	Protein production rate	0.039	1/min
[Arabinose]	Concentration of arabinose	Initial: 0.008	mM
[mRNA]	Concentration of mRNA	-	mM	-	-
[BDH2]	Concentration of BDH2	-	mM	-	-
[PhaB]	Concentration of PhaB	-	mM	-	-
[PhaC]	Concentration of PhaB	-	mM	-	-

Derivation of the maximal expression rate,β

Enzyme kinetics

BDH2 (3-hydroxybutyrate dehydrogenase)

atoAD (Acetyl-CoA:acetoacetyl-CoA transferase (α and β subunits))

phaB (Acetoacetyl-CoA reductase)

phaC (P(3HB) synthase)

Simulation results

P(3HB) production

Model-guided design and optimisation

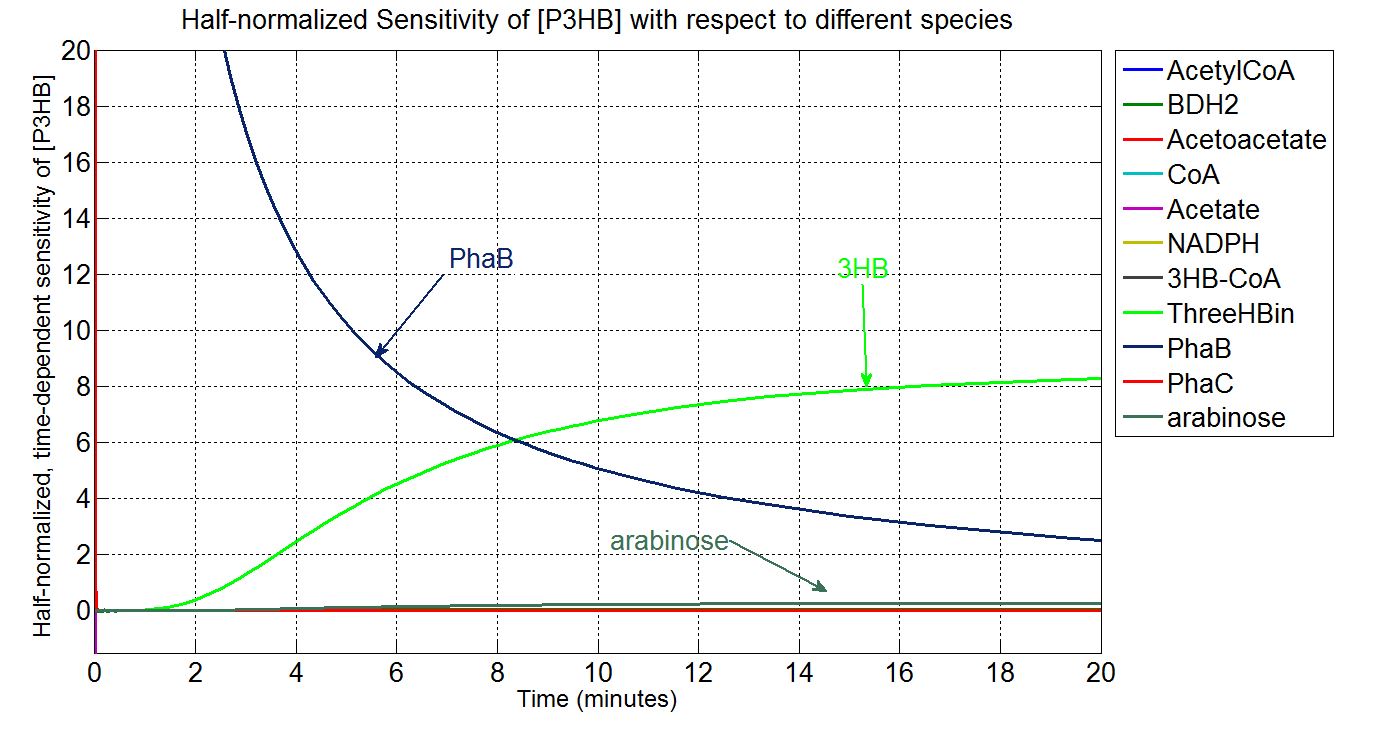
Sensitivity analysis: species concentrations

What is sensitivity analysis and why do it?

In order to look at how we could increase the production of P(3HB) we decided to run a sensitivity analysis (also in Simbiology) to identify what species in the model P(3HB) is sensitive to, given the specific conditions with which we set the model. In other words, we calculated the time-dependent sensitivity of P(3HB) with respect to the initial conditions of other species (species formed along the synthesis pathway and enzymes involved).[http://www.mathworks.co.uk/help/simbio/ug/calculating-sensitivities.html#brbumlr|ref]

For a species x, whose concentration depends on time, it can be expressed as x(t). To calculate the sensitivity of x(t) with respect to another species y(t), the sensitivity with normalisation relative to the numerator x(t) can be calculated as:

Therefore, the underlying algorithm for this sensitivity analysis of P(3HB) is:

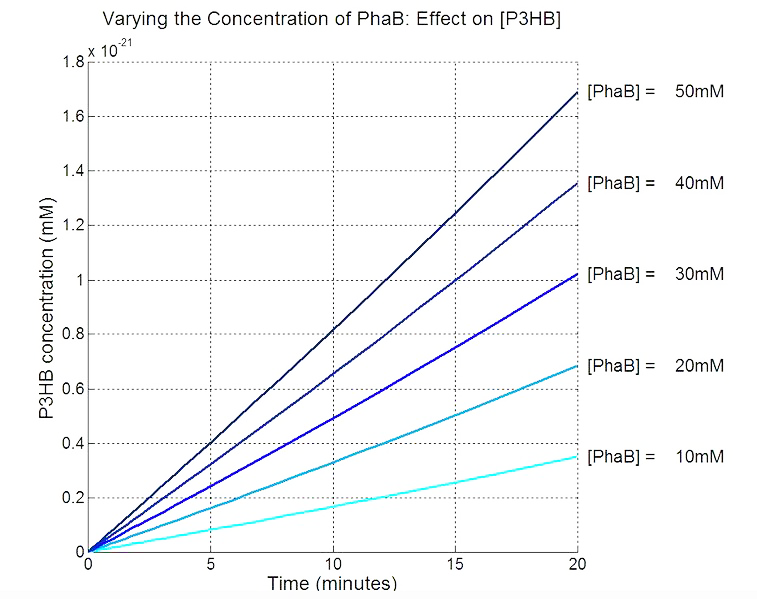
Scan with different levels of PhaB

The plot below is to show that increasing PhaB concentration within the engineered organism would have a positive effect on the concentration of the P(3HB) synthesised. As so many parameters within the model were taken from different sources, it would be difficult to give a simulation plot that is accurate quantitatively. It was decided to show the single cell simulation for this because the scans were carried out up to the doubling time of 20mins, hence avoided the issue of scaling-up which would have otherwise subjected the simulation to more errors. Therefore, this plot should be interpreted from a qualitative perspective and the trend should be observed.

Difference between promoter expressions after optimisation

Metabolic considerations

The metabolic model predicts the interaction of our pathway with endogenous pathways. In synthetic biology, an ideal system is fully orthogonal. However, it can be the case, such as here that coenzymes are needed for the reaction steps in a metabolic pathway. When we realised that our pathway uses a lot of Co-A, we constructed a model to see how this can be recycled and predict whether it would negatively effect the chassis. Tell that the Co-A is regenerated at the same speed as it is used and therefore there is not a huge amount of Co-A "stuck" in the pathway at any one time. (Bobby, how much Co-A is that exactly?) This informed us about that the cells should be able to bear the burden of the pathway.

Metabolic model to optimise PHB production. Tell us how you predicted that phaB is the key enzyme and justify why the increase in enzyme level will increase the amount of PHB. This informed our design and we are changing the promoter in front of the phaCAB operon. Tell that if we can predict that it would be useful to downregulate any genes in the native metabolism of E.coli.

Effect on growth and interference with metabolism

Initial concentrations of metabolites

References