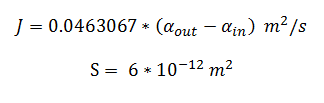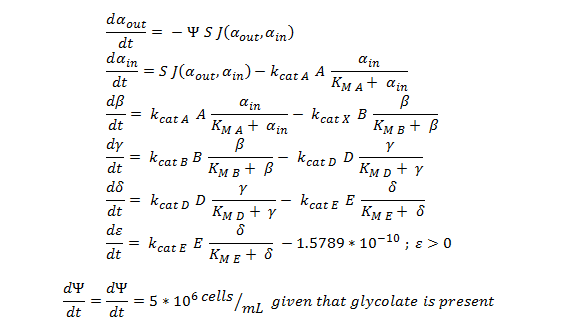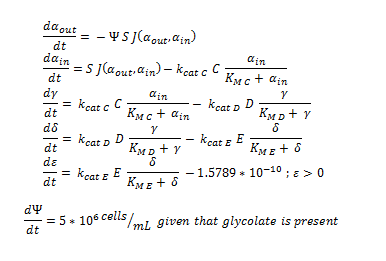Team:SydneyUni Australia/Modelling Results
From 2013.igem.org
| Line 284: | Line 284: | ||
[7] CyberCell Database | [7] CyberCell Database | ||
| + | |||
| + | [8] | ||
| + | |||
| + | [9] | ||
| + | |||
| + | [10] http://www.dtsc.ca.gov/AssessingRisk/Upload/12dca.pdf | ||
| + | |||
| + | [11] | ||
| + | |||
| + | [12] | ||
{{Team:SydneyUni_Australia/Footer}} | {{Team:SydneyUni_Australia/Footer}} | ||
Revision as of 12:11, 25 October 2013


Running the Model
The model was run using MATLAB’s ODE45.
The modelling for both the pathays had initial conditions of:
| Constant | Value | Comment |
|---|---|---|
| KM A | 0.530 mM | From literature [1] |
| kcat A | 3.3 s-1 | From literature [1] |
| KM B | 0.940 mM | From literature [2] |
| kcat B | 0.0871 s-1 | From literature [2] |
| KM C | 7.2 mM | From literature [3] |
| kcat c | 89.8 s-1 | From literature [3] |
| KM D | 0.160 mM | From literature [4] |
| kcat D | 0.600 s-1 | From literature [4] |
| KM E | 20 mM | From literature [5] |
| kcat E | 25.4 s-1 | From literature [5] |
| β, γ, δ & ε | 0 mM | Not naturally present in cells. |
| αout | 1 mM | Initial concentration of DCA in solution (arbitrary) |
| αin | 0.001 mM | Initial concentration of DCA in cell |
| A, B, C, D, E | 25.55 mM | Estimation from literature [], as described in "principles". |
| 2 x 108 cells / mL | Initial cell concentration which allows appropriate growth |
By using the constants summarised in the previous section the flux, J, took the value:
The Non-monooxygenase Pathway
ODE overview:
The summary of the ODE (explained and justified in the previous section).
Raw MATLAB code:
function dy = nop450(t,y)
dy=zeros(7,1);
dy(1)= -y(7)*(6*10^(-12))*0.0463067*(y(1)-y(2));
dy(2)= ((6*10^(-12))*0.0463067*(y(1)-y(2)))-3.3*25.55*(y(2)/(0.53+y(2)));
dy(3)= 3.3*25.55*(y(2)/(0.53+y(2)))-0.0871*25.55*(y(3)/(0.94+y(3)));
dy(4)= .0871*25.55*(y(3)/(0.94+y(3)))- 0.6*25.55*(y(4)/(0.16+y(4)));
dy(5)= 0.6*25.55*(y(4)/(0.16+y(4))) - 25.4*25.55*(y(5)/(20+y(5)));
if y(6) > 2*10^(-10)
dy(6)= 25.4*25.55*(y(5)/(20+y(5))) -1.5789*10^(-10)
else
dy(6) = 25.4*25.55*(y(5)/(20+y(5)))
end
if y(6) > 0.0005
if y(7) > 1.6*10^11
dy(7)=0
else
dy(7) = 5*10^6
end
else
dy(7) = 0
end
end
MATLAB output:
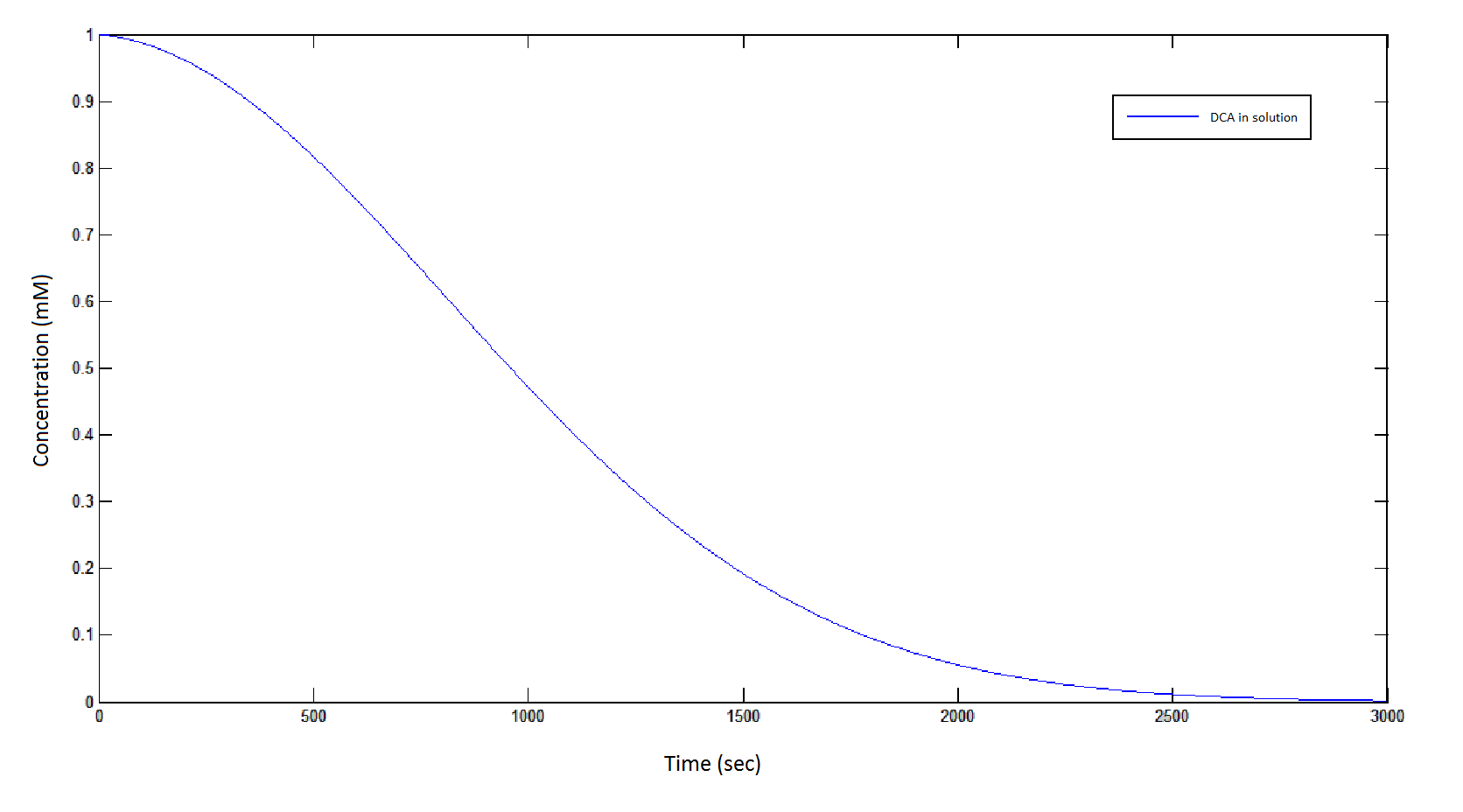
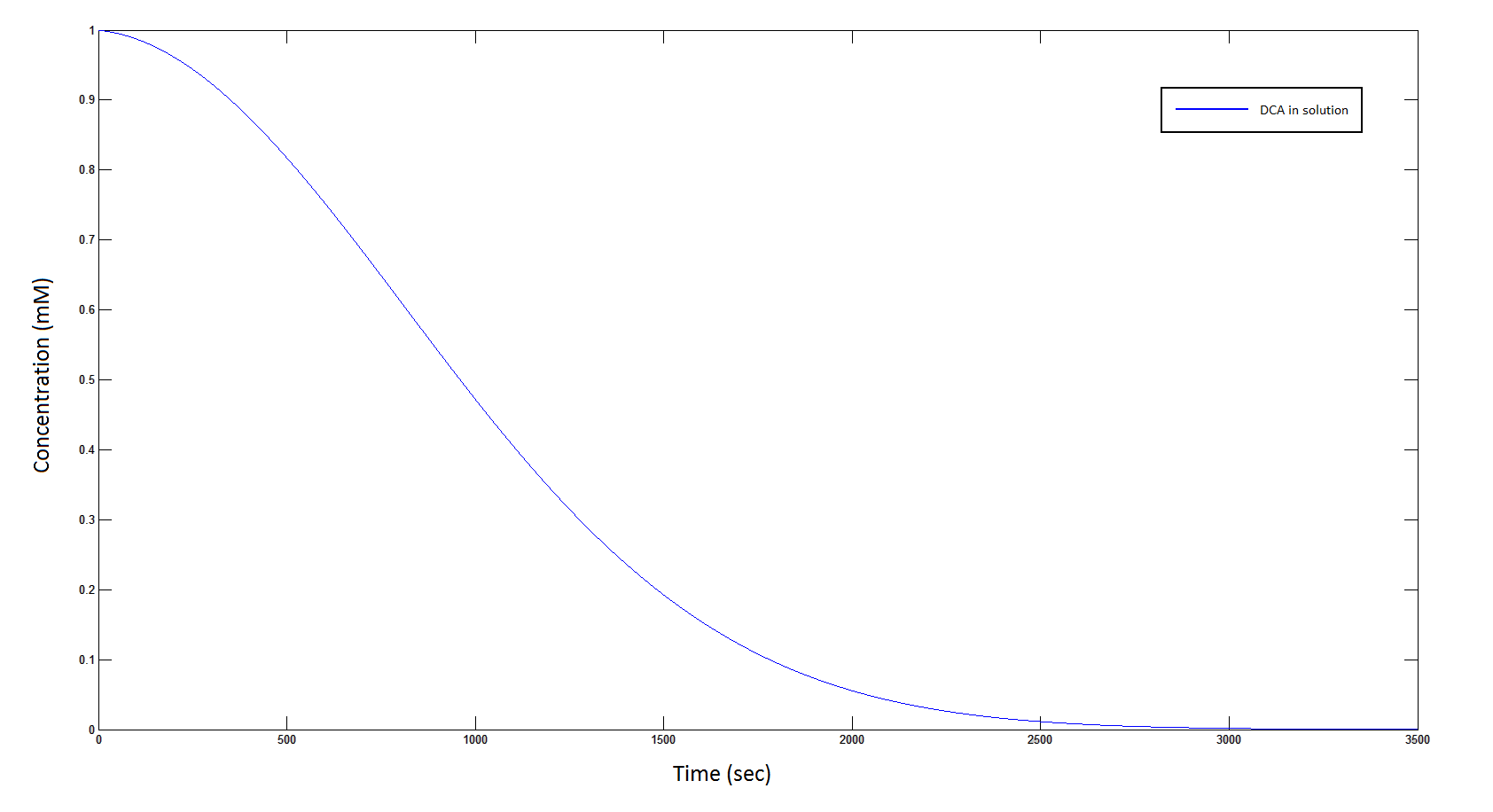
The rate at which DCA is removed in solution:
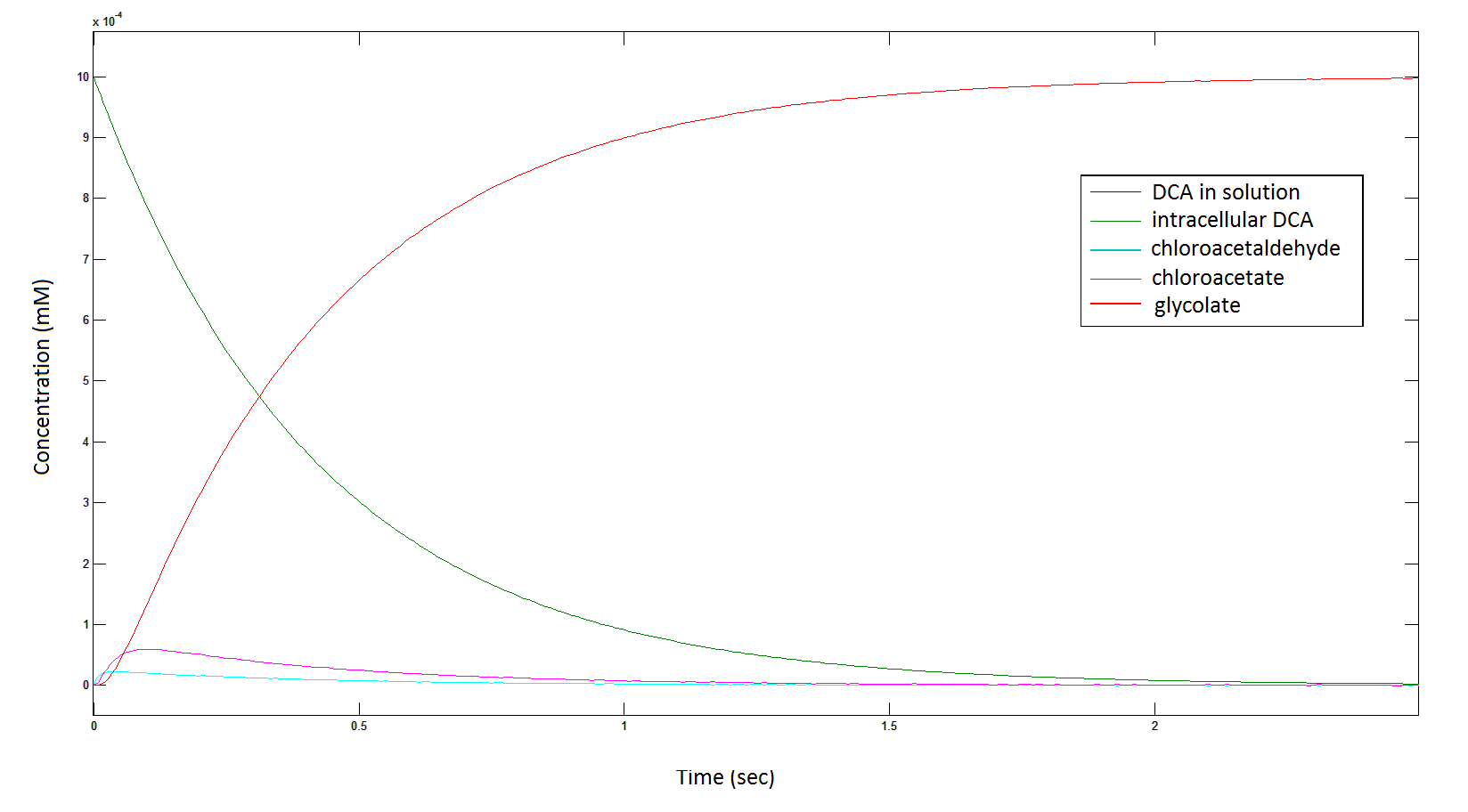
Graph 1: The blue line represents how the concentration of DCA in solution decreases due to the action of our DCA degraders. The red line represents the intracellular concentions of the metabolites (disregard in this graph). One can see that an initial concentration of 2E8 cells/mL completely removes the DCA with a concentration 1mM in (roughly) 150mins.
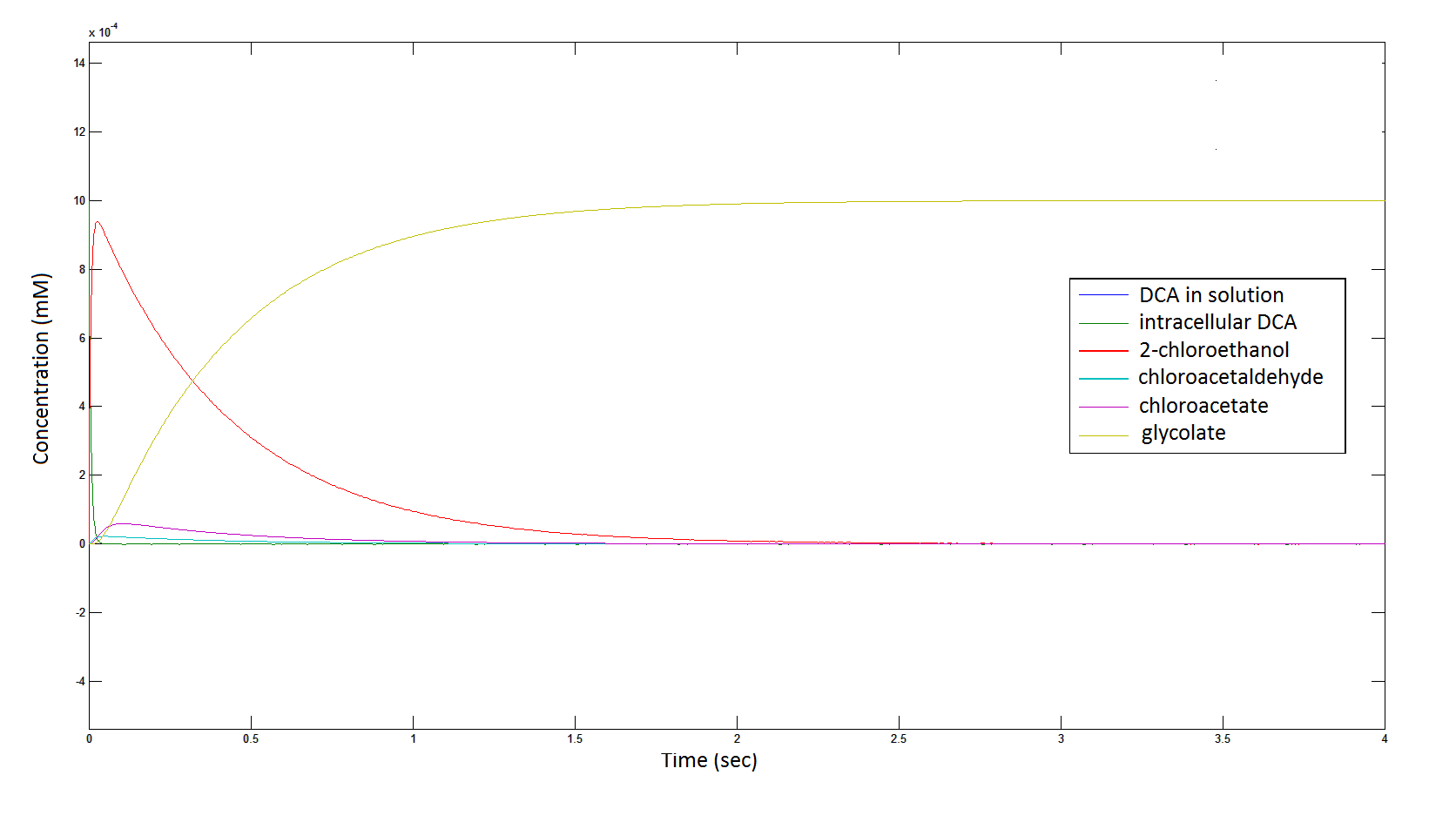
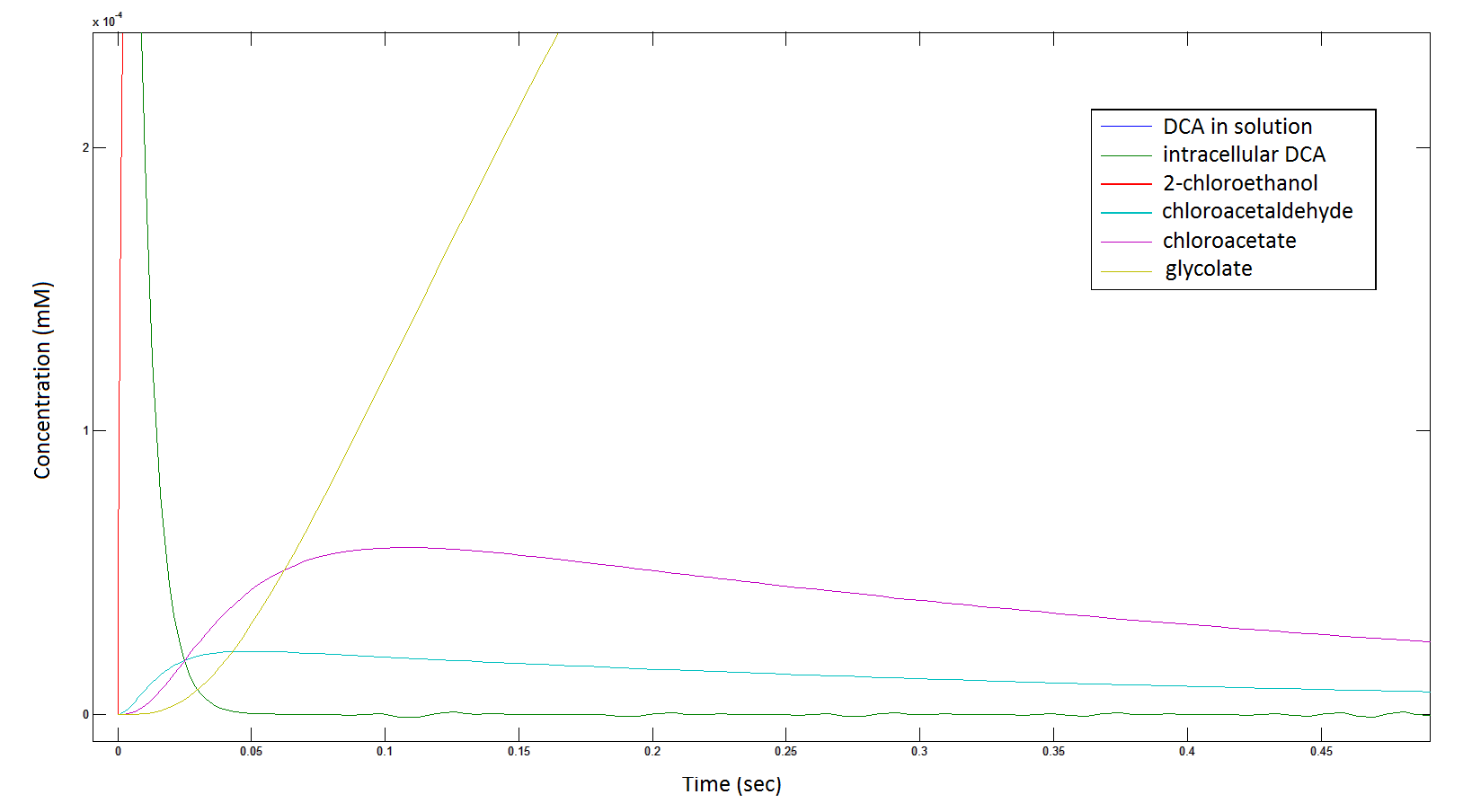
The Rate at which the intracellular concentration of the metabolites change over time:
Graph 2: Each line represents the concentration of each of the metabolites . This graph is simply a rescaling of graph 1. Note: the glycolate won’t accumulate in the cell – it is metabolised – the model had glycolate as the final product. It is used to show that the presence of glycolate can attribute to cell growth.
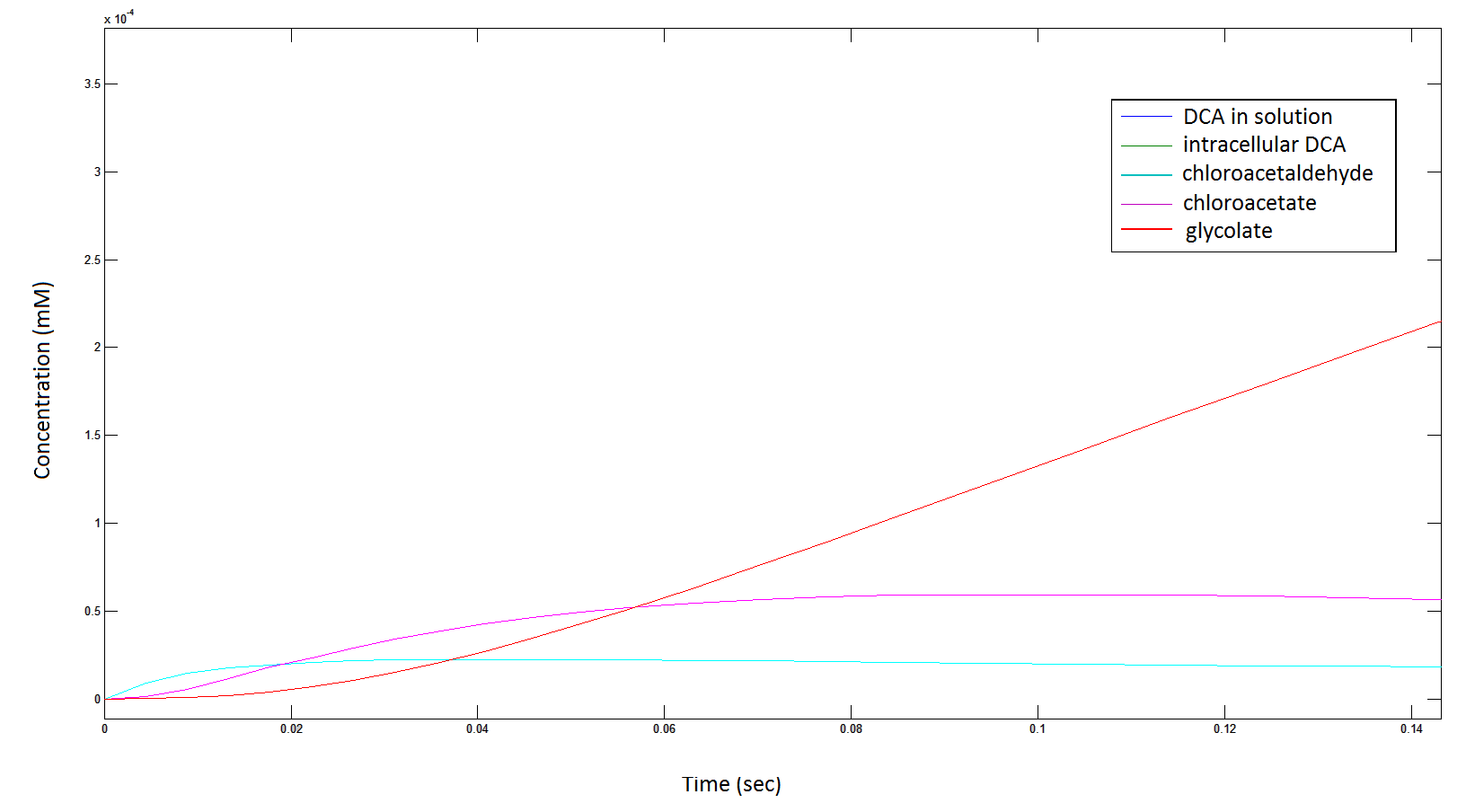
Rescaling the graph once again: the rate at which the metabolic intermediate change over time.
Graph 3: Each line represents the concentration of each of the metabolites . This graph is simply a rescaling of graph 1 and 2.
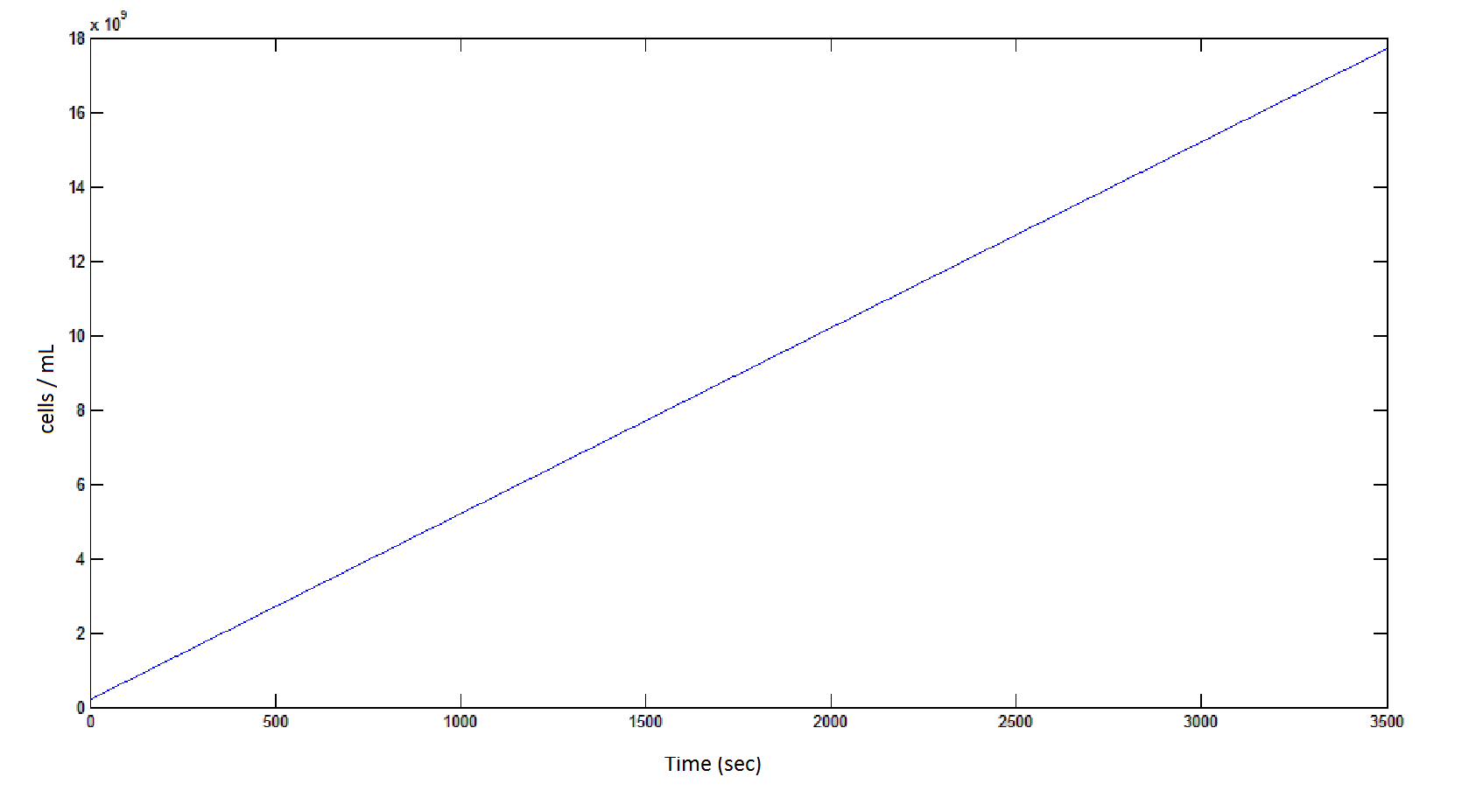
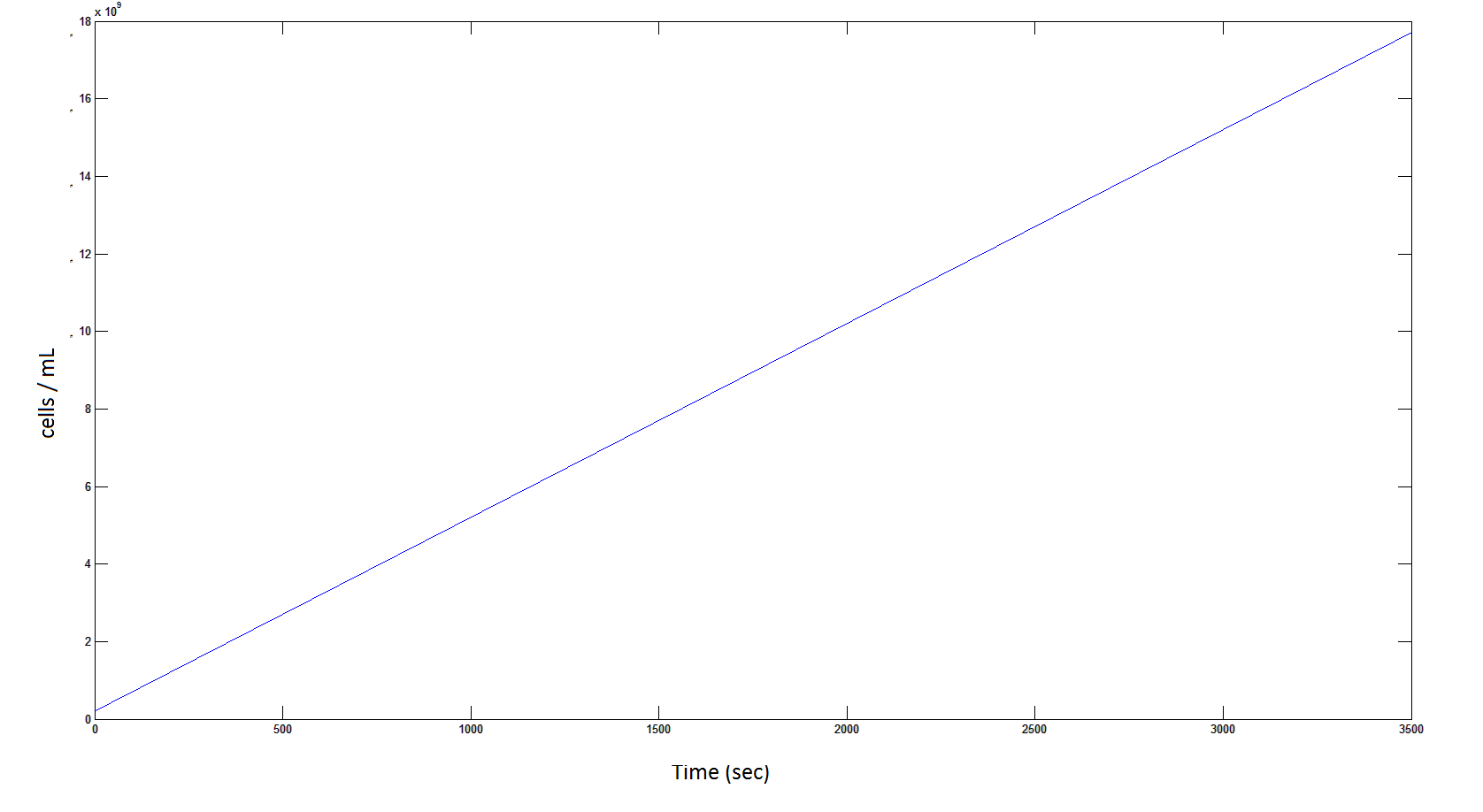
The rate at which the cells grow over time:
Graph 4: the blue line represents the linear increase of cells due to the presence of intracellular glycolate.
The Non-monooxygenase Pathway
ODE overview:
Raw MATLAB code:
function dy = p450(t,y)
dy=zeros(6,1);
dy(1)= -y(6)*(6*10^(-12))*0.0463067*(y(1)-y(2));
dy(2)= ((6*10^(-12))*0.0463067*(y(1)-y(2))) - 0.0113*25.55*(y(2)/(.12+y(2)));
dy(3) = 0.0113*25.55*(y(2)/(.12+y(2))) - 0.6*25.55*(y(3)/(0.16+y(3)));
dy(4)= 0.6*25.55*(y(3)/(0.16+y(3))) - 25.4*25.55*(y(4)/(20+y(4)));
if y(5) > 2*10^(-10)
dy(5)= 25.4*25.55*(y(4)/(20+y(4))) -1.5789*10^(-10)
else
dy(5) = 25.4*25.55*(y(4)/(20+y(4)))
end
if y(5) > 0.0005
if y(6) > 1.6*10^11
dy(6)=0
else
dy(6) = 5*10^6
end
else
dy(6) = 0
end
end
MATLAB output:
The rate at which DCA is removed in solution:
Graph 5: The blue line represents how the concentration of DCA in solution decreases due to the action of our DCA degraders. .
The Rate at which the intracellular concentration of the metabolites change over time:
Graph 6: Each line represents the concentration of each of the metabolites . This graph is simply a rescaling of graph 5.
Rescaling the graph once again: the rate at which the metabolic intermediate change over time.
Graph 7: Each line represents the concentration of each of the metabolites . This graph is simply a rescaling of graph 5 and 6.
The rate at which the cells grow over time:
Graph 8: the blue line represents the linear increase of cells due to the presence of intracellular glycolate.
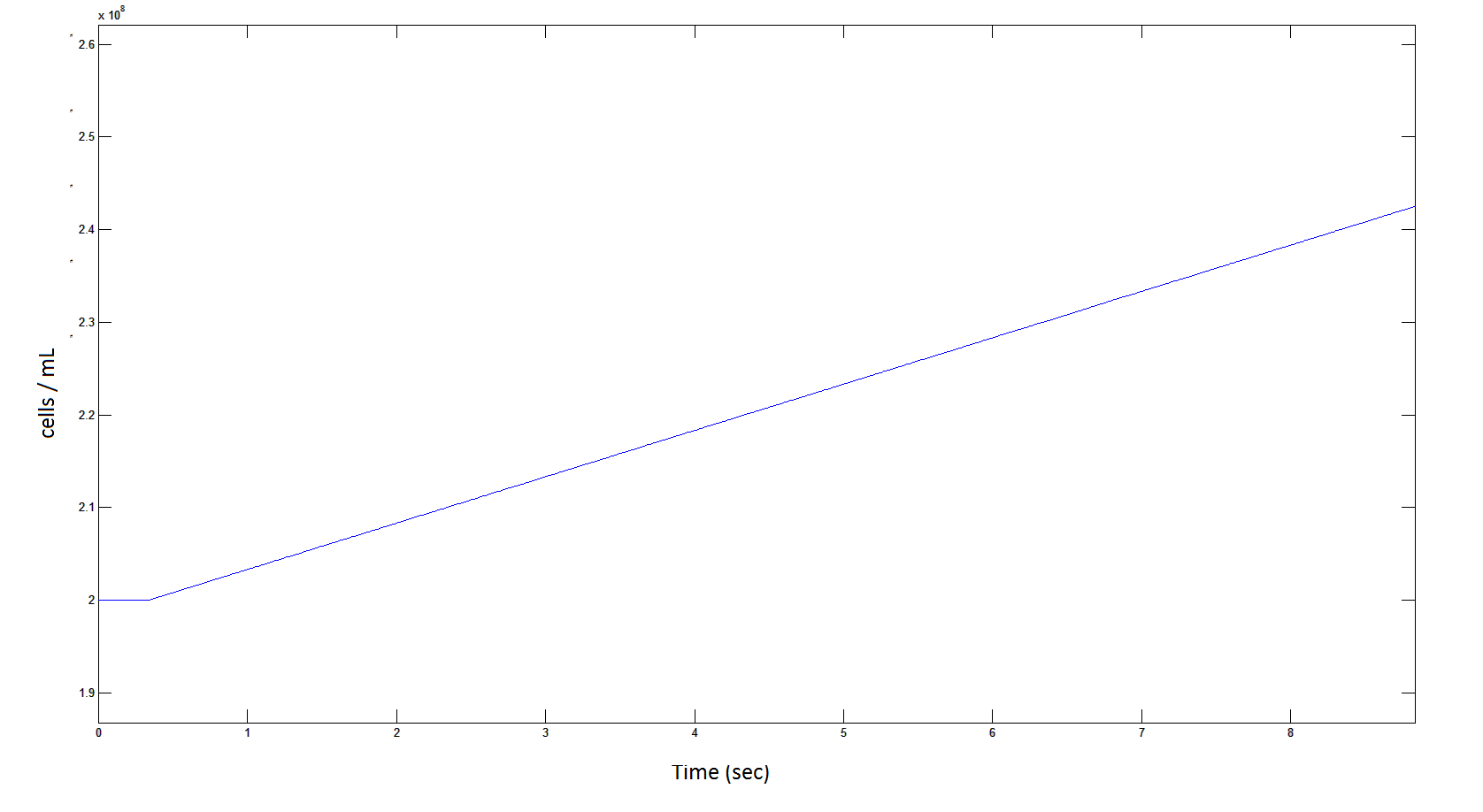
Rescaling Shows a lag effect on cell growth:
Graph 9: the blue line represents the increase of cells due to the presence of intracellular glycolate. This graph is a rescaling of graph 8 to show the inital lag in cellualr growth.
Conclusions:
From Graphs 1 and 5, one can see that 1mM of DCA is removed from solution within roughly 50 minutes.
From Graphs 4, 8 and 9, that bacterial growth occurs, and that this is due to the production of glycolate; this is evident by comparing graphs 6 and 9, where bacterial growth correlates with glycolate accumulation.
The cytotoxic chloroactealdehyde doesn't accumulate to a significant concentration in any of the pathways. From Graphs 3 and 7 one can see that chloroacetaldehyde reaches a maximum concentration of roughly 0.2 mM in both pathways. Chloroacetaldehyde is seen to be metabolised very quickly; this concentration maximum is very short lived where it peaks at roughly 0.03 seconds and returns back to 0 mM by 0.5 seconds. It is expected that chloroacetaldehyde toxicity will not be a problem in our engineered cells.
References:
[1] Krooshof, G. H., Ridder, I. S., Tepper, A. W., Vos, G. J., Rozeboom, H. J., Kalk, K. H., Dijkstra, B. W. & Janssen, D. B. (1998). Kinetic Analysis and X-ray Structure of Haloalkane Dehalogenase with a Modified Halide-Binding Site. Biochemistry, 37(43), 15013-15023.
[2] Janecki, D. J., Bemis, K. G., Tegeler, T. J., Sanghani, P. C., Zhai, L., Hurley, T. D., Bosron, W. F. & Wang, M. (2007). A multiple reaction monitoring method for absolute quantification of the human liver alcohol dehydrogenase ADH1C1 isoenzyme. Analytical Biochemistry, 369(1), 18-26.
[3] Pandey, A. V. & Flück, C. E. (2013). NADPH P450 oxidoreductase: Structure, function, and pathology of diseases. Pharmacology & Therapeutics, 138(2), 229-254.
[4] van der Ploeg, J., Shmidt, M. P., Landa, A. S., & Janssen, D. B. (1994). Identification of Chloroacetaldehyde Dehydrogenase Involved in 1,2-Dichloroethane Degradation. Applied Environmental Microbiology 60(5), 1599-1605.
[5] van der Ploeg, J., van Hall, G. & Janssen, D. B. (1991) Characterization of the haloacid dehalogenase from Xanthobacter autotrophicus GJ10 and sequencing of the dhlB gene. Journal of Bacteriology, 173(24), 7925-33.
[6] Sinensky, M. I. (1974). Homeoviscous Adaption – A Homeostatic Process that Regulates the Viscosity of Membrane Lipids in Escherichia coli. Proceedings from the National Academy of Science of the United States of America, 71(2), 522-525.
[7] CyberCell Database
[8]
[9]
[10] http://www.dtsc.ca.gov/AssessingRisk/Upload/12dca.pdf
[11]
[12]
 "
"