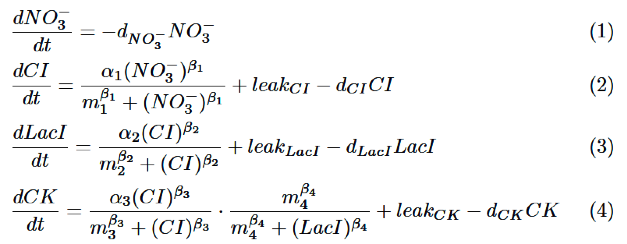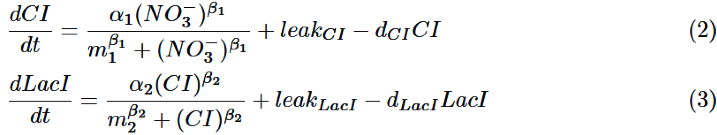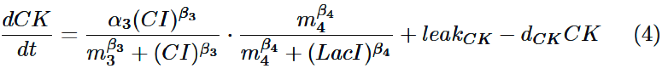Incoherent Feed Forward Loop Modeling

1. Introduction

In order to achieve the natural plants’ temporal pattern for producing plant hormones in E. coli, we introduced an incoherent feed forward loop to our circuit, including a new hybrid promoter part ([http://parts.igem.org/Part:BBa_K1139150 BBa_K1139150]).

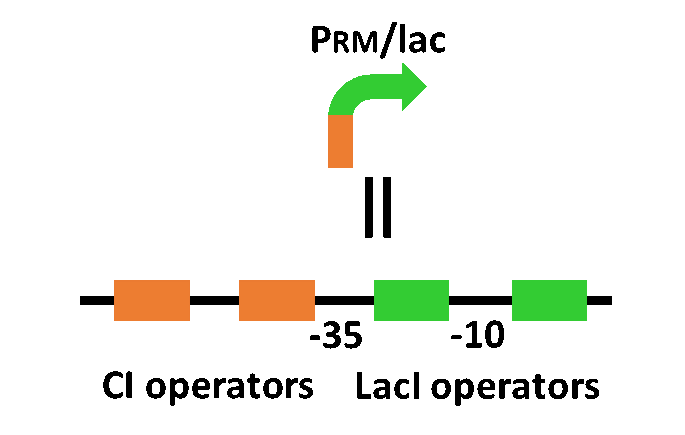
Our designed system with an incoherent feed forward loop is shown in Fig. 4-2-1. We newly developed RM/lac hybrid promoter, which is activated by CI and repressed by LacI (Fig. 4-2-2). We planned to ligate a plant hormone synthase part downstream of this hybrid promoter. While the RM/lac hybrid promoter activation by CI is a single-step reaction, the repression by LacI is a two-step reaction. Thus, the activation of RM/lac hybrid promoter is faster than the repression. This time lag between the activation and the repression is important for generating a temporal pattern of plant hormone production.

Fig. 4-2-1. Our designed system with an incoherent feed forward loop

Fig. 4-2-2. Our newly designed hybrid promoter

By the following mathematical model, we predicted that we can achieve pulse-generation of cytokinin as an output, using nitric acid (NO₃^-) as an input. In addition, we analyzed the relation between the waveform and the expression level of LacI.

2. Dynamic behavior of our circuit

2-1. Building a mathematical model

Our model is described by the following differential equations based on Hill equation.

Fig. 4-2-3. Equations for our modeling

We will explain each equation.

As for NO₃^-, we only take the degradation into consideration, assuming that NO₃^- act directly on nitrate promoter.

Fig. 4-2-4. Equation of NO₃^-

CI is activated by NO₃^-, LacI is activated by CI. Behaviors of CI and LacI are described by equation (2) and (3).

Fig. 4-2-5. Equations of CI and LacI

Finally, behavior of RM/lac hybrid promoter is shown as multiplication of the activation by CI and the repression by LacI. Therefore, the dynamics of cytokinin is described by equation (4).

Fig. 4-2-6. Equation of cytokinin

We set the parameters as follows:

Fig. 4-2-7. Descriptions of the parameters

The values of the parameters are set as follows:

Fig. 4-2-8. Values of the parameters

2-2. Simulation results of the incoherent feed forward loop

Fig. 4-2-9 shows the simulation results about the relation between the input (NO₃^-) and the output (cytokinin) in our circuit. The red line represents the concentration of NO₃^-, the green line represents the concentration of cytokinin.

Fig. 4-2-9. Time-dependent change of the concentrations of NO₃^- and cytokinin

As shown in Fig. 4-2-9, we verified the pulse-generation of cytokinin as the output. We will discuss the process of the pulse-generation by looking at the expression level of each substance.

First, NO₃^- as an input activates CI. CI continues to increase until the input is completely degraded because the expression level of CI depends on the volume of the input (Fig. 4-2-10).

Fig. 4-2-10. Time-dependent change of the concentrations of NO₃^- and CI

Next, Fig. 4-2-11 shows that LacI and cytokinin are activated by CI. Also, in Fig. 4-2-12, which shows the enlarged view of Fig. 4-2-11 around 0 min., LacI is expressed after the expression of CI.

Fig. 4-2-11. Time-dependent change of the concentrations of CI, LacI and cytokinin

Fig. 4-2-12. Enlarged view of Fig. 4-2-11.

Finally, Fig. 4-2-11 also shows that cytokinin is repressed by LacI after it is activated by CI. Cytokinin is expressed during this time lag between the activation and the repression.

2-3. Relation between the waveform and the maximum level

of the LacI expression

In 2-2, we confirmed that the expression of LacI is deeply concerned with the expression of cytokinin. Here, we analyzed the waveform of the cytokinin output by changing the maximum level of the LacI expression (α2). Fig. 4-2-13 shows the change in the waveforms of cytokinin depending on the maximum level of LacI expression.

Fig. 4-2-13. Waveforms of cytokinin depending on the maximum level of LacI expression

We see that the waveform of the cytokinin output changes depending on the maximum level of the LacI expression. In considering the application of this system, we predict that we can adapt the output waveforms to the circumstances of plants.

2-4. Relation between the output waveform and IPTG

Here, we will predict the activity of LacI by considering the volume of IPTG, which represses LacI. Decrease in LacI activity is described by equation (5). (γ denotes the decay rate constant.)

Fig. 4-2-14. Equation of decreasing LacI activity

Substituting equation (5) for equation (4), we obtain equation (6).

Fig. 4-2-15. Equation of cytokinin led from equation (4) and (5)

Shown in equation (6), the pulse width of the cytokinin expression can be controlled by external IPTG. In the simulation by changing the value of γ, we obtained the result shown in Fig. 4-2-16.

Fig. 4-2-16. Changes of the cytokinin expression time controlled by IPTG

Therefore, we confirmed that the pulse width of the cytokinin expression can be controlled by the volume of IPTG.