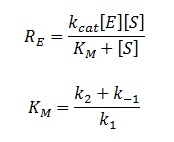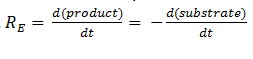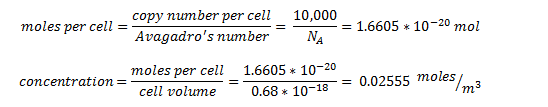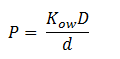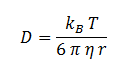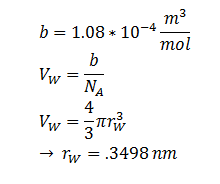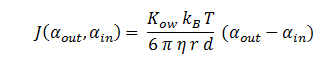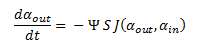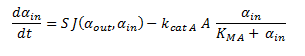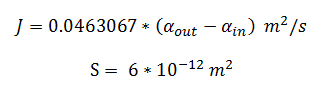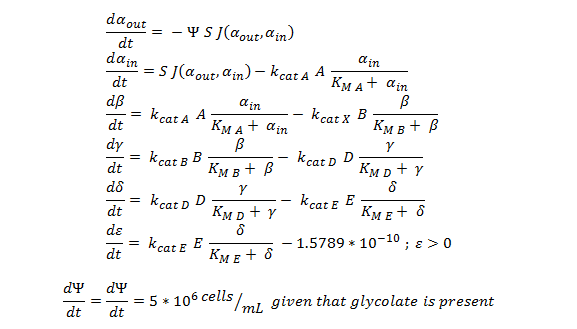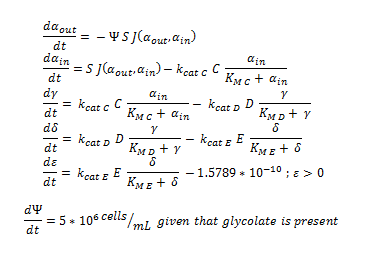Team:SydneyUni Australia/Modelling Validation
From 2013.igem.org
Jbergfield (Talk | contribs) (Created page with "{{Team:SydneyUni_Australia/Style}} {{Team:SydneyUni_Australia/Header}} __NOTOC__ =='''Running the Model'''== The model was run using MATLAB through the ode solver ODE45. Th...") |
|||
| Line 1: | Line 1: | ||
{{Team:SydneyUni_Australia/Style}} | {{Team:SydneyUni_Australia/Style}} | ||
{{Team:SydneyUni_Australia/Header}} | {{Team:SydneyUni_Australia/Header}} | ||
| + | |||
| + | |||
| + | |||
| + | =='''Constructing a model for the metabolic pathway'''== | ||
| + | |||
| + | The rate of change for the intracellular concentration of metabolites (β, γ, δ and ε) is purely determined through the relative activity (described by MM equations) of the enzymes creating or removing the metabolite. | ||
| + | |||
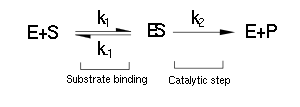
| + | Luckily the enzymes of our metabolic pathway are accurately described by MM kinetics and all constants were available in the literature. The system is based on the forward and reverse kinetic rate (k<sub>1</sub> and k<sub>-1</sub> respectively) of substrate-enzyme binding followed by the irreversible catalytic step of product formation (k<sub>2</sub>) as depicted in the figure below: | ||
| + | |||
| + | [[File:Igem pathway 1.png|center]] | ||
| + | |||
| + | The rate of catalysis for an enzyme is a function of the enzyme and substrate concentration and incorporates the catalytic constant k<sub>cat</sub> and the Michaelis constant K<sub>M</sub>, which are given in most enzyme kinetics studies. | ||
| + | |||
| + | [[File:Igem Re.jpg|center]] | ||
| + | |||
| + | The symbol R<sub>E</sub> denotes the reaction rate: i.e. the rate of product formation (which is equal to the rate of substrate removal). | ||
| + | |||
| + | [[File:Igem Re= dproduct.png|center]] | ||
| + | |||
| + | So, by observing: | ||
| + | |||
| + | i) that the rate at which a substrate is removed is directly equal to the rate at which the associated product is created (e.g. the rate at which γ is removed is the rate at which δ is formed) | ||
| + | ii) and how each intermediate simultaneously acts as a substrate and product (e.g. how D creates δ, and E uses δ to create ε) | ||
| + | |||
| + | it is easy to see how this process gives rise to a connected system of ODEs. | ||
| + | |||
| + | |||
| + | =='''Estimating Protein Concentration'''== | ||
| + | |||
| + | The accuracy of this model is strongly dependent on the intracellular enzyme concentrations; these cannot be determined theoretically as there is a weak correlation with the level of gene expression and protein abundance. | ||
| + | |||
| + | Ishihama <i>et al.</i> ([11]) profiled the protein concentration in <i>E. coli</i> as: | ||
| + | |||
| + | [[File: why was ET brown?.png|center]] | ||
| + | |||
| + | The enzyme-encoding-genes are under the regulation of an artificial promoter termed Psyn. The promoter is designed to be constitutive and drive high expression of the enzymes. We estimated the protein concentration as 10,000 protein units per cell - the upper quartile limit in the ‘Highly abundant group’ box in the figure above. | ||
| + | |||
| + | By taking the cell volume as 0.65µ<sup>3</sup> = 0.63 x 10<sup>-18</sup> m<sup>3</sup> [7] | ||
| + | [[File: pikachu is simply a mouse that sneezes electricity.png|center]] | ||
| + | |||
| + | So the intracellular concentration for all proteins is predicted to be 25.55 mM | ||
| + | |||
| + | |||
| + | =='''DCA Diffusion Across the Plasma Membrane'''== | ||
| + | |||
| + | We were presented with a scenario where it was necessary to model how DCA would move from the solution into the cell where it’s metabolised: i.e. linking α<sub>out</sub> and α<sub>in</sub>. | ||
| + | |||
| + | This was tackled by modelling the rate of DCA diffusion across a cell membrane through Fick’s first law of diffusion: | ||
| + | |||
| + | [[File:j=p.png|center]] | ||
| + | |||
| + | Fick’s first law of diffusion is justified since 1,2-DCA is non-polar and the cellular membrane is thin. The law states that the flux, J, of DCA across the membrane is equal to the permeability coefficient, P, times the concentration difference of DCA across the cell membrane. The flux has units m<sup>2</sup> s<sup>-1</sup> | ||
| + | The permeability coefficient of DCA is not reported in the literature, so it had to be estimated from the definition of the permeability constant. | ||
| + | |||
| + | |||
| + | [[File:p=kow.png|center]] | ||
| + | |||
| + | Where D is the diffusion constant for DCA diffusion across the plasma membrane and d is the length of the membrane. | ||
| + | The partition coefficient for DCA across a plasma membrane is not documented, but can be estimated to be similar to the octanol-water partition coefficient (K<sub>ow</sub>). This constant determines the equilibrium ratio of DCA in octanol and water. | ||
| + | Like many properties of DCA, the diffusion constant, D, is not documented in the literature. It was determined through the famous Stokes-Einstein equation: | ||
| + | |||
| + | |||
| + | [[File:D=kb.png|center]] | ||
| + | |||
| + | Where k<sub>B</sub>, T, η & r represent the Boltzmann constant (1.3806488 × 10-23 m<sup>2</sup> kg s-2 K-1), temperature, viscosity of the membrane and radius of DCA respectively. Here we must assume DCA is spherical. | ||
| + | The ‘radius’ of DCA isn’t described in the literature. But the van der Waal constant, b, can be used to calculate the van der Waal volume, V<sub>W</sub> , and hence the van der Waal radius, r<sub>W</sub><sup>3</sup>. Note DCA is not spherical, and this method is used to calculate atoms. | ||
| + | |||
| + | [[File:Igem b=.png|center]] | ||
| + | |||
| + | By combining all of the above, the flux can be described as: | ||
| + | |||
| + | [[File:Igem summary J=.png|center]] | ||
| + | |||
| + | |||
| + | |||
| + | <center>'''Summary of Constants'''</center> | ||
| + | |||
| + | <center> | ||
| + | {|class="wikitable" | ||
| + | !Symbol !! Name !! Value (units) !! Ref | ||
| + | |- | ||
| + | |η || Cellular Membrane Viscosity || 1.9 kg/m/s || [6] | ||
| + | |- | ||
| + | |S || E. coli Membrane Surface Area || 6x10<sup>-12</sup> m<sup>2</sup> || [7] | ||
| + | |- | ||
| + | |r || DCA radius || 0.3498 nm || [8] | ||
| + | |- | ||
| + | |K<sub>ow</sub> || Octanol-water Partition Coefficient for DCA || 28.2 || [9] | ||
| + | |- | ||
| + | |d || Length of Cellular Membrane || 2 nm || [10] | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | =='''Extending the System to Cell Cultures'''== | ||
| + | |||
| + | The model describes the process of DCA diffusion and metabolism of a single cell. So given a concentration of our engineered cells in solution one can calculate the rate at which the DCA concentration in solution (αα<sub>out</sub>) decreases by simply multiply the flux rate of DCA across the membrane by the total concentration of cells in the solution. | ||
| + | So, by letting Ψ represent the concentration of cells in solution. The overall rate of decrease of DCA in solution is: | ||
| + | |||
| + | [[File:Igem datot=daout1213.png|center]] | ||
| + | |||
| + | Since the latter portion of the system of ODEs describes the intracellular concentrations within a single cell, the rate at which the DCA comes into the cell and is metabolised (dα<sub>in</sub>/dt) is simply: | ||
| + | |||
| + | [[File: simply is a simply simple word.png|center]] | ||
| + | |||
| + | |||
| + | The motivation for doing this as it seems more natural to consider the intracellular metabolite concentrations of a single cell, rather than averaged across many. It also allows one to gauge whether chloroacetaldehyde reaches cytotoxic levels. The assumption made here is that all the cells in the solution are exactly the same. | ||
| + | |||
| + | =='''Factoring in Cell Growth'''== | ||
| + | |||
| + | The cells are expected to grow due to the production of glycolate (used as a carbon source for growth). So one can model the rate at which the cell concentration, Ψ, increases. | ||
| + | Ideally one would want to experimentally determine the cell growth as function of time, but unfortunately we did not have enough time to do this. | ||
| + | We turned to other, more approximate measures: | ||
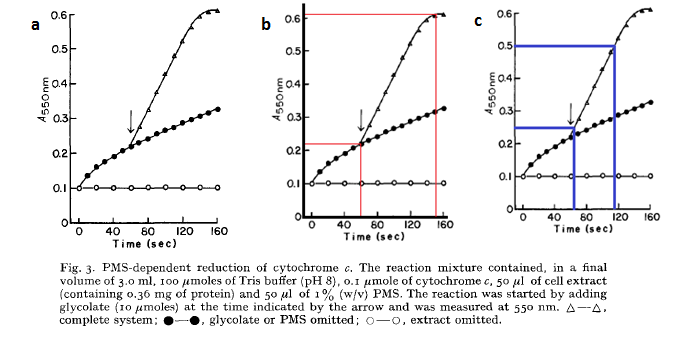
| + | The growth of <i>E. coli</i> over time due to the presence of glycolate was initially described by Lord [12]: | ||
| + | |||
| + | |||
| + | [[File: ned flanders.png|center]] | ||
| + | |||
| + | Firstly it must be noted that this analysis is highly approximate, and is used only to obtain a very rough estimate of the growth rate as a function of glycolate produced. | ||
| + | By using the approximation that an OD550 of 0.1 = 1 x 10<sup>8</sup> cells/mL one can use the above graph to generate rates of E. coli growth due to glycolate production. | ||
| + | From graph 1, it can be seen that a 2.2 x 10<sup>8</sup>cells us 3.33 mM of glycolate in 95 seconds. Or in other words, 1 cell uses 1.5789 x 10<sup>-10</sup> mM of glycolate per second: | ||
| + | |||
| + | [[File: jakethedog.png|center]] | ||
| + | |||
| + | This assumes that only the original cells existing in solution from the graphs above (the 2.2E8 cells) use glycolate for growth. | ||
| + | From the graph b, the OD550 increases at a rate of 0.25 per 50 seconds (gradient of graph 2) which shows that the cells increase at a maximum rate of 5x10<sup>6</sup> cells / mL / s when growing in saturated glycolate. | ||
| + | From the graphs, it can be seen that the point where maximal growth no longer occurs (where the straight line becomes curved) is when glycolate is at a very low concentration. We will take it that the saturation point is so small that it is negligible – i.e. the growth rate is always maximal when in the presence of glycolate. | ||
| + | So the cellular growth rate can be described as: | ||
| + | |||
| + | [[File: finthehuman.png|center]] | ||
| + | |||
| + | Using this approach, the model for growth rate is most appropriate for cell concentrations in the range of 2 x 10<sup>8</sup> to 6 x 10<sup>8</sup> cells/mL. | ||
| + | |||
| + | |||
| + | |||
| + | {{Team:SydneyUni_Australia/Footer}} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
__NOTOC__ | __NOTOC__ | ||
Revision as of 06:55, 27 October 2013


Constructing a model for the metabolic pathway
The rate of change for the intracellular concentration of metabolites (β, γ, δ and ε) is purely determined through the relative activity (described by MM equations) of the enzymes creating or removing the metabolite.
Luckily the enzymes of our metabolic pathway are accurately described by MM kinetics and all constants were available in the literature. The system is based on the forward and reverse kinetic rate (k1 and k-1 respectively) of substrate-enzyme binding followed by the irreversible catalytic step of product formation (k2) as depicted in the figure below:
The rate of catalysis for an enzyme is a function of the enzyme and substrate concentration and incorporates the catalytic constant kcat and the Michaelis constant KM, which are given in most enzyme kinetics studies.
The symbol RE denotes the reaction rate: i.e. the rate of product formation (which is equal to the rate of substrate removal).
So, by observing:
i) that the rate at which a substrate is removed is directly equal to the rate at which the associated product is created (e.g. the rate at which γ is removed is the rate at which δ is formed) ii) and how each intermediate simultaneously acts as a substrate and product (e.g. how D creates δ, and E uses δ to create ε)
it is easy to see how this process gives rise to a connected system of ODEs.
Estimating Protein Concentration
The accuracy of this model is strongly dependent on the intracellular enzyme concentrations; these cannot be determined theoretically as there is a weak correlation with the level of gene expression and protein abundance.
Ishihama et al. ([11]) profiled the protein concentration in E. coli as:
The enzyme-encoding-genes are under the regulation of an artificial promoter termed Psyn. The promoter is designed to be constitutive and drive high expression of the enzymes. We estimated the protein concentration as 10,000 protein units per cell - the upper quartile limit in the ‘Highly abundant group’ box in the figure above.
By taking the cell volume as 0.65µ3 = 0.63 x 10-18 m3 [7]
So the intracellular concentration for all proteins is predicted to be 25.55 mM
DCA Diffusion Across the Plasma Membrane
We were presented with a scenario where it was necessary to model how DCA would move from the solution into the cell where it’s metabolised: i.e. linking αout and αin.
This was tackled by modelling the rate of DCA diffusion across a cell membrane through Fick’s first law of diffusion:
Fick’s first law of diffusion is justified since 1,2-DCA is non-polar and the cellular membrane is thin. The law states that the flux, J, of DCA across the membrane is equal to the permeability coefficient, P, times the concentration difference of DCA across the cell membrane. The flux has units m2 s-1 The permeability coefficient of DCA is not reported in the literature, so it had to be estimated from the definition of the permeability constant.
Where D is the diffusion constant for DCA diffusion across the plasma membrane and d is the length of the membrane. The partition coefficient for DCA across a plasma membrane is not documented, but can be estimated to be similar to the octanol-water partition coefficient (Kow). This constant determines the equilibrium ratio of DCA in octanol and water. Like many properties of DCA, the diffusion constant, D, is not documented in the literature. It was determined through the famous Stokes-Einstein equation:
Where kB, T, η & r represent the Boltzmann constant (1.3806488 × 10-23 m2 kg s-2 K-1), temperature, viscosity of the membrane and radius of DCA respectively. Here we must assume DCA is spherical. The ‘radius’ of DCA isn’t described in the literature. But the van der Waal constant, b, can be used to calculate the van der Waal volume, VW , and hence the van der Waal radius, rW3. Note DCA is not spherical, and this method is used to calculate atoms.
By combining all of the above, the flux can be described as:
| Symbol | Name | Value (units) | Ref |
|---|---|---|---|
| η | Cellular Membrane Viscosity | 1.9 kg/m/s | [6] |
| S | E. coli Membrane Surface Area | 6x10-12 m2 | [7] |
| r | DCA radius | 0.3498 nm | [8] |
| Kow | Octanol-water Partition Coefficient for DCA | 28.2 | [9] |
| d | Length of Cellular Membrane | 2 nm | [10] |
Extending the System to Cell Cultures
The model describes the process of DCA diffusion and metabolism of a single cell. So given a concentration of our engineered cells in solution one can calculate the rate at which the DCA concentration in solution (ααout) decreases by simply multiply the flux rate of DCA across the membrane by the total concentration of cells in the solution. So, by letting Ψ represent the concentration of cells in solution. The overall rate of decrease of DCA in solution is:
Since the latter portion of the system of ODEs describes the intracellular concentrations within a single cell, the rate at which the DCA comes into the cell and is metabolised (dαin/dt) is simply:
The motivation for doing this as it seems more natural to consider the intracellular metabolite concentrations of a single cell, rather than averaged across many. It also allows one to gauge whether chloroacetaldehyde reaches cytotoxic levels. The assumption made here is that all the cells in the solution are exactly the same.
Factoring in Cell Growth
The cells are expected to grow due to the production of glycolate (used as a carbon source for growth). So one can model the rate at which the cell concentration, Ψ, increases. Ideally one would want to experimentally determine the cell growth as function of time, but unfortunately we did not have enough time to do this. We turned to other, more approximate measures: The growth of E. coli over time due to the presence of glycolate was initially described by Lord [12]:
Firstly it must be noted that this analysis is highly approximate, and is used only to obtain a very rough estimate of the growth rate as a function of glycolate produced. By using the approximation that an OD550 of 0.1 = 1 x 108 cells/mL one can use the above graph to generate rates of E. coli growth due to glycolate production. From graph 1, it can be seen that a 2.2 x 108cells us 3.33 mM of glycolate in 95 seconds. Or in other words, 1 cell uses 1.5789 x 10-10 mM of glycolate per second:
This assumes that only the original cells existing in solution from the graphs above (the 2.2E8 cells) use glycolate for growth. From the graph b, the OD550 increases at a rate of 0.25 per 50 seconds (gradient of graph 2) which shows that the cells increase at a maximum rate of 5x106 cells / mL / s when growing in saturated glycolate. From the graphs, it can be seen that the point where maximal growth no longer occurs (where the straight line becomes curved) is when glycolate is at a very low concentration. We will take it that the saturation point is so small that it is negligible – i.e. the growth rate is always maximal when in the presence of glycolate. So the cellular growth rate can be described as:
Using this approach, the model for growth rate is most appropriate for cell concentrations in the range of 2 x 108 to 6 x 108 cells/mL.
With thanks to:
Running the Model
The model was run using MATLAB through the ode solver ODE45.
The modelling for both the pathays had initial conditions of:
| Constant | Value | Comment |
|---|---|---|
| KM A | 0.530 mM | From literature [1] |
| kcat A | 3.3 s-1 | From literature [1] |
| KM B | 0.940 mM | From literature [2] |
| kcat B | 0.0871 s-1 | From literature [2] |
| KM C | 7.2 mM | From literature [3] |
| kcat c | 89.8 s-1 | From literature [3] |
| KM D | 0.160 mM | From literature [4] |
| kcat D | 0.600 s-1 | From literature [4] |
| KM E | 20 mM | From literature [5] |
| kcat E | 25.4 s-1 | From literature [5] |
| β, γ, δ & ε | 0 mM | Not naturally present in cells. |
| αout | 1 mM | Initial concentration of DCA in solution (arbitrary) |
| αin | 0.001 mM | Initial concentration of DCA in cell |
| A, B, C, D, E | 25.55 mM | Estimation from literature [11], as described in "principles". |
| 2 x 108 cells / mL | Initial cell concentration which allows appropriate growth |
Physical conditions: the model assumes that the cells are present in minimal media prior to DCA exposure and that the DCA is instantaneously and evenly present at time = 0 min in a solution of homogeneously mixed cells
Many assumptions have been made in the construction of the model and are outlined in the 'principles' section.
By using the constants summarised in the previous section the flux, J, took the value (alongside the bacterial surface area, S):
The Non-monooxygenase Pathway
ODE overview:
The summary of the ODE (explained and justified in the previous section).
Raw MATLAB code:
function dy = nop450(t,y)
dy=zeros(7,1);
dy(1)= -y(7)*(6*10^(-12))*0.0463067*(y(1)-y(2));
dy(2)= ((6*10^(-12))*0.0463067*(y(1)-y(2)))-3.3*25.55*(y(2)/(0.53+y(2)));
dy(3)= 3.3*25.55*(y(2)/(0.53+y(2)))-0.0871*25.55*(y(3)/(0.94+y(3)));
dy(4)= .0871*25.55*(y(3)/(0.94+y(3)))- 0.6*25.55*(y(4)/(0.16+y(4)));
dy(5)= 0.6*25.55*(y(4)/(0.16+y(4))) - 25.4*25.55*(y(5)/(20+y(5)));
if y(6) > 2*10^(-10)
dy(6)= 25.4*25.55*(y(5)/(20+y(5))) -1.5789*10^(-10)
else
dy(6) = 25.4*25.55*(y(5)/(20+y(5)))
end
if y(6) > 0.0005
if y(7) > 1.6*10^11
dy(7)=0
else
dy(7) = 5*10^6
end
else
dy(7) = 0
end
end
MATLAB output:
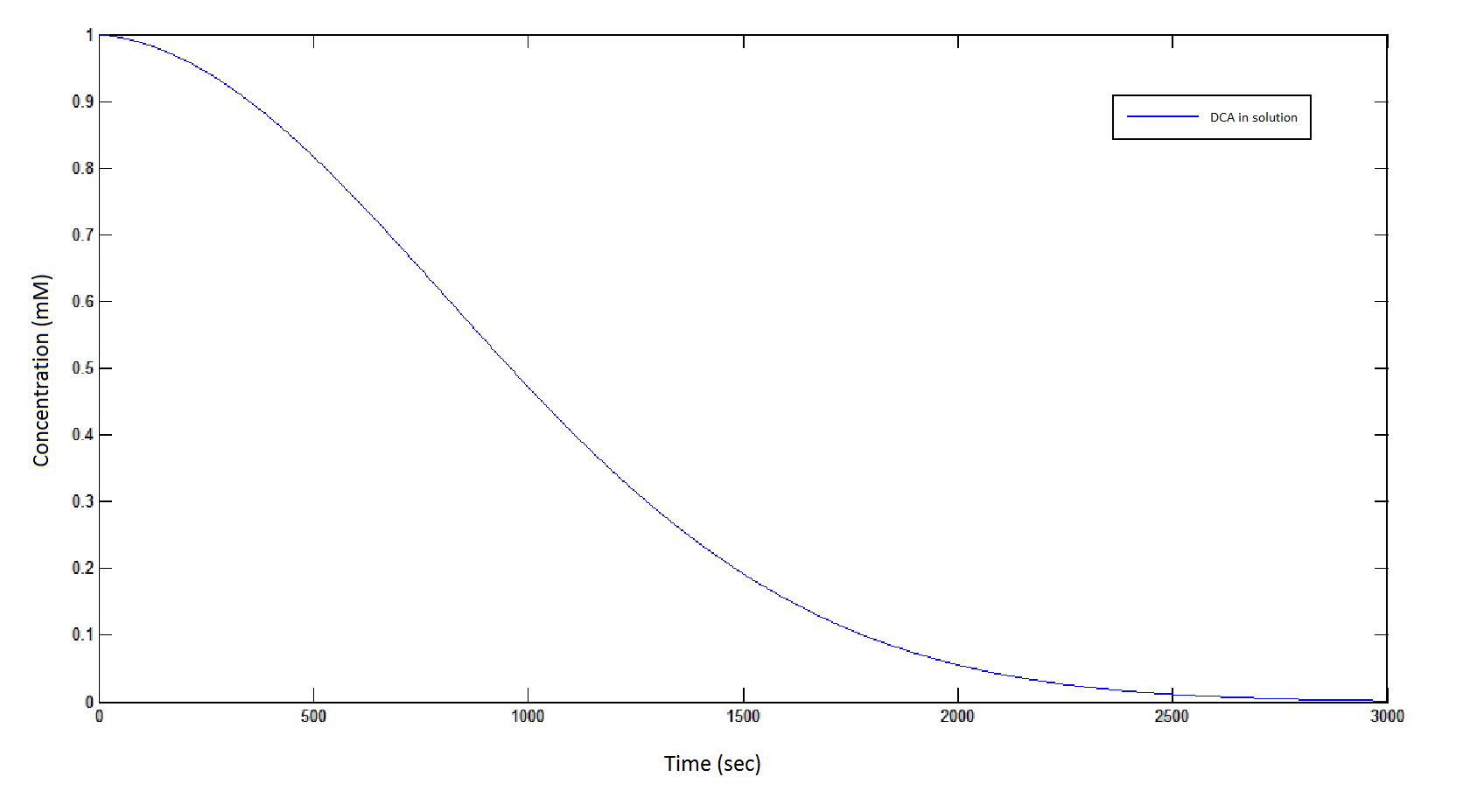
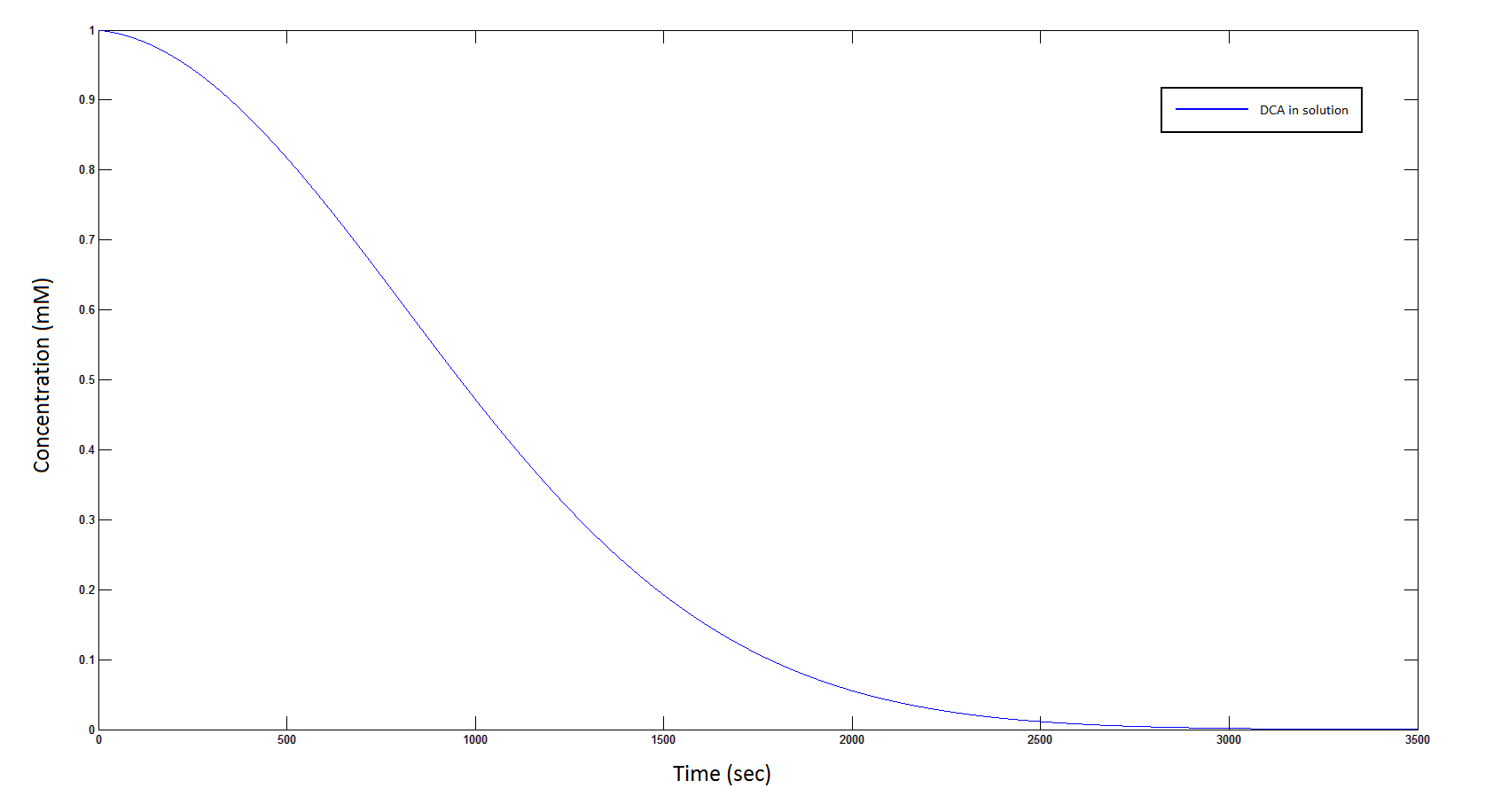
The rate at which DCA is removed in solution:
Graph 1: The blue line represents how the concentration of DCA in solution (extracellular) decreases due to the action of our DCA degraders. The red line represents the intracellular concentions of the metabolites (disregard in this graph). One can see that an initial concentration of 2E8 cells/mL completely removes the DCA with a concentration 1mM in (roughly) 150mins.
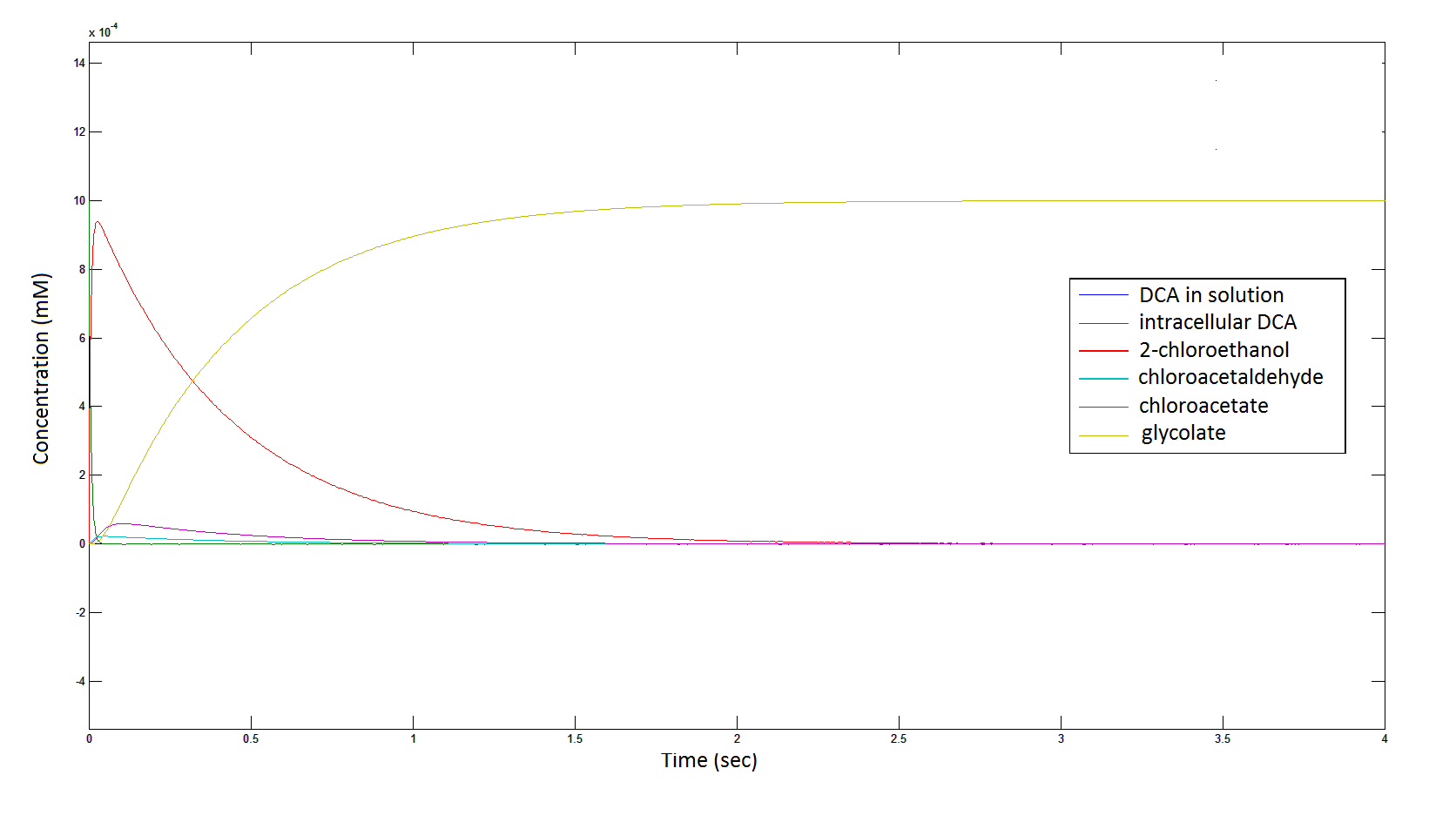
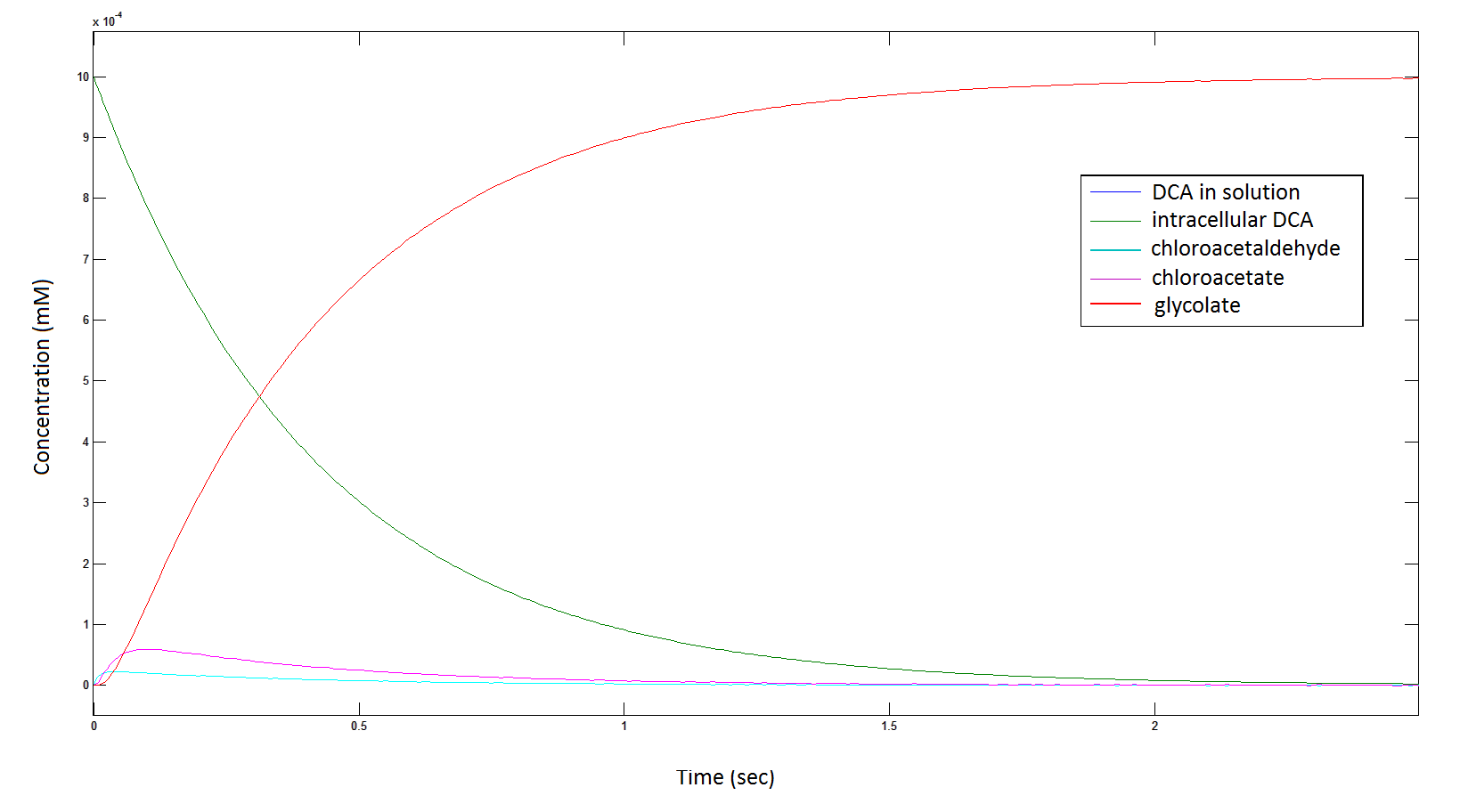
The Rate at which the intracellular concentration of the metabolites change over time:
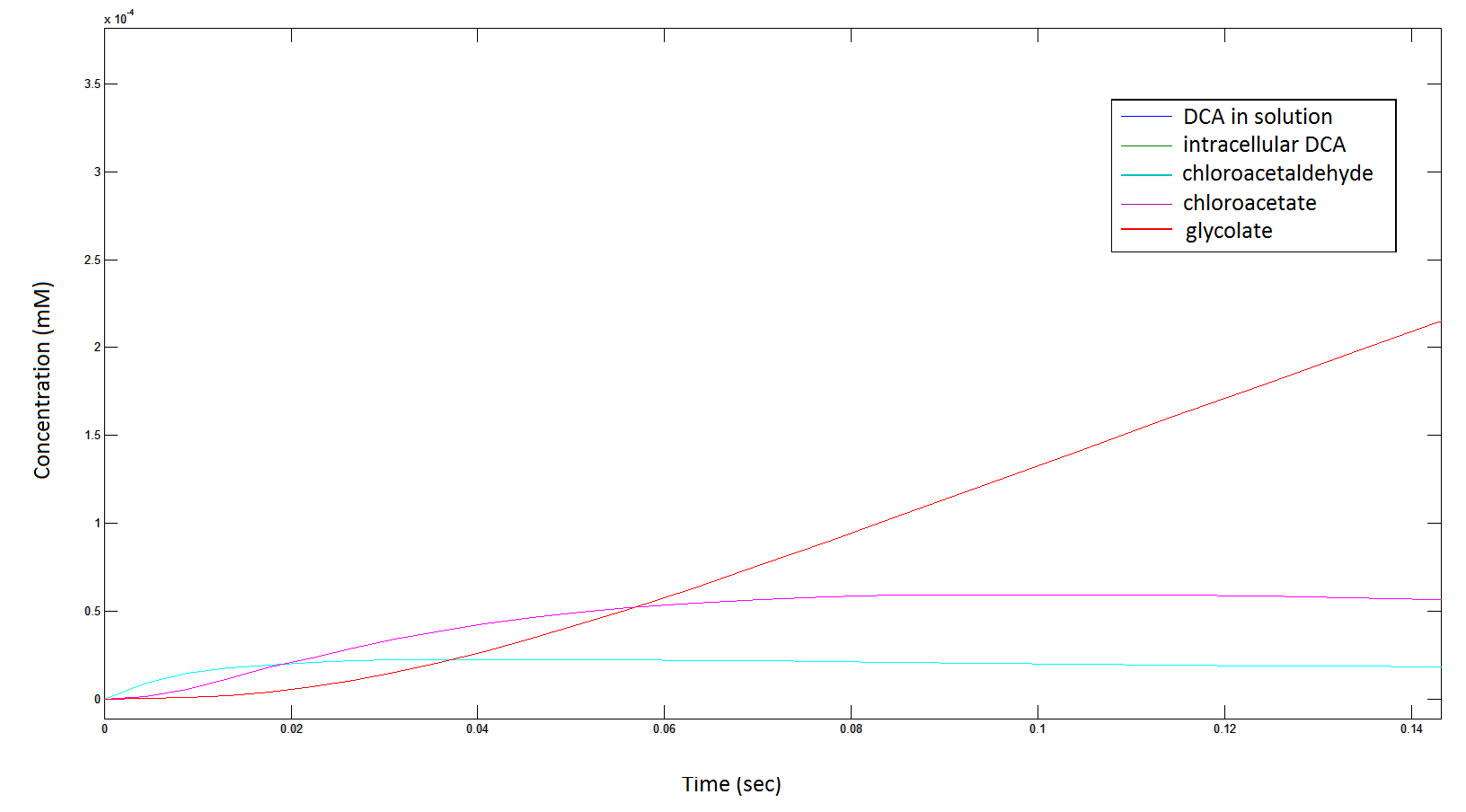
Graph 2: Each line represents the concentration of each of the metabolites . This graph is simply a rescaling of graph 1. Note: the glycolate won’t accumulate in the cell – it is metabolised – the model had glycolate as the final product. It is used to show that the presence of glycolate can attribute to cell growth.
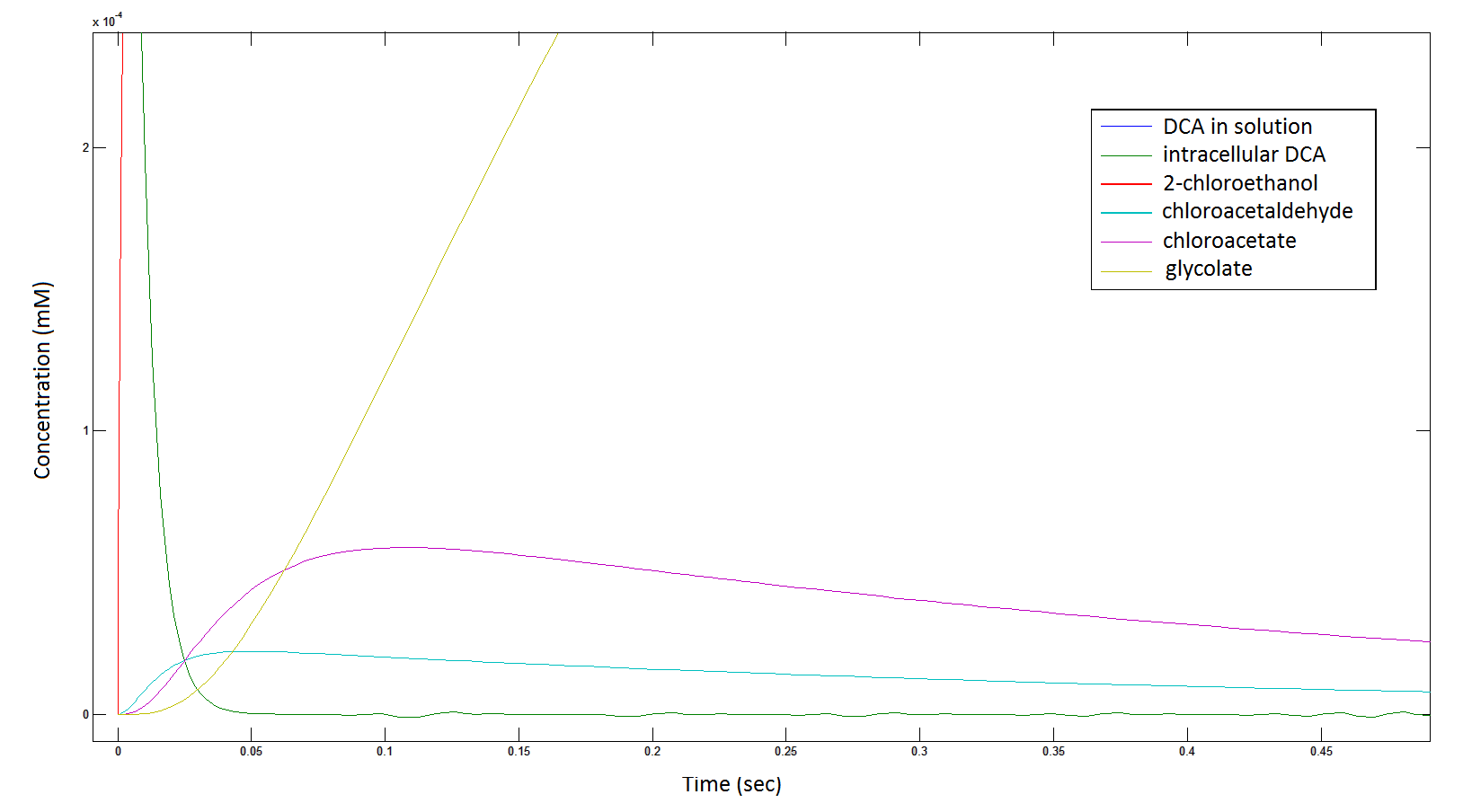
Rescaling the graph once again: the rate at which the metabolic intermediate change over time.
Graph 3: Each line represents the concentration of each of the metabolites . This graph is simply a rescaling of graph 1 and 2.
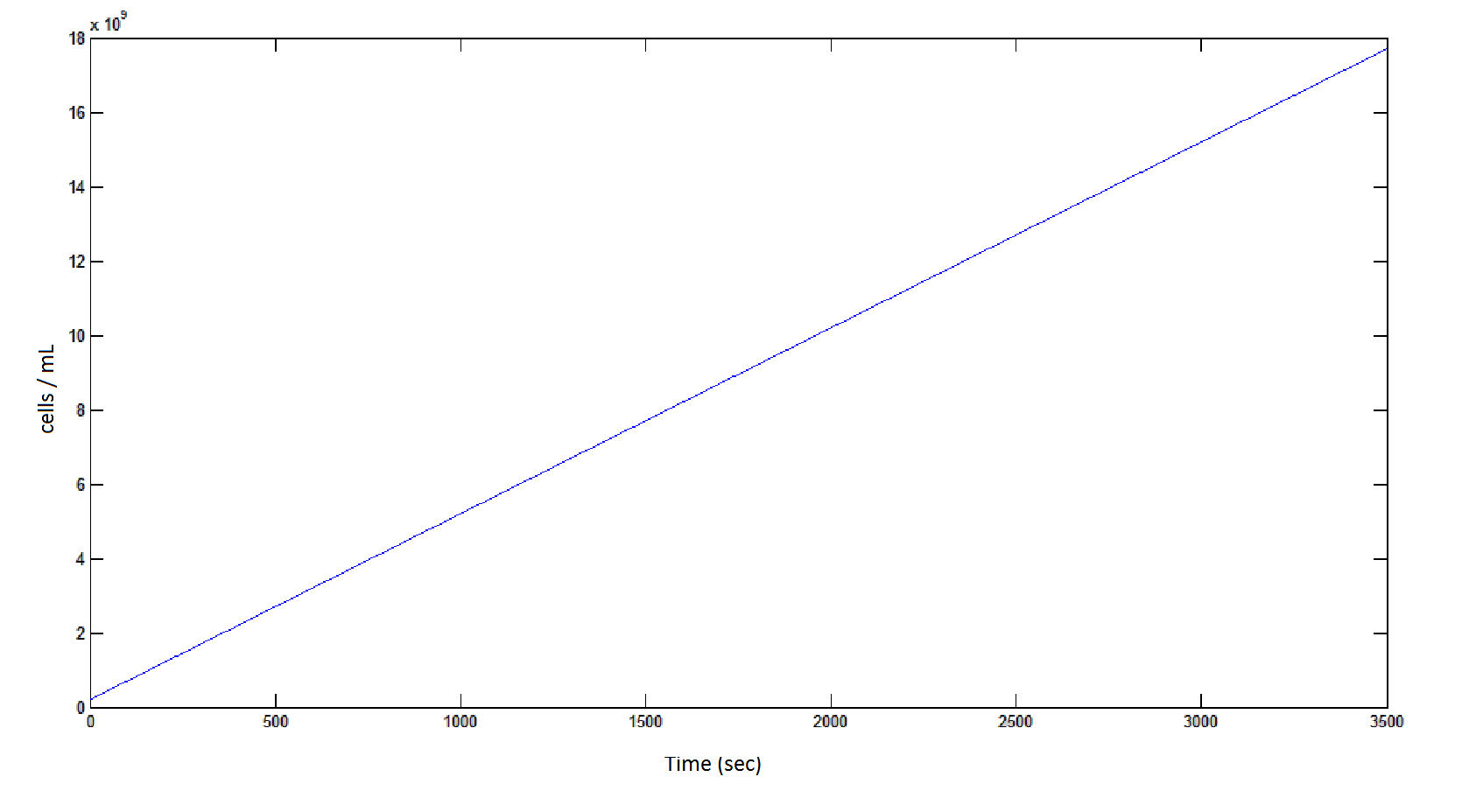
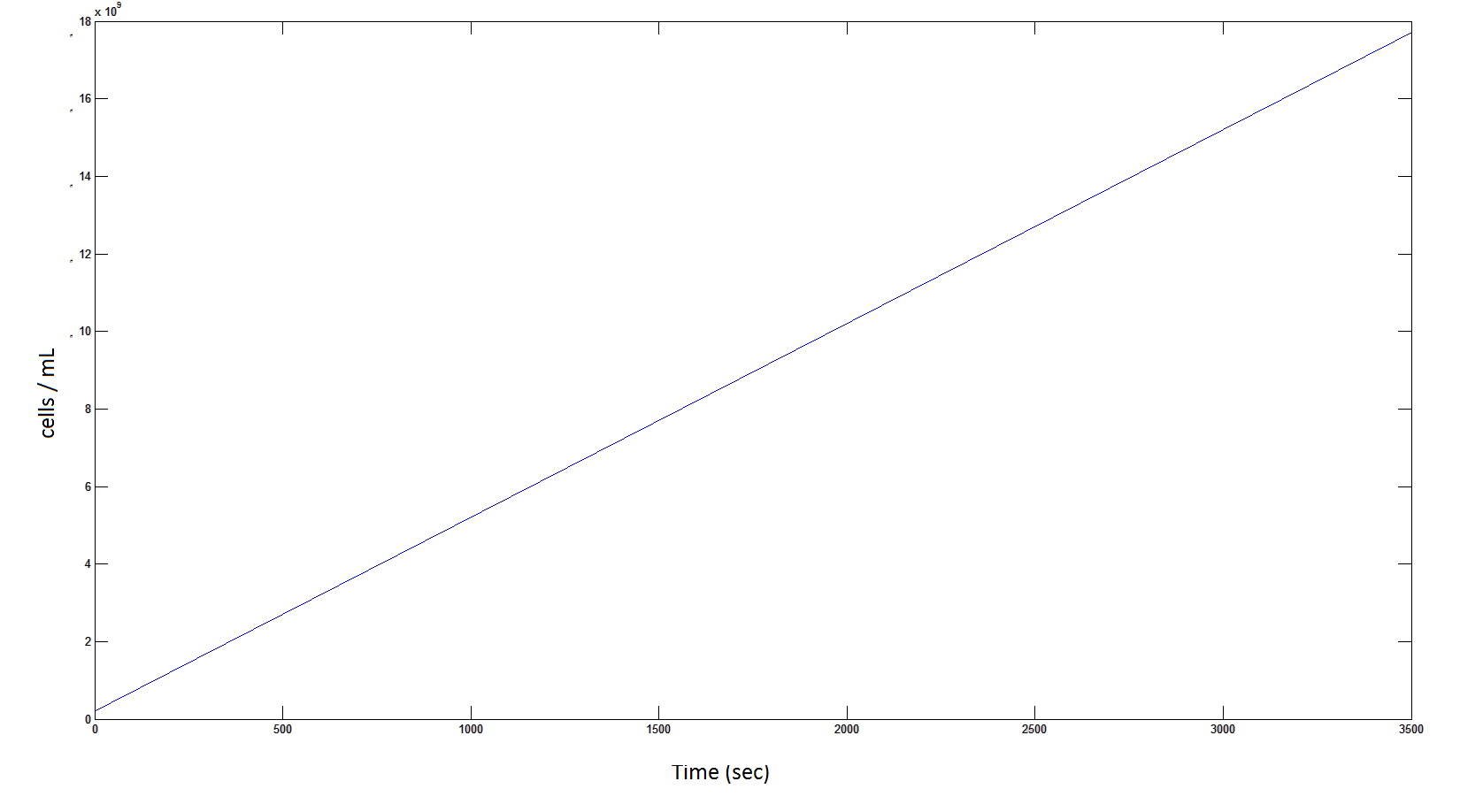
The rate at which the cells grow over time:
Graph 4: the blue line represents the linear increase of cells due to the presence of intracellular glycolate.
The Non-monooxygenase Pathway
ODE overview:
Raw MATLAB code:
function dy = p450(t,y)
dy=zeros(6,1);
dy(1)= -y(6)*(6*10^(-12))*0.0463067*(y(1)-y(2));
dy(2)= ((6*10^(-12))*0.0463067*(y(1)-y(2))) - 0.0113*25.55*(y(2)/(.12+y(2)));
dy(3) = 0.0113*25.55*(y(2)/(.12+y(2))) - 0.6*25.55*(y(3)/(0.16+y(3)));
dy(4)= 0.6*25.55*(y(3)/(0.16+y(3))) - 25.4*25.55*(y(4)/(20+y(4)));
if y(5) > 2*10^(-10)
dy(5)= 25.4*25.55*(y(4)/(20+y(4))) -1.5789*10^(-10)
else
dy(5) = 25.4*25.55*(y(4)/(20+y(4)))
end
if y(5) > 0.0005
if y(6) > 1.6*10^11
dy(6)=0
else
dy(6) = 5*10^6
end
else
dy(6) = 0
end
end
MATLAB output:
The rate at which DCA is removed in solution:
Graph 5: The blue line represents how the concentration of DCA in solution (extracellular) decreases due to the action of our DCA degraders.
The Rate at which the intracellular concentration of the metabolites change over time:
Graph 6: Each line represents the intracellular concentration of each of the metabolites over time within a single cell. The colour associated with each metabolite is depicted in the figure legend. This graph is simply a rescaling of graph 5.
Rescaling the graph once again: the rate at which the metabolic intermediate change over time.
Graph 7: Again, each line represents the intracellular concentration of each of the metabolites over time within a single cell. This graph is simply a rescaling of graph 5 and 6.
The rate at which the cells grow over time:
Graph 8: The blue line represents the linear increase of the total number of cells due to the presence of intracellular glycolate.
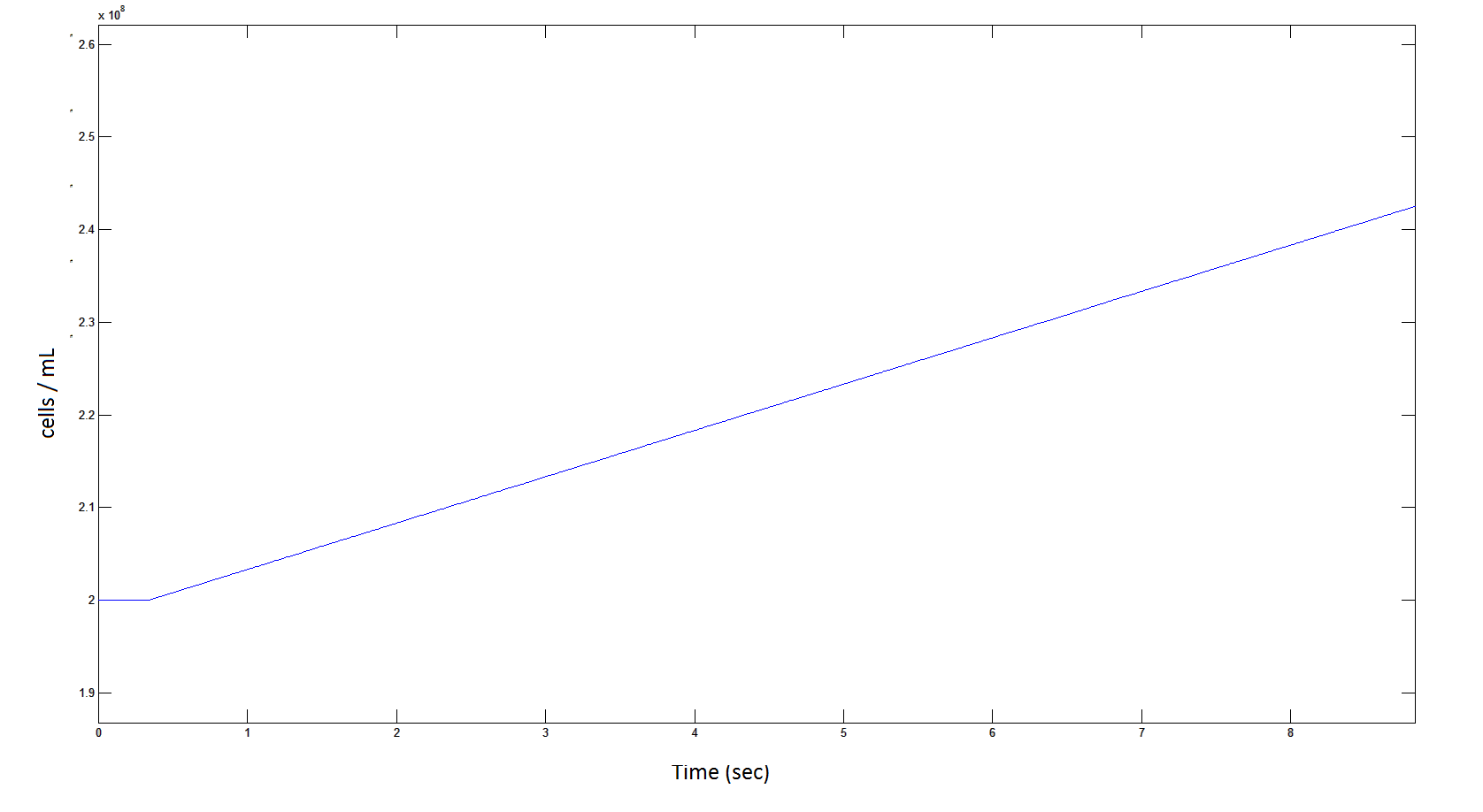
Rescaling Shows a lag effect on cell growth:
Graph 9: The blue line represents the increase of cells due to the presence of intracellular glycolate. This graph is a rescaling of graph 8 to show the inital lag in cellualr growth.
Conclusions:
From Graphs 1 and 5, one can see that 1mM of DCA is removed from solution within roughly 50 minutes when the DCA degrading cells are at a concentration of 2E8 cells/mL.
From Graphs 4, 8 and 9, it is evident that bacterial growth occurs. This growth is due to the production of glycolate, and by comparing graphs 6 and 9, one can see that bacterial growth correlates with glycolate accumulation.
The cytotoxic metabolic intermediate chloroactealdehyde doesn't accumulate to a significant concentration in any of the pathways and is consistently at a negligibly small concentration. From Graphs 3 and 7 one can see that chloroacetaldehyde reaches a maximum concentration of roughly 0.2 mM in both pathways. Chloroacetaldehyde is seen to be metabolised very quickly; this concentration maximum is very short lived where it peaks at roughly 0.03 seconds and returns back to 0 mM by 0.5 seconds. It is expected that chloroacetaldehyde toxicity will not be a problem in our engineered cells.
It is also possible to conclude that the pathways remove DCA at the same rate (through comparing graphs 1 and 5).
References:
[1] Krooshof, G. H., Ridder, I. S., Tepper, A. W., Vos, G. J., Rozeboom, H. J., Kalk, K. H., Dijkstra, B. W. & Janssen, D. B. (1998). Kinetic Analysis and X-ray Structure of Haloalkane Dehalogenase with a Modified Halide-Binding Site. Biochemistry, 37(43), 15013-15023.
[2] Janecki, D. J., Bemis, K. G., Tegeler, T. J., Sanghani, P. C., Zhai, L., Hurley, T. D., Bosron, W. F. & Wang, M. (2007). A multiple reaction monitoring method for absolute quantification of the human liver alcohol dehydrogenase ADH1C1 isoenzyme. Analytical Biochemistry, 369(1), 18-26.
[3] Pandey, A. V. & Flück, C. E. (2013). NADPH P450 oxidoreductase: Structure, function, and pathology of diseases. Pharmacology & Therapeutics, 138(2), 229-254.
[4] van der Ploeg, J., Shmidt, M. P., Landa, A. S., & Janssen, D. B. (1994). Identification of Chloroacetaldehyde Dehydrogenase Involved in 1,2-Dichloroethane Degradation. Applied Environmental Microbiology 60(5), 1599-1605.
[5] van der Ploeg, J., van Hall, G. & Janssen, D. B. (1991) Characterization of the haloacid dehalogenase from Xanthobacter autotrophicus GJ10 and sequencing of the dhlB gene. Journal of Bacteriology, 173(24), 7925-33.
[6] Sinensky, M. I. (1974). Homeoviscous Adaption – A Homeostatic Process that Regulates the Viscosity of Membrane Lipids in Escherichia coli. Proceedings from the National Academy of Science of the United States of America, 71(2), 522-525.
[7] CyberCell Database
[8]
[9]
[10] http://www.dtsc.ca.gov/AssessingRisk/Upload/12dca.pdf
[11] Ishihama, Y., Schmidt, T., Rappsilber, J., Mann, M., Hartl F. U., Kerner, M. J. & Frishman, D. (2008) Protein abundance profiling of the Escherichia coli cytosol. BMC Genomics, 9:102
[12] Lord, J. M. (1972) Glycolate oxidoreductase in Escherichia coli. Biochemica et Biophysica Acta 267:2, 227-327.
 "
"