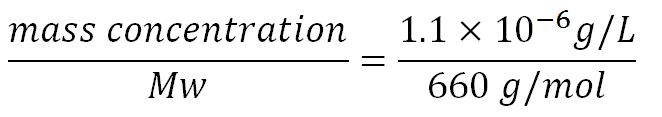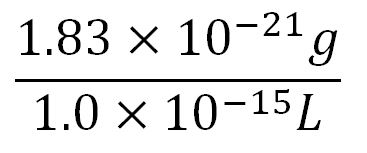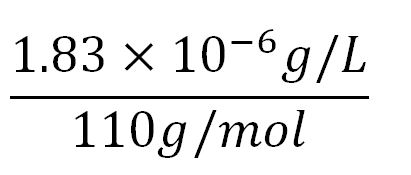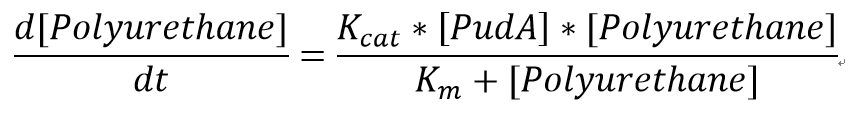Team:Imperial College/Modelling PURdeg
From 2013.igem.org
Contents |
Polyurethane (PUR) Degradation Module
Introduction
Both efficiencies of Polyurethane (PUR) degradation and ethylene glycol production are important for the performance of MAPLE system. We built a mathematical and deterministic model that is based on MATLAB extension Simbiology for Polyurethane degradation. The model contains the kinetic property of degradation enzymes that is helpful for the design of assays. As we scaled up the initial concentrations of all substrates to meet the conditions for a bio-reactor, the model can provide preliminary simulations and predictions for the MAPLE system.
Design
Objective
Here are some specific objectives for the model to achieve:
1. The model should contain the gene expression model of the degradation enzymes because the enzyme concentration determines the rate of plastic degradation. In our case for PUR degradation, we used [http://parts.igem.org/Part:BBa_K206000 pBAD strong promoter K206000] for most enzymes. We built the gene expression model based on inducible pBAD promoter, which gene expression rate can be regulated by inducer concentration.
2. The model should show the efficiency of the enzyme secretion to the culture from the cells. It's also important because the enzyme concentration in the culture depends on it. Here we used pelB secretion tag for most enzymes in order to achieve a high efficiency.
3. The model basically predict how long will take to degrade a known concentration of soluble polyurethane. It is assumed that the enzyme in our assays has the same kinetic properties as the enzyme used in the literature. The model can suggest a suitable concentration of the plastic to use in order to get good results from the assays.
4. It is known that ethylene glycol is toxic to E.coli. However, it has no clear effect on the growth of our MG1655 strain when the concentration of ethylene glycol is below 200mM. Therefore, the model should suggest a safe range of PUR concentration to avoid a high concentration (>200mM) of ethylene glycol produced.
The Model
Polyurethane (PUR) degradation involves 5 different degradation enzymes:
| enzyme | source organism | biobrick | reference |
|---|---|---|---|
| EstCS2 | uncultured unknown bacterium (GU256649.1) | [http://parts.igem.org/Part:BBa_K1149002 BBa_K1149002] | [http://www.microbialcellfactories.com/content/10/1/41 Kang et.al 2011] |
| pueA | Pseudomonas chlororaphis | [http://parts.igem.org/Part:BBa_K1149003 BBa_K1149003] | [http://onlinelibrary.wiley.com/doi/10.1111/j.1574-6968.2000.tb09056.x/pdf Stern et al., 2000] |
| pueB | Pseudomonas chlororaphis | [http://parts.igem.org/Part:BBa_K1149004 BBa_K1149004] | [http://www.sciencedirect.com/science/article/pii/S0964830501000427 Howard et al., 2001] |
| pudA | Comamonas acidovorans | [http://parts.igem.org/Part:BBa_K1149005 BBa_K1149005] | [http://www.sciencedirect.com/science/article/pii/S0964830598000663 Allen et al. 1999] |
| pulA | Pseudomonas fluorescens | [http://parts.igem.org/Part:BBa_K1149006 BBa_K1149006] | [http://www.sciencedirect.com/science/article/pii/S0964830598000687 Vega et al., 1999] |
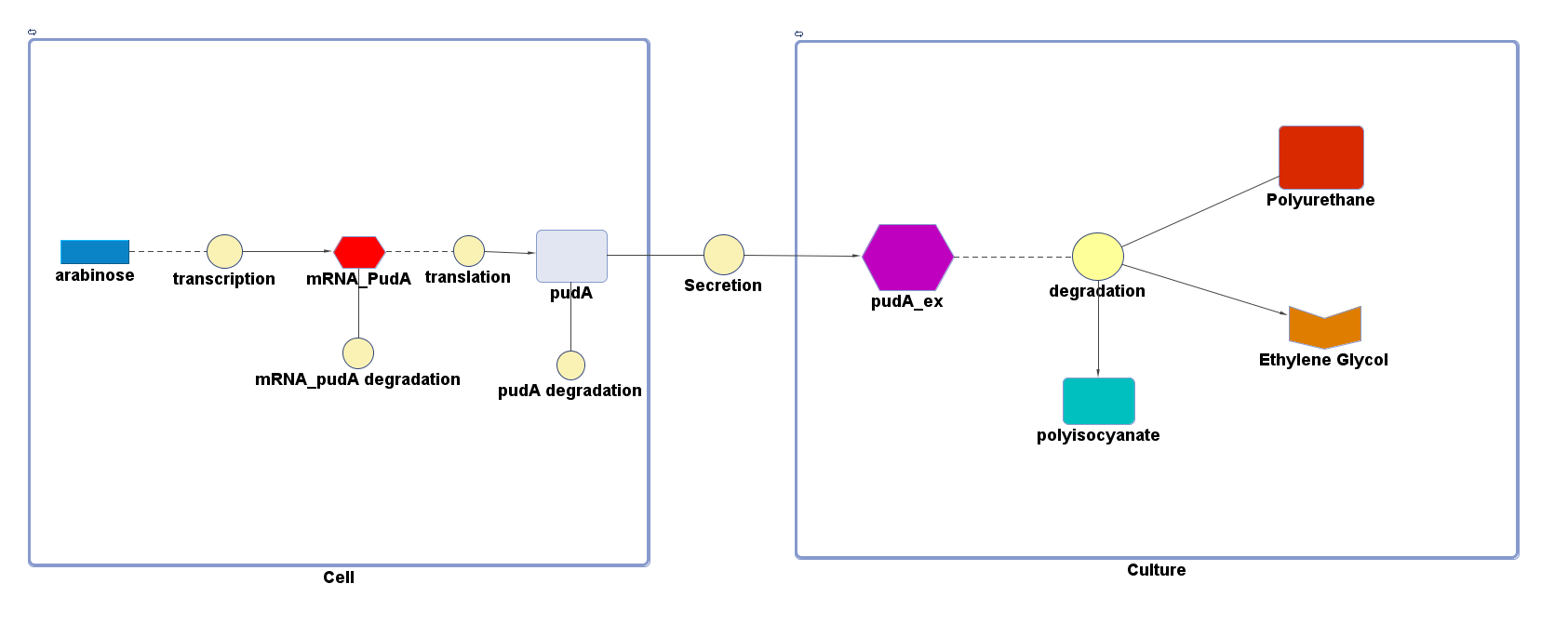
However, 4 of the 5 enzymes are not well characterised before, so we could't find enough kinetic data from the literature. The only well-characterised PUR degradation enzyme PudA is used in the model as an illustration of all PUR degradation enzymes. The model will be more complete when the kinetic data of the other enzymes are defined. The finished PUR degradation model is shown as below:
Key
There are two compartments which represents cells and the culture from left to right. The "cell" compartment contains the gene expression module whereas the "culture" compartment contains the degradation module. The "secretion" block that connects two compartments is the secretion module.
Parameters and assumptions
Gene expression module of PudA
| Parameter | Description | Value | Units | Sources | Assumptions |
|---|---|---|---|---|---|
| β | maximum rate of transcription | 0.032 | mM/min | Please see derivation 1 below. | Please see derivation 1 below. |
| K | Activation coefficient | 0.0031 | mM | [http://parts.igem.org/Part:BBa_K206000:Characterization] | Taking the "switch point" as the activation coefficient |
| dmRNA | mRNA degradation rate | 0.10 | 1/min | [http://www.ncbi.nlm.nih.gov/pmc/articles/PMC420366/pdf/07X.pdf] | Taking the value of mRNA half-life in E.coli strain MG1655 as 6.8min. rate = ln2/half-life = ln2/6.8 = 0.10 |
| dprotein | Protein degradation rate | 0.050 | 1/min | [http://jb.asm.org/content/189/23/8746.full] | There is no active degradation pathway and that dilution is the dominant way by which the protein level decreases in a cell. Rate = 1/doubling time, where doubling time = 20min. Assuming steady-state growth in LB broth as presented in paper. |
| k2 | Protein production rate (PudA) | 4.7 | 1/min | Please see derivation 2 below. | Please see derivation 2 below. |
| [Arabinose] | Concentration of arabinose | Initial: 0.008 | mM | ||
| [mRNA] | Concentration of mRNA | - | mM | - | - |
| [PudA] | Concentration of PudA | - | mM | - | - |
1.Derivation of the maximal expression rate,β
- Average molecular weight (Mw) of a base pair = 660g/mol[http://www.geneinfinity.org/sp/sp_dnaprop.html][http://www.lifetechnologies.com/uk/en/home/references/ambion-tech-support/rna-tools-and-calculators/dna-and-rna-molecular-weights-and-conversions.html]
- Average mass of a base pair = 660g/mol x 1.66x10-24 = 1.1x10-21g
- Volume of an E.coli cell = 1µm3[http://kirschner.med.harvard.edu/files/bionumbers/fundamentalBioNumbersHandout.pdf] = 1x10-15L
- BioBrick assembly plasmid pSB1C3 is a high copy number plasmid (100-300 copies per cell)[http://parts.igem.org/Part:pSB1C3?title=Part:pSB1C3]
- assume 200 copies per cell
- ∴ concentration of the gene per cell = N x 200 x 1.66x10-6mM, where N = number of base pairs
- ∴ concentration of the gene pudA (N = 768) in the volume of an E.coli cell is = 0.25mM
- Transcription rate in E.coli = 80bp/s[http://kirschner.med.harvard.edu/files/bionumbers/fundamentalBioNumbersHandout.pdf] = 80 x 1.66x10-6mM/s = 80 x 1.66x10-6 x 60mM/min = 7.97x10-3mM/min
- ∴ Rate of mRNA_pudA production under the control of pBAD = 7.97x10-3 ÷ 0.25 = 0.032/min
- Average molecular weight(Mw) of an amino acid(aa)= 110g/mol[http://www.genscript.com/conversion.html][http://www.promega.com/~/media/Files/Resources/Technical%20References/Amino%20Acid%20Abbreviations%20and%20Molecular%20Weights.pdf]
- Average mass of an amino acid = 110g/mol x 1.66x10-24=1.83x10-22g/L
- Translation rate = 20aa/s = (20 x 1.66x10-5 x 60)mM/min = 0.020mM/min
- PudA comprises of 256aa[http://www.uniprot.org/uniprot/Q2PEN2&format=html]
- ∴concentration of pudA's aa in the volume of an E.coli = 1.66x10-5mM x 256 = 4.25x10-3mM
- ∴ Rate of protein production = 0.020 ÷ 4.25x10-3 = 4.7/min
PUR degradation module
The reaction equation of the PUR degradation is:
[Polyurethane]+[PudA]= 5 [ethylene glycol] + 5 [polyisocyanate] + [PudA]
Assumptions:
We assumed 1 mole of polyurethane dispersion can produce 5 moles of ethylene glycol.
The molecular weight of a single polyurethane monomer is 470 g/mol whereas the molecular weight of the polyurethane dispersion is around 2000 g/mol.[http://www.polyurethanes.basf.de/pu/solutions/en/content/group/Arbeitsgebiete_und_Produkte/Grundprodukte/Lupraphen-Produktuebersicht_Gewicht]Therefore, the short-chain polyurethane consists approximately 5 monomers. 5 molecules of ethylene glycol will be produced by degrading one chain of polymer.
We also assumed a simple Michaelis-Menten mechanism for PudA
The parameters for the kinetic equations are:
| Parameter | Description | Value | Units | Sources |
|---|---|---|---|---|
| Km | Michaelis constant | 51.5 | mM | [http://www.sciencedirect.com/science/article/pii/S0964830598000663] |
| Kcat | Turnover number | 141.75 | 1/min | [http://www.sciencedirect.com/science/article/pii/S0964830598000663] |
The efficiency of Secretion is assumed to be 90% secretion over 2 hours.[http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1251600/] The rate of secretion in the model is therefore:
rate of secretion = 0.9[concentration of PudA]/120 (mM/mins)
Simulations and Results
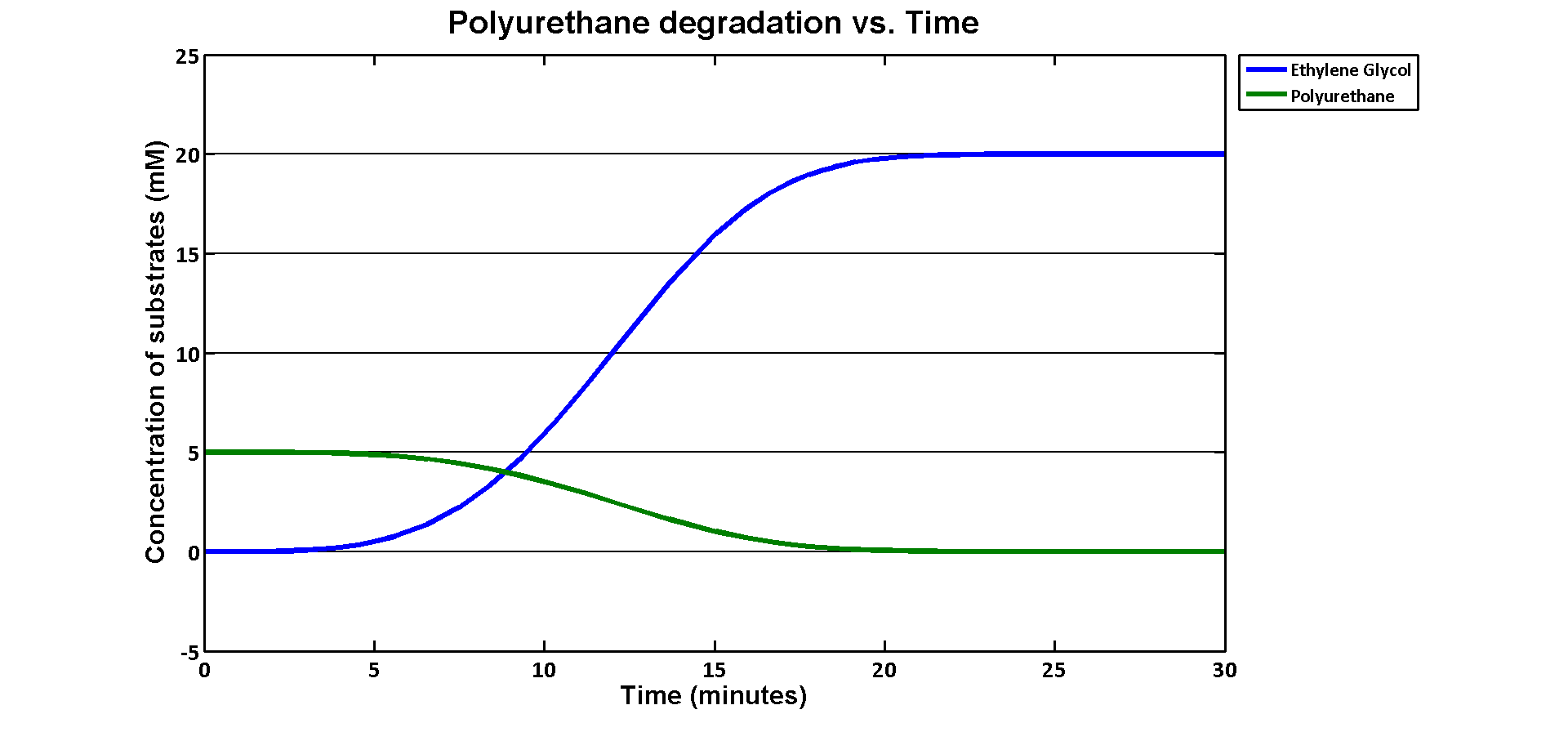
In terms of ethylene glycol toxicity, if we can't let the concentration of ethylene glycol over than 200mM, the maximum initial concentration of polyurethane dispersion is 40mM because one mole of polyurethane dispersion can produce 5 moles of ethylene glycol. (from the derivation above) If we put 40mM as the initial concentration in the model, the simulation result is:
40mM of polyurethane dispersion can be efficiently degraded in 20 mins. In case if we keep the concentration of the plastic below 40mM. The ethylene glycol won't affect the cell growth in our assays. 40mM is converted to 80g/L which suggests no more than 80 grams of polyurethane to be put in the system in order to avoid toxicity.
As for the implementation of MAPLE system, the polyurethane degradation enzymes in our system are very efficient. Therefore, we need an efficient filter which removing ethylene glycol from the system.
 "
"