Team:NYMU-Taipei/Modeling/MainParts

From 2013.igem.org

National Yang Ming University


Contents

Main parts

Backgrounds

Circuit regulators

• ptet regulated promoter (ptet) : when ptet exists, it will bind to ptet regulated promoter (ptet) and represses the promoter.

• pLux/cI hybrid promoter (plux/cI) : when luxR/AHL exists, it will open pLux/cI hybrid promoter (plux/cI), while cI will repress the promoter. What’s more, plux/cI is cI-dominant, which means when cI exists, the hybrid promoter will be repressed whether luxR/AHL exists or not.

Circuit regulation:

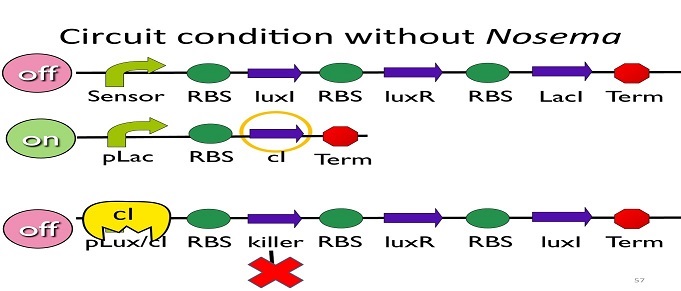
• Circuit condition without Nosema:

NYMU Circuit condition without Nosema.png

Without Nosema ceranae, the first circuit will not open, and thus, no ptet will be produced. Since there is no ptet binding to ptet, ptet will not be repressed, which means cI will be produced. After that, cI will bind to pLux/cI hybrid promoter, leading the third circuit to be off.

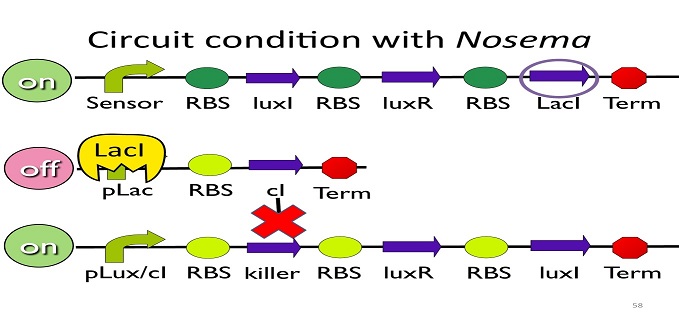
• Circuit condition with Nosema:

NYMU Circuit condition with Nosema.png

When Nosema ceranae infects the bee, bee’s immune system will be activated, leading to the concentration of ROS (reactive oxygen species) to be high. In response, Bee. coli will enhance the production of oxyR, which forms a complex with ROS and binds to transcription binding site ahead of AhpCp (an oxyR-activated promoter; namely, the sensor), leading to the first circuit to be on.

Since the first circuit is on, the downstream ptet gene will be produced and bind to ptet, leading to the second circuit to be off.

After the second circuit is closed, no cI is produced, leading to the third circuit to be on (no repressor at all). And then, kill protein will be produced and kill Nosema Ceranae.

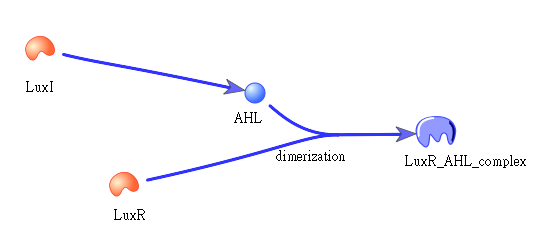
• Positive feedback:

NYMU positive feedback.png

Besides the LuxI and LuxR(which then form a complex called luxR/AHL) produced by first circuit, the third circuit will also produce LuxI and LuxR, which acts as a positive feedback and strongly enhances the production of killer protein.

The picture shows how LuxI will transfer to AHL, which then bind to LuxR to form a dimer:

NYMU luxr ahl dimer.png

• Circuit condition when Nosema is killed:

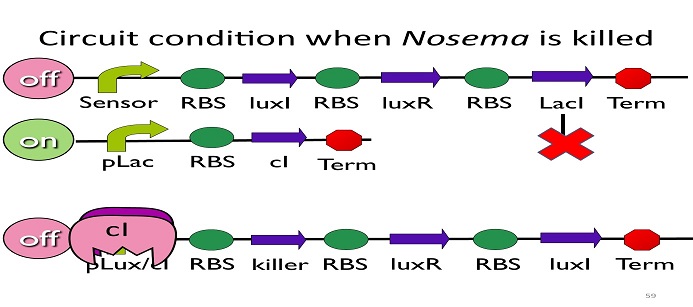
NYMU Circuit condition when Nosema is killed.png

After Nosema is killed, the sensor will be off and no ptet will be produced.

Without ptet, the ptet will not be repressed, and the second circuit will be on, leading to the production of cI. After cI binds to pLux/cI hybrid promoter, the third circuit to be off. After that, the overall circuit will switch to the beginning stage when there is no Nosema.

Objectives

1. To know how much time it needs from sensing to killing the Nosema after infection

2. To know whether the pathway is effective or not

3. To know the range of kill protein concentration (from the minimal concentration which Is effective to kill Nosema to the maximal concentration which will not do harm to the bees)


System

It is assumed that AHL is abundant and thus the formation of AHL2LuxR complex is determined only by the concentration of LuxR; CI’s mechanism of binding to the promoter is assumed to act as hill effect form; kill protein will sustain a period of time before it is degraded naturally without any other types of decomposition.

Equation1

\frac{d[mRNA_C_I]}{dt}= \frac{1-[ptet]^nptet}{ Kdptet^nptet+ [ptet]^nptet} \times PoPSconstitutive\times\frac{N}{V} -KdegmRNA\times [mRNA_C_I]

Kdptet = dissociation constant of CI

nptet = Hill coefficient of ptet

PoPSptet = promoter strength of ptet

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to know mRNA_C_I production rate and when it can reach the level to translate the desired concentration.

read more1

Equation2

\frac{d[mRNA_L_a_c_I]}{dt}= \frac{1-[ROSoxyR]^nROSoxyR }{ KdROSoxyR ^nROSoxyR + [ROSoxyR]^nROSoxyR} PoPSAhpCp\times\frac{N}{V}-KdegmRNA[mRNA_L_a_c_I]

KdROSoxyR = dissociation constant ofROSoxyR

nROSoxyR = Hill coefficient of ROSoxyR

PoPSAhpCp = promoter strength of AhpCp

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to know how AhpCp promoter strength (in PoPS) influences the production of ptet.

read more2

Equation3:

\frac{d[mRNA_O_x_y_R]}{dt}=PoPSconstitutive\times\frac{N}{V}-KdegmRNA\times [mRNAOxyR]

PoPSconstitutive= promoter strength of constitutive promoter (J23102)

N = number of plasmid in a single cell

V = volume of a cell

kdegmRNA = degrading constant of sensor promoter mRNA

The aim of the equation is to know the production rate ofmRNAoxyR, and choose the proper constitutive promoter for boosting OxyR's concentration.

read more3

Equation4:

\frac{d[mRNA_L_u_x_I]}{dt}= \frac{1-[ROSoxyR]^n ROSoxyR }{ Kd ROSoxyR ^n ROSoxyR + [ROSoxyR]^n ROSoxyR I} PoPSAhpCp\times\frac{N}{V}+\frac{1-[ LuxRAHL]^nLuxRAHL}{ KdLuxRAHL ^nLuxRAHL + [LuxRAHL]^nLuxRAHL}\times\frac{1-{1-[CI leak]^nCI}}{ KdCI^nCI+[CI]^nCI}\times PoPSLuxCI\times\frac{N}{V}-KdegmRNA[mRNALuxI]

KdROSoxyR = dissociation constant ofROSoxyR

nROSoxyR = Hill coefficient of ROSoxyR

PoPSAhpCp = promoter strength of AhpCp

KdLuxRAHL = dissociation constant ofLuxRAHL

nLuxRAHL = Hill coefficient of LuxRAHL

KdcI = dissociation constant of CI

ncI = Hill coefficient of CI

PoPSLuxcI = promoter strength of LuxcI hybrid promoter

kdegmRNA = degrading constant of sensor promoter Mrna

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to know how AhpCp promoter strength (in PoPS) influences the production of LuxI.

read more4

Equation5:

\frac{d[mRNA_L_u_x_R]}{dt}= \frac{1-[ROSoxyR]^n ROSoxyR }{ Kd ROSoxyR ^n ROSoxyR + [ROSoxyR]^n ROSoxyR I} \times PoPSAhpCp\times\frac{N}{V}+\frac{1-[ LuxRAHL]^nLuxRAHL}{ KdLuxRAHL ^nLuxRAHL + [LuxRAHL]^nLuxRAHL}\times\frac{1-{1-[CI leak]^nCI}}{ KdCI^nCI+[CI]^nCI}\times PoPSLuxCI\times\frac{N}{V}-KdegmRNA[mRNALuxR]

KdROSoxyR = dissociation constant ofROSoxyR

nROSoxyR = Hill coefficient of ROSoxyR

PoPSAhpCp = promoter strength of AhpCp

KdLuxRAHL = dissociation constant ofLuxRAHL

nLuxRAHL = Hill coefficient of LuxRAHL

KdcI = dissociation constant of CI

ncI = Hill coefficient of CI

PoPSLuxcI = promoter strength of LuxcI hybrid promoter

kdegmRNA = degrading constant of sensor promoter Mrna

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to know how AhpCp promoter strength (in PoPS) influences the production of LuxR.

read more5

Equation6

\frac{d[mRNA_k_i_l_l]}{dt}= \frac{1-[ LuxRAHL]^nLuxRAHL}{ KdLuxRAHL ^nLuxRAHL + [LuxRAHL]^nLuxRAHL}\times\frac{1-{1-[CI leak]^nCI}}{ KdCI^nCI+[CI]^nCI}\times PoPSLuxCI\times\frac{N}{V}-KdegmRNA[mRNA_k_i_l_l]

KdLuxRAHL = dissociation constant ofLuxRAHL

nLuxRAHL = Hill coefficient of LuxRAHL

KdcI = dissociation constant of CI

ncI = Hill coefficient of CI

PoPSLuxcI = promoter strength of LuxcI hybrid promoter

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to know mRNA of kill protein production rate and when it can reach the level of the desired concentration.

read more6

to learn more about how we characterize pLuxCI, click here


Equation7

\frac{d[mRNA_t_7]}{dt}= \frac{1-[ROSoxyR]^n ROSoxyR }{ Kd ROSoxyR ^n ROSoxyR + [ROSoxyR]^nROSoxyR }\timesPoPSAhpCp\times\frac{N}{V}\times {a}+ \frac{1-[T7]^nT7}{ Kd T7^nT7 + [T7]^nT7}\times{PoPST7}\times\ frac{N}{V}-KdegmRNA\times [mRNA_T_7]

KdROSoxyR = dissociation constant ofROSoxyR

nROSoxyR = Hill coefficient of ROSoxyR

PoPSAhpCp = promoter strength of AhpCp

KdT7 = dissociation constant of T7

NT7 = Hill coefficient of T7

PoPST7 = promoter strength of T7 promoter

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to know mRNA of T7 polymerase production rate and when it can reach the level to translate enough T7 polymerase.

read more7

Equation8:

\frac{d[mRNA_P_D_C]}{dt}=\frac{ [T7]^{nT7} }{ KdT7^{nT7}+[T7]^{nY7} }\times{PoPST7}\times\frac{N}{V}-KdegmRNA\times[mRNAPDC]

KdT7 = dissociation constant of T7

NT7 = Hill coefficient of T7

PoPST7 = promoter strength of T7 promoter

KdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to knowmRNA of enzyme PDC production rate and when it can reach the level to translate enough PDC.

read more8

Equation9:

\frac{d[mRNA_A_D_H]}{dt}=\frac{ [T7]^{nT7} }{ KdT7^{nT7}+[T7]^{nY7} }\times{PoPST7}\times\frac{N}{V}-KdegmRNA\times[mRNAADH]

KdT7 = dissociation constant of T7

NT7 = Hill coefficient of T7

PoPST7 = promoter strength of T7 promoter

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to knowmRNA of enzyme ADH production rate and when it can reach the level to translate enough ADH.

read more9


Equation10

\frac{d[CI]}{dt}={RBS}\times{[mRNA_C_I]} -KdegCI\times{[CI]}

RBS = binding site strength

KdegCI = degrading constant of CI

The aim of the equation is to know the production rate of CI and when it can reach the concentration to repress LuxCI hybrid promoter.

read more10

Equation11

\frac{d[ptet]}{dt}={RBS}\times{[mRNA_L_a_c_I]} - {Kdeg ptet} \times{[ptet]}

RBS = binding site strength

Kdegptet = degrading constant of ptet

The aim of the equation is to known ptet production rate and when it can reach the concentration to repress promoter ptet.

read more11

'Equation12

\frac{d[LuxI]}{dt}={RBS}\times{[mRNA_L_u_x_I]} -KAHL\times{[LuxI]} -Kdeg {[LuxI]} \times{[LuxI]}

RBS = binding site strength

KAHL = LuxI to AHL rate constant

KdegLuxI = degrading constant of LuxI

The aim of the equation is to know the production rate of LuxI concerning the LuxIAHL reaction and LuxI degrading.

read more12

'Equation13

\frac{d[LuxR]}{dt}={RBS}\times{[mRNA_L_u_x_R]} – {KmAHL}\times{[AHL]} - {Kdeg LuxR} \times{[LuxR]} \times {KmAHL}\{times[AHL]^{2}} \times{[LuxR]}- KdegAHL\times{[AHL]}

RBS = binding site strength

KmAHL =AHL to LuxI rate constant

KdegLuxR= degrading constant of LuxR

KonAHL = 2AHL + LuxR to (AHL)2/LuxR complex rate constant

KdegAHL = degrading constant of AHL

The aim of the equation is to know the production rate of LuxR concerning the 2AHL + LuxR to (AHL)2/LuxR reaction , AHL to LuxI reaction, and LuxR, AHL degrading.

read more13

'Equation14:

\frac{d[AHL]}{dt}={KAHL}\times{[LuxI]}+2\times KoffAHL \times [AHLLuxR] - 2\times KonAHL \times {[AHL]}^{2}\times {[LuxR]} - KdegAHL\times{[AHL]}

KAHL = LuxI to AHL rate constant

KonAHL = 2AHL + LuxR to (AHL)^2/LuxR complex rate constant

KoffAHL = (AHL)2/LuxR complex to 2AHL + LuxR rate constant

KdegAHL = degrading constant of AHL

The aim of the equation is to know the production rate of AHL concerning the LuxIAHL reaction, 2AHL + LuxR to (AHL)2/LuxR reaction, (AHL)2/LuxR complex to 2AHL + LuxR reaction and AHL degrading.

read more14


Equation17

\frac{d[ADH]}{dt}=RBS\times{PoPST7effect}\times\frac{N}{V}-{KdegADH}\times{[ADH]}


RBS = binding site strength

PoPST7 = promoter strength of T7 promoter

N = number of plasmid in a single cell

V = volume of a cell

KdegADH = degrading constant of ADH (Acetaldehyde)

The aim of the equation is to know ADH production rate and when it can reach the concentration of ethanol pathway equilibrium.

read more17

Equation18

\frac{d[AHL]}{dt}=\times KonAHL \times [AHL]^{2}\times{[LuxR]}- {KoffAHL} \times {[AHLLuxR]} - KdegAHL\times{[AHL]}

KAHL = LuxI to AHL rate constant

KonAHL = 2AHL + LuxR to (AHL)2/LuxR complex rate constant

KoffAHL = (AHL)2/LuxR complex to 2AHL + LuxR rate constant

KdegAHL = degrading constant of AHL

The aim of the equation is to know the production rate of AHL concerning the LuxIAHL reaction, 2AHL + LuxR to (AHL)2/LuxR reaction, (AHL)2/LuxR complex to 2AHL + LuxR reaction and AHL degrading.

read more18

Equation19

\frac{d[kill]}{dt}={RBS}\times{[mRNA_k_i_l_l]} –Kdegkill\times{[kill]}

RBS = binding site strength

Kdegkill = degrading constant of kill

The aim of the equation is to knowkiller protein production rate and when it can reach the effective concentration to kill Nosema.

read more19


Results

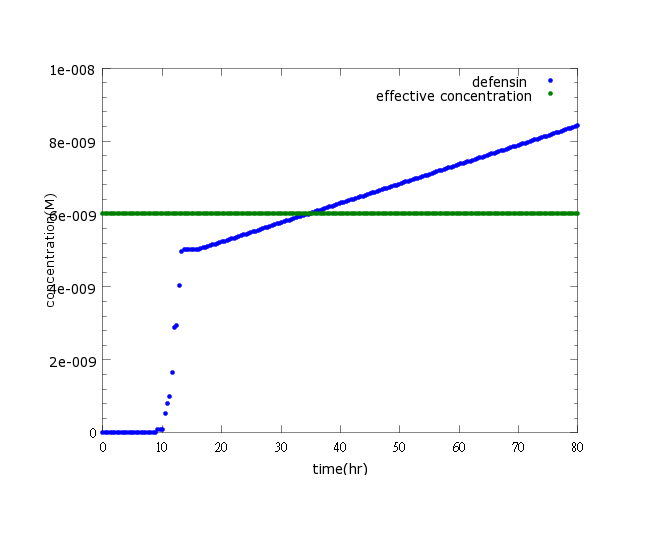
NYMU defensin normal.png

Figure1: This picture shows kill protein concentration to time under pLux/CI hybrid promoter’s control and LuxR, LuxI’s positive feedback. The result indicates that kill protein concentration will reach its effective level and kill Nosema in time (36 hours after Nosema infection)

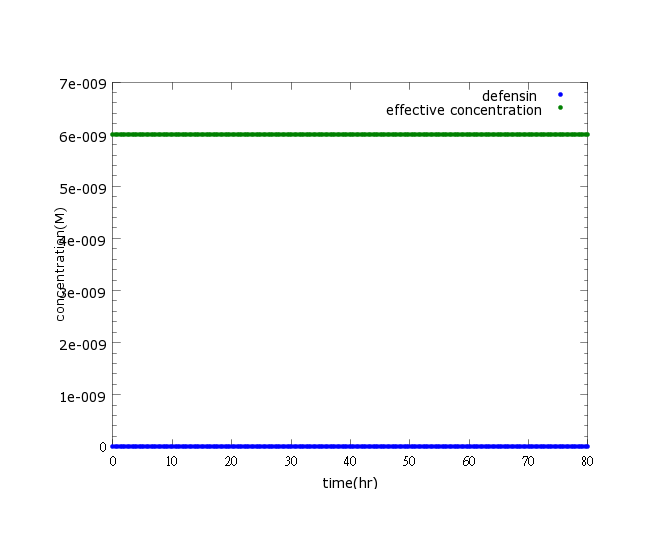
NYMU defensin witout ROS.png

Figure2: This picture is a control group model. It shows that without Nosema infection (ROS concentration=0), ethanol production is low enough to be ignored.

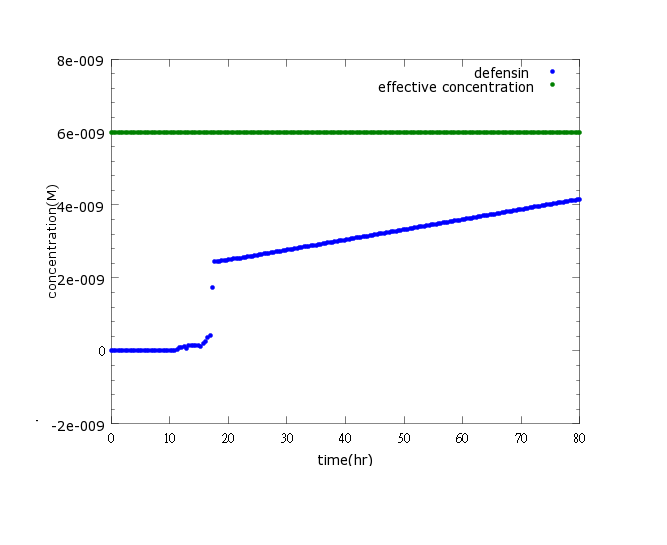
NYMU defensin only CI.png

Figure3: This is the picture of kill protein concentration to time under promoter CI’s control only(control group)without pLux/CI's regulation.The result shows that kill protein's full expression is too low to kill Nosema.

Discussion

Comparing to the ROS-level control group where ROS remains low when there’s no Nosema infection, kill protein production is highly boasted upon sensing Nosema.

The result indicates that kill protein concentration will reach its effective level and kill Nosema in time (36 hours after sensing Nosema infection, within the 5-day deadline when Nosema spores proliferates and the bee become incurable and infectious to other bees), at the given ROS changes and the enhanced OxyR expression (to learn more about our sensor model, click here).

Circuit design and improvement

Upon using pCI to negatively regulate kill protein production, results show that kill protein's full expression while no CI present is too low to kill Nosema. To solve this problem we subsidized CI promoter into pLux/CI promoter for additional positive feedback to boast kill protein’s production. As the modeling results regarding the modified circuit shown, the consequences are positive. (click here to learn more about our circuit)

Parameters:

Model Parameter Description Value Unit Reference
Sensor KdegOxyR OxyR degrading rate 107 M-1 x min-1 Regulation of the OxyR transcription factor by hydrogen peroxide and the cellular thiol—disulfide status
KdOxyR* Dissociation constant of OxyR* 10-7.33 M
KOxyR OxyR producing rate constant 5.012 x 1014 X
nOxyR* Hill coefficient of OxyR* Ranging from 0.75~3.5,depends on what kind of ROS it react with X OxyR: A Molecular Code for Redox-Related Signaling
N Copy number 887(cells containing 25％ plasmid bearing cells) Single piece
  1. Escherichia coli Plasmid Copy Number Assay
  2. Improved determination of plasmid copy number using quantitative real-time PCR for monitoring fermentation processes
Ethanol


pyruvate Initial concentration of pyruvate in MG1655 1.18 x 2 g/L Expression of pyruvate carboxylase enhances succinate production in Escherichia coli without affecting glucose uptake
nPDC Hill coefficient of PDC 2.1 - Purification, characterization and cDNA sequencing of pyruvate decarboxylase Zygosaccharomyces biporus
nADHHill coefficient of ADHat high pH values, 30◦C, n=1; at low temperature, n=3 - Evidence for co-operativity in coenzyme binding to tetrameric Sulfolobus

solfataricus alcohol dehydrogenase and its structural basis: fluorescence, kinetic and structural studies of the wild-type enzyme and non-co-operative N249Y mutant

SEIR(exponential)


b Infection rate constant of Nosema ceranae to the suspected 24/75 Period(days)-1
r1 Infection rate constant of K12 to the suspected 3/20 Period(days)-1 1. Environment protection administration executive yuan of R.O.C Medical bacteriology of J.A.T
r2Infection rate constant of K12 to the latent3/20 Period(days)-1 2. Environment protection administration executive yuan of R.O.C.
3. Medical bacteriology of J.A.T
e rate of the latent turns infectious1/4Period(days)-1
u Death rate of the infected 1/8Period(days)-1
k Rate of intaking capsule 24/11Period(days)-1
SEIR(exponential&linear) S x(1) Amount of total population
E x(2) Amount of suspected individuals
Ix(3)Amount of individuals in the latent period
R x(4)Amount of infected individuals

Retrieved from "http://2013.igem.org/Team:NYMU-Taipei/Modeling/MainParts"