Team:Paris Bettencourt/Project/Sabotage/Model
From 2013.igem.org


Introduction
Synthetic biology relies on the addition of foreign genetic elements into organisms for their manipulation. This has the advantage to introduce orthogolous systems, avoiding many unwanted interactions with the organism's own processes (Guttinger 2013). However, every introduced system will consume cell's resources and compete for the molecular machinery responsible of replication (DNA level), transcription (RNA level), and translation (protein level). In case the device provides no direct benefit for the organism, the burden of the device will lead to a decrease in growth rate, and therefore a lower fitness (Shachrai et al. 2010).
One way to avoid out-competition due to lower growth rate is by horizontal gene-transfer. Here we will study the behavior of a the phagemid/helpel system, which is a derived from from the non-lytic bacteriophage M13. This systems propagate through E. coli F+ populations via two vectors: a phagemid carrying the desired device, and a helper carrying the necessary machinery for production of the bacteriophage. Only when both vectors are present in a cell it will produce bacteriophage (see figure 1 below). Furthermore the system is designed such that the phagemid is produced in higher abundance than the helper.
We took the M13 infection model of (Wan et al. 2012) as a reference, and adapted to the phagemid/helper system. For the burden of protein expression we used the results from Shachrai et al. (2010) as a reference.
Notation: through this document we will use capital letter to denote cell populations, lower case to denote phagemid populations, and greek letters to denote functions and parameters.
Deterministic Model
Cell populations can growth up to a maximum concentration that depends on the media, called carrying capacity (κc). Furthermore cells share the resources used for growth (S). Here following classic work in bacterial population dynamics we have chosen to represent bacterial growth as a logistic function (λ) together with an asymptotic dependency on the substrate concentration (β), commonly known as Monod's equation.
As we are interested in a chemostat-like system, all elements in the system will be subject to dilution due to eflow of media (with rate constant γ). Any other decay will be assumed to be negligible compared to eflow dilution. The addition of new media carrying substrate is coupled to the chemostat flow. The concentration of substrate added to the media is δ. To the right you can see the equations for n cell types (C)
Infection was assumed to follow mass action kinetics. This implies that the rate of infection is proportional to the phagemid (p) and a recipient cell (R). However, we need to account for the fact that M13 derived phagemid rely on the expression of the F-pili for infection, which is known to be less likely to be absent when resources are limited. For that, we have included the saturation function from Monod's equation into the infection rate. For simplification, we will assume that cells can get infected only by one phagemid. It is known that M13 infection inhibits the expresion of F-pili citep{Lin2011}.
M13 is a non-lytic phage, meaning that cells infected produce new phages without the need of lysing the cell. We will neglect any killing of cells due to infection. We will assume that cells have a delay in producing phages (F → F*) with constant rate τ. Then F* produce phages with constant maximal rate φ, which is modulated by the substrate concentration (β(S)). Finally, we know that phagemids are more likely to be produced that the helper. We called the ratio of production ψ.
Finally we have the following ODE describing the dynamics of our system.

The equations for M13 alone model are easy to infer by changing the number of infective elements and cells populations. More details please refer to the supplied Matlab scripts.

where θ is the concentration of substrate of half saturation, and κ is the carrying capacity.

where 1-α represents the relative reduction in maximal growth rate.

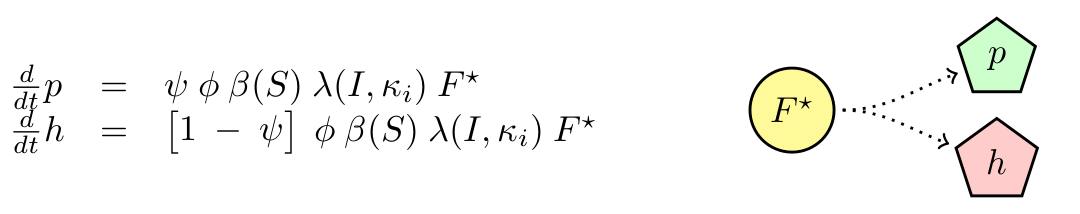

Figure 1:
| Variable | Description |
|---|---|
| R | Recipient (cells/ml) |
| P | Phagemid infected (cells/ml) |
| H | Helper infected (cells/ml) |
| F | Phagemid+helper infected inactive (cells/ml) |
| F* | Phagemid+helper infected active (cells/ml) |
| p | Phagemid (phages/ml) |
| h | Helper (phages/ml) |
| S | Substrate (a.u./ml) |
All deterministic simulations where done in Matlab together with the library ODEMEXv12 for numerical inegration. Scrips can be found here. Unless stated otherwise parameters are as described on the table in the right.
| Parameter | Units | Value | Source |
|---|---|---|---|
| μ | h-1 | 2.1 | Wan et al. 2012 |
| αp | 0.99 | Shachrai et al. 2010 | |
| αh | 0.6 | Assumed | |
| αf | 0.6 | Wan et al. 2012 | |
| κc | cells ml-1 | 3e09 | Wan et al. 2012 |
| θ | a.u. ml-1 | 1 | Wan et al. 2012 |
| δ | a.u. ml-1 | 200 | Wan et al. 2012 |
| ν | a.u. cells-1 | 3.5e-08 | Wan et al. 2012 |
| κi | phages ml-1 | 2e11 | Lin et al. 2011 |
| τ | h-1 | 2 | Wan et al. 2012 |
| ι | ml phages-1 | 1e-08 | Lin et al. 2011 |
| φ | phages cells-1 h-1 | 60 | Lin et al. 2011 |
| ψ | 0.9 | Assumed | |
| γ | h-1 | 0.1 | Hypothetical |
Results
Given the parameters we collected from the literature, we found that given some initial concentration of recipient cells, there is always some concentration of phage that leads to the prevalence of the factory cells (F*). For example, figure 2 show simulations with 105 R and 106 for each phage. The time scale of our model is dominated by the dilution rate (γ), as it control the time scale at which the substrate is replaced and the rate at which cells are diluted. The higher it is, the fastest the transition from recipients to factory cells will take place. Given the nature of the equations, this dependency is exponential. This dependency is higher for the phagemid/helper system than the original M13, as we have more cell types and we need two infection events to reach the factory cells.
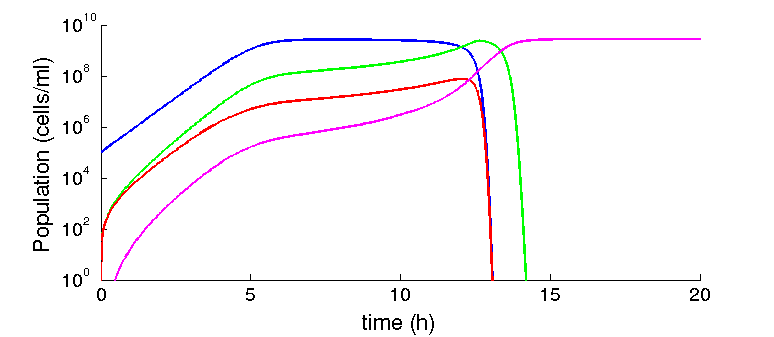

Figure 2: Infected cells dominate the population
Effect of fitness cost
At the beginning of our project, we found a strong effect of the phagemid fitness on the spreading on the population. However, after finding experimentally derived parameters we found that our assumptions were different from the natural system. We worked with costs of over 20% for the phagemid, and production rates way lower. Given our parameters, and a range of cost from 0-10% we find no effect on the steady state: the factory will eventually dominate the population. However, if the production rate is reduced in one order of magnitude (from 60 phages per cell to 6.5 phages per cell), a difference in 1% (from 99% to 98%) is enough to make the spreading of the system unstable (see figure 3).

Figure 3: Al lower production rates, low differences in fitness matters
Stochastic Model
We attempted to convert our deterministic model into stochastic using the rule-based language Kappa. We think that inside the lungs phenomena relating few number of cells are relevant. We believe agent-based abstractions can be useful to represent the distinct states of cell populations, and indeed our system is reduced to a few core rules. In principle it could be easily adapted to include as many infective elements as wanted with little modification to the core rules
We are working now on fixing the conversion of the equations to discrete space, as some of our function are macroscopic and do not have an intuitive translation. In principle parameters should be normalized by volume, and bi-molecular reaction should be divided by the volume. Files can be downloaded here

Figure 4: Sample stochastic trajectory
References
- Stephan Guttinger (2013).Creating parts that allow for rational design: Synthetic biology and the problem of context-sensitivity. Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences. 44:199-207.
- Irit Shachrai, Alon Zaslaver, Uri Alon, and Erez Dekel (2010). Cost of Unneeded Proteins in E. coli Is Reduced after Several Generations in Exponential Growth. Molecular Cell, 38:758-767.
- Wan, Zhenmao and Goddard, Noel L. (2012). Competition Between Conjugation and M13 Phage Infection in Escherichia coli in the Absence of Selection Pressure: A Kinetic Study. G3: Genes|Genomes|Genetics2:1137-1144.
- Lin, Abraham et al. (2011). Inhibition of Bacterial Conjugation by Phage M13 and Its Protein g3p: Quantitative Analysis and Model .PLoS ONE, 6:e19991.
 "
"







 +33 1 44 41 25 22/25
+33 1 44 41 25 22/25


