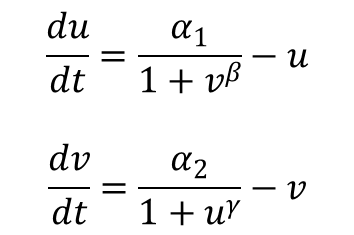Mathematical Modeling of Bistable Toggle Switch

Kinetic Model of Bistable System

Following Gardner's Work...

Tim Gardner from Jim Collins' Lab of Boston Univeristy published one of the first major papers on genetic toggle switch. In his work, he used a kinetic approach to model the stability of a genetic toggle switch. His equations involved two equations expressing the change in the level of two mutually repressive repressors with respect to time.

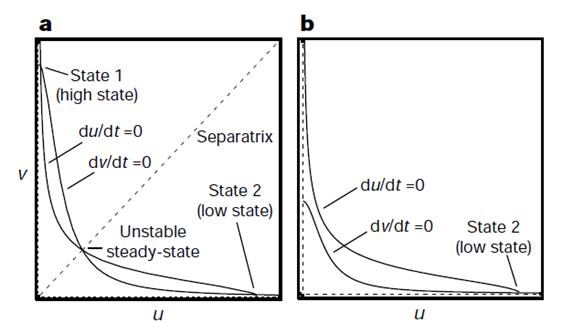
Using this model, Gardner produced the two graphs shown below. The first is a graph of nullclines. Nullcline, also called zero-growth isocline, is a line that represents the set of points at which the rate of change is zero. In this example, the two nullclines shown are where rate of change of repressor 1 (U) and repressor 2 (V) are zero. It is clear that at the intersection of these two nullclines are steady-state points of the system because these are points where the change of both repressor levels with respect to time is zero.

The difference between the two figures with nullclines on left and right is that the system on the left is bistable with the system on the right is mono-stable. Figure (a) shows that there are two stable steady-states where only one of the two repressors exists at a high level, inhibiting the production of the other repressor. There exists a third intersection in the middle, however, this point can be mathematically shown to be unstable using the eigenvalue of the Jacobian matrix involving U and V (workings not included here). The value of U and V doesnt change exactly at this unstable steady-state, however, the level of repressors will quickly diverge from this point even at the smallest perturbation. The figure on the right, figure (b), shows that at a different combination of parameters, a system can be mono-stable where the nullclines only intersect once at a stable steady-state solution.

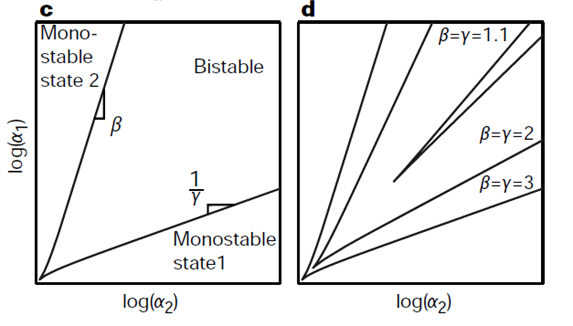
Another set of graphs from Gardner's work is shown below. The two plots are bifurcation diagrams of a system, again, with two mutually repressive genes. Bifurcation is a mathematical term that describes a phenomena "when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior" (Blanchard). In terms of this system in question, bifurcation occurs when the system changes its stability (Change between monostability and bistability).

The graphs below shows the effect of change in cooperativity on the bifurcation region. On the two axes are rate of synthesis of the two repressors, which can be translated as the strengths of the two promoters. According to the graphs, the bifurcation increases as cooperativity increases. In other words, increasing cooperativity of mutual repression allows a set of two weaker promoters to have bistability.

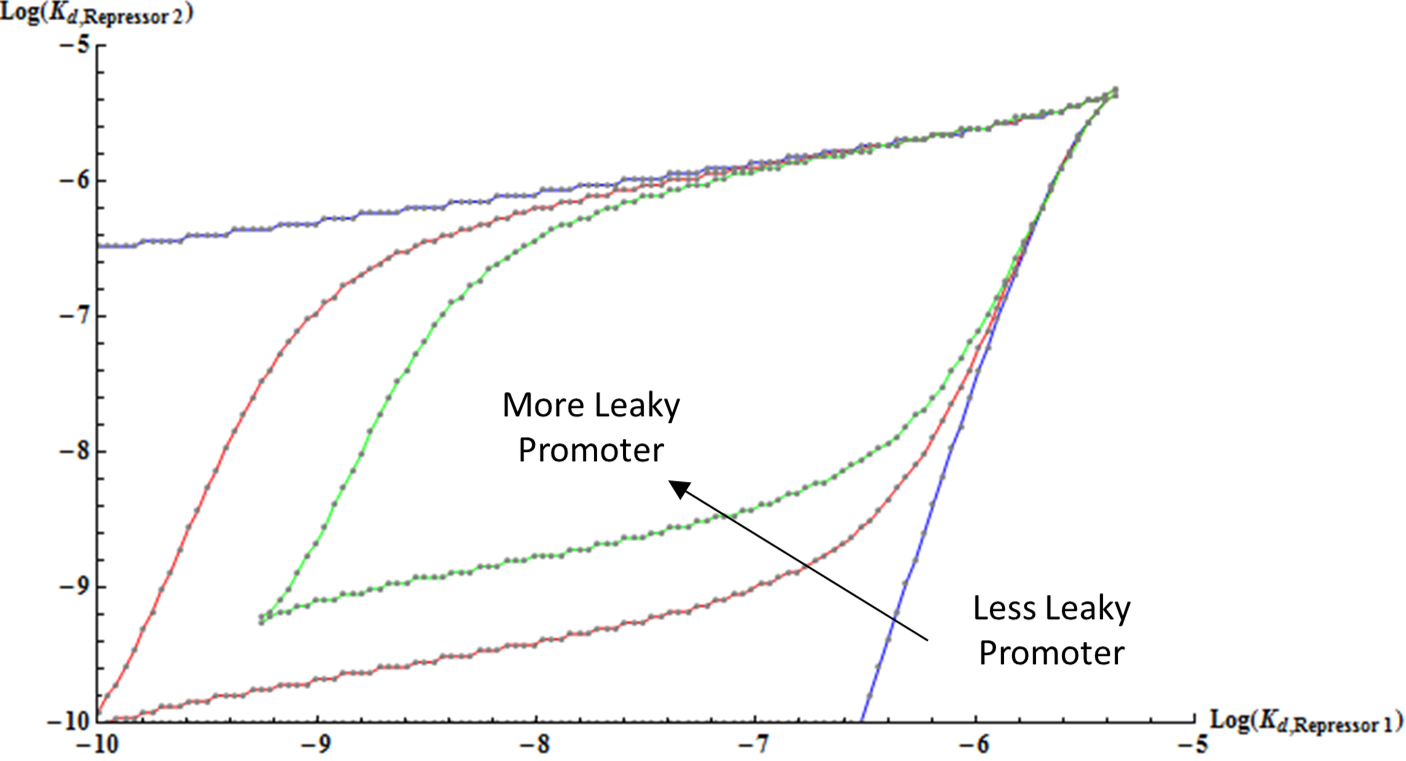
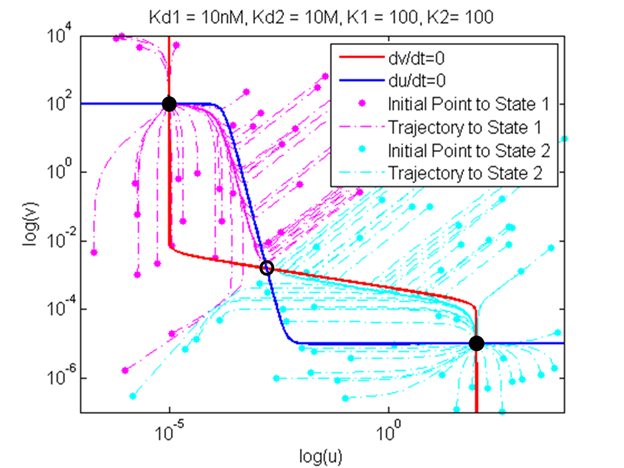
Following his work, I have generated plots that show nullclines of two repressors for various combinations of the parameters alpha1, alpha2, beta, and gamma (which is equivalent to a1, a2, n1, n2 in the plots below). In addition to the nullclines, the plots show the trajectories of how points with different initial conditions on the level of U and V end up at either of the two stable steady states. All the trajectories are color-coded in terms of where they eventually end up--the line across the middle labeled as "separatrix" separates the initial conditions that lead to one solution from the initial conditions that lead to the other solution. Two interesting observations can be made. First, some trajectories reach close to the unstable-steady state but when it gets very close to it, it quickly diverges to either of the two stable steady-state solutions. Secondly, the plot on the right shows that when the set of promoters are chosen appropriately, the system becomes monostable and all initial points end up at the single stable steady-state solution.

Development of Our Kinetic Model

With the understanding of bifurcation regions and their meaning on a system of two mutually repressive genes, we have created our own kinetic model with the purpose of exploring the conditions necessary for a system to be bistable. Our model shown below incorporates the P_bound term from our thermodynamic model. In this sense, this model is a combination of kinetic and thermodynamic model. As mentioned before, a key assumption in this model is that the gene expression is directly proportional to the probability of RNAP bound to the promoter.

gardner = effect of hill coeff on bistability of a system (bifurcation region) new model = effect of various parameters on bistability (highlight and number Kd, pr_Str, basal rate.

explain

show values for variables like degradation rate

Results from Our Kinetic Model

show graph

explain

show nullcline

confirm bistability of the system (thermodynamic model incorporated into kinetic model)

References

1. Gardener, T. et al. Construction of a genetic toggle switch in Escherichia coli. Nature. 403, 339-342 (2000).
2. Blanchard, P.; Devaney, R. L.; Hall, G. R. (2006). Differential Equations. London: Thompson. pp. 96–111.