Team:Evry/Modeltr2
From 2013.igem.org
| (6 intermediate revisions not shown) | |||
| Line 18: | Line 18: | ||
</p> | </p> | ||
| - | <h2> | + | <h2>Goal</h2> |
<p> | <p> | ||
This model was made to check if our first strategy was viable. It aims to answer the following question: <br/> | This model was made to check if our first strategy was viable. It aims to answer the following question: <br/> | ||
| Line 51: | Line 51: | ||
<img src="https://static.igem.org/mediawiki/2013/1/1b/Duoeqcoul.png" width=300px /><br/> | <img src="https://static.igem.org/mediawiki/2013/1/1b/Duoeqcoul.png" width=300px /><br/> | ||
<p> | <p> | ||
| + | |||
| + | <br/> | ||
| + | <table border="1" style="border-collapse:collapse;"> | ||
| + | <tr> | ||
| + | <td><b>S<sub>p</sub></b></td> | ||
| + | <td>mol.s<sup>-1</sup></td> | ||
| + | <td>Iron pulse</td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td><b>v</b></td> | ||
| + | <td>m.s<sup>-1</sup></td> | ||
| + | <td>Chyme's flow average speed</td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td><b>L</b></td> | ||
| + | <td>m</td> | ||
| + | <td>Duodenum length</td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td><b>α</b></td> | ||
| + | <td>s<sup>-1</sup></td> | ||
| + | <td>Duodenum absorption rate</td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td><b>K</b></td> | ||
| + | <td>mol/s</td> | ||
| + | <td>Activator Magnitude</td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td><b>p</b></td> | ||
| + | <td>mol.s<sup>-1</sup></td> | ||
| + | <td>Value at zero of the activator</td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td><b>h</b></td> | ||
| + | <td>-</td> | ||
| + | <td>Activator efficiency</td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td><b>d</b></td> | ||
| + | <td>mol</td> | ||
| + | <td>Activator threshold</td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td><b>δ</b></td> | ||
| + | <td>mol<sup>-1</sup></td> | ||
| + | <td>Chelation rate</td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | <br/><br/> | ||
The graph on the right explains the reasoning: for instance, the arrow with a + between N and P means that the variation of P has a positive linear term in N. | The graph on the right explains the reasoning: for instance, the arrow with a + between N and P means that the variation of P has a positive linear term in N. | ||
</p> | </p> | ||
| Line 163: | Line 213: | ||
<td>2.65*10<sup>-8</sup></td> | <td>2.65*10<sup>-8</sup></td> | ||
<td>mol<sup>-1</sup></td> | <td>mol<sup>-1</sup></td> | ||
| - | <td> | + | <td>Chelation rate</td> |
<td><a href="#Ref">[4]</a></td> | <td><a href="#Ref">[4]</a></td> | ||
</tr> | </tr> | ||
| Line 178: | Line 228: | ||
<h2>Models and scripts</h2> | <h2>Models and scripts</h2> | ||
<p> | <p> | ||
| - | This model was made using the Python language. You can <a href="https://static.igem.org/mediawiki/2013/ | + | This model was made using the Python language. You can <a href="https://static.igem.org/mediawiki/2013/a/ae/Duodenummodel.zip"> download the python script here</a>. |
</p> | </p> | ||
| Line 187: | Line 237: | ||
<li>Physiol Rev 93: 1721–1741, 2013 doi:10.1152/physrev.00008.2013 - Tomas Ganz "SYSTEMIC IRON HOMEOSTASIS"</li> | <li>Physiol Rev 93: 1721–1741, 2013 doi:10.1152/physrev.00008.2013 - Tomas Ganz "SYSTEMIC IRON HOMEOSTASIS"</li> | ||
<li>Calculated from : Computational Modeling and Simulation of the Human Duodenum - B. Hari, S. Bakalis, P. Fryer - 2012</li> | <li>Calculated from : Computational Modeling and Simulation of the Human Duodenum - B. Hari, S. Bakalis, P. Fryer - 2012</li> | ||
| - | + | <li>Wikipedia</li> | |
<li>Calculated from : Bacterial iron homeostasis - Simon C. Andrews, Andrea K. Robinson, Francisco Rodriguez-Quinones</li> | <li>Calculated from : Bacterial iron homeostasis - Simon C. Andrews, Andrea K. Robinson, Francisco Rodriguez-Quinones</li> | ||
| - | |||
</ol> | </ol> | ||
</div> | </div> | ||
Latest revision as of 03:36, 29 October 2013
Final flush treatment model
Introduction
This model comes right after the Disease model. We now want to model the flush treatment by simulating a flush of iron-chelating bacteria.
Observations
Once our genetically modified bacteria are released in the duodenum lumen, they produce siderophores to chelate the solved iron, thus making it unavailable for intestinal absorption. Then, they eventually flush out of the duodenum. The main hypothesis in this model is that the bacteria do not colonize the duodenum : they only flow through. They do not even have time to grow, for the time required to flush through is close to 40 seconds.
Because some of the parameters remain unknown, it is a theoretical simulation which will not give any numerical results, only qualitative results.
Goal
This model was made to check if our first strategy was viable. It aims to answer the following question:
"Is it possible to chelate a significant amount of iron with a flush strategy?"
Assumptions
The same assumptions as in the previous model apply:- Our bacteria don't settle in the duodenum
- No regulation in the patient's iron absorption
- Constant iron flow in the duodenum lumen
- Homogeneous fluid
- The bacterial quantity is constant
- The bacterial natural absorption is insignificant compared to the chelation
- The patient ingests 20mg of iron per day (Guideline Daily Amounts)
Materials and methods
 A : Total quantity of iron absorbed by the duodenum (mol)
A : Total quantity of iron absorbed by the duodenum (mol)
S : Quantity of solved iron (mol)
P : Total quantity of enterobactin produced by our population of bacteria (mol)
Q : Total quantity of chelated iron (mol)
N : Number of bacteria

| Sp | mol.s-1 | Iron pulse |
| v | m.s-1 | Chyme's flow average speed |
| L | m | Duodenum length |
| α | s-1 | Duodenum absorption rate |
| K | mol/s | Activator Magnitude |
| p | mol.s-1 | Value at zero of the activator |
| h | - | Activator efficiency |
| d | mol | Activator threshold |
| δ | mol-1 | Chelation rate |
The graph on the right explains the reasoning: for instance, the arrow with a + between N and P means that the variation of P has a positive linear term in N. Where
 is our Logistic function (which we will here abusively call activator).
is our Logistic function (which we will here abusively call activator).Results
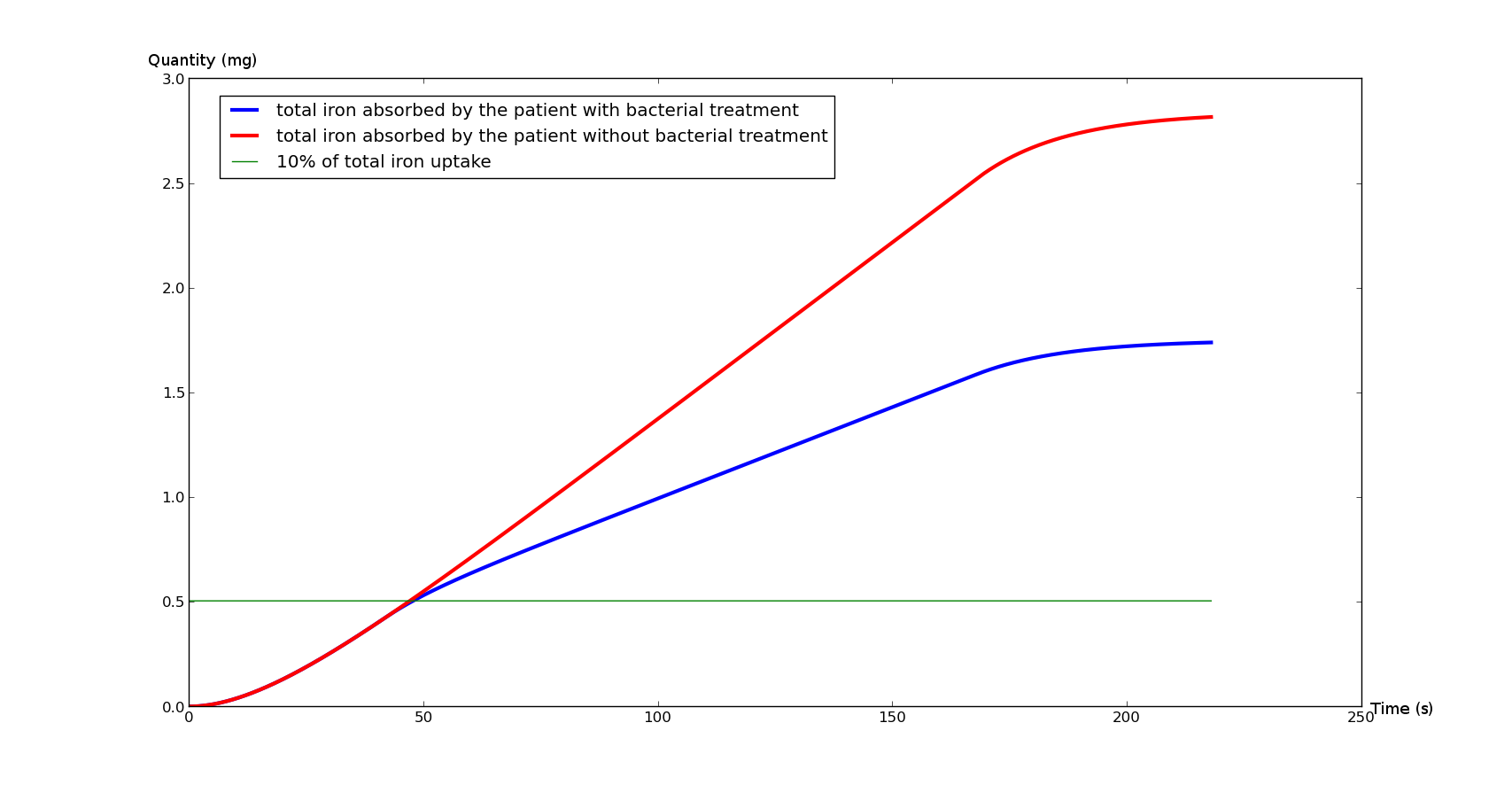
The Figure 1 represents the total iron absorbed by the duodenum during an average meal (with and without bacterial treatment), whereas the Figure 2 represents the instant ambient iron in the duodenum lumen(with and without bacterial treatment).
The Figure 2 points out the influence of our bacteria on the middle. The blue curve decreases significantly under the bacterial flow. That underlines the fact that the treatment doesn't directly affect the absorption. After 150 seconds, the chyme is considered to progressively leave the duodenum (entering the jejunum), thus reducing the iron absorption in both cases, which finally leads to a steady state.
Parameters:
The simulations was made with following parameters:| Name | Value | Unit | Description | Reference |
|---|---|---|---|---|
| Sp | 4.5*10-9 | mol.s-1 | Iron pulse | [1][2] |
| v | 0.007 | m.s-1 | Chyme's flow average speed | [2] |
| L | 0.3 | m | Duodenum length | [3] |
| α | 0.03 | s-1 | Duodenum absorption rate | Disease model |
| K | 100 | mol/s | Activator Magnitude | set |
| p | 0.005 | mol.s-1 | Value at zero of the activator | set |
| h | 10-5 | - | Activator efficiency | set |
| d | 10-9 | mol | Activator threshold | [4] |
| δ | 2.65*10-8 | mol-1 | Chelation rate | [4] |
Conclusion
The combination of the two curves clearly shows that bacteria would be able to neutralize a significant quantity of iron before it is absorbed by the duodenum.
It would thus be possible to approximately divide the intestinal iron intake by 2 if the patient takes one pill during each meal. This means that the patient would endure a lighter treatment : less bloodletting for people suffering from hemochromatosis, and less iron chelator's side effects for the thalassemia.
Models and scripts
This model was made using the Python language. You can download the python script here.
References:
- Physiol Rev 93: 1721–1741, 2013 doi:10.1152/physrev.00008.2013 - Tomas Ganz "SYSTEMIC IRON HOMEOSTASIS"
- Calculated from : Computational Modeling and Simulation of the Human Duodenum - B. Hari, S. Bakalis, P. Fryer - 2012
- Wikipedia
- Calculated from : Bacterial iron homeostasis - Simon C. Andrews, Andrea K. Robinson, Francisco Rodriguez-Quinones
 "
"