Team:TU-Eindhoven/PBPK
From 2013.igem.org
(→Parameter Estimation) |
JacquesErnes (Talk | contribs) (→Simulation Result) |
||
| (16 intermediate revisions not shown) | |||
| Line 4: | Line 4: | ||
=Ganciclovir Distribution= | =Ganciclovir Distribution= | ||
{{:Team:TU-Eindhoven/Template:Lead}} | {{:Team:TU-Eindhoven/Template:Lead}} | ||
| - | Ganciclovir is the prodrug to kill the bacteria. See the description page for [[Team:TU-Eindhoven/KillingMechanism | the principle of killing]]. The bacteria needs to be killed at a mild rate. So it is important to predict the concentration of | + | Ganciclovir is the prodrug to kill the bacteria. See the description page for [[Team:TU-Eindhoven/KillingMechanism | the principle of killing]]. The bacteria needs to be killed at a mild rate. So it is important to predict the concentration of Ganciclovir in the body, especially in the tumor zone as the bacteria gather in this site. In this part we used {{:Team:TU-Eindhoven/Template:Tooltip | text=PBPK | tooltip=Physiologically based pharmacokinetics model }} to describe the distribution of the drug in different tissues of body. |
{{:Team:TU-Eindhoven/Template:LeadEnd}} | {{:Team:TU-Eindhoven/Template:LeadEnd}} | ||
| - | ==Physiologically Based | + | ==Physiologically Based Pharmacokinetics Model== |
| - | The | + | The pharmacokinetics model is a useful tool to predict drug concentrations in human tissues. It models 3 processes in drug consumption: |
<big>'''1'''</big> '''Absorption''' describes how the drug enters to blood stream via different method of administration. | <big>'''1'''</big> '''Absorption''' describes how the drug enters to blood stream via different method of administration. | ||
| Line 18: | Line 18: | ||
And all the processes are modeled with differential equations. | And all the processes are modeled with differential equations. | ||
| - | The essence of | + | The essence of pharmacokinetics model is |
* '''Compartmental method'''. Different tissues in human are modeled as compartments, like lung, kidney and fat. Within the compartment, it is assumed that drug distribution is uniform. The blood flows from one compartment to another and brings the drug throughout the body. | * '''Compartmental method'''. Different tissues in human are modeled as compartments, like lung, kidney and fat. Within the compartment, it is assumed that drug distribution is uniform. The blood flows from one compartment to another and brings the drug throughout the body. | ||
| - | * '''Diffusion limitation'''. Diffusion limitation is illustrated by the speed of blood flow and the affinity of the compartment to the drug. Some organs have a higher rate of blood flow, like | + | * '''Diffusion limitation'''. Diffusion limitation is illustrated by the speed of blood flow and the affinity of the compartment to the drug. Some organs have a higher rate of blood flow, like the lungs and kidneys. In these compartments, the concentration will change faster. Different compartments also have a different affinity to the drug. Affinity depends on the chemical composition of the drug and the human tissue. But generally, the kidneys always have the highest affinity as it is the main elimination compartment. |
==Model Construction== | ==Model Construction== | ||
| - | The construction of | + | The construction of a pharmacokinetics model involves several steps. Although the principle of a pharmacokinetics model looks quite simple, every design of the model should be backed up with good reasons. |
===Tissue Grouping=== | ===Tissue Grouping=== | ||
| Line 32: | Line 32: | ||
{{:Team:TU-Eindhoven/Template:FloatEnd | caption=Tissue Grouping | id=PBPKtissue }} | {{:Team:TU-Eindhoven/Template:FloatEnd | caption=Tissue Grouping | id=PBPKtissue }} | ||
| - | In PBPK, the number of compartments depends on the data availability, aim of the study and the calculation method. There are many variations in PBPK models. But they all share the basic traits:<br> | + | In PBPK, the number of compartments depends on the data availability, aim of the study and the calculation method. There are many variations in PBPK models. But they all share the same basic traits:<br> |
* One compartment for venous blood,<br> | * One compartment for venous blood,<br> | ||
* One compartment for arterial blood,<br> | * One compartment for arterial blood,<br> | ||
| Line 39: | Line 39: | ||
Generally, as the number of compartments increases, the accuracy of prediction is improving. But the estimation error also increases as the data availability is limited. What is usually done is to lump together tissues with similar pharmacokinetical and toxicological properties. However these data are still not there for Ganciclovir. | Generally, as the number of compartments increases, the accuracy of prediction is improving. But the estimation error also increases as the data availability is limited. What is usually done is to lump together tissues with similar pharmacokinetical and toxicological properties. However these data are still not there for Ganciclovir. | ||
| - | The rule of thumb in designing | + | The rule of thumb in designing compartments is to ensure that the blood flow in each direction sums up to the cardiac output. So the two compartments, rapidly perfused tissue and slowly perfused tissue, are always used to compensate the blood flow. |
| - | Our model is mainly based on the study of J.Ren et al.{{:Team:TU-Eindhoven/Template:Ref | id=GCVtissuedistribution | author=J.Ren et al | title=Tissue distribution of borneol-modified | + | Our model is mainly based on the study of J.Ren et al.{{:Team:TU-Eindhoven/Template:Ref | id=GCVtissuedistribution | author=J.Ren et al | title=Tissue distribution of borneol-modified Ganciclovir-loaded solid lipd nanoparticles in mice after intravenous administration | journal=European Jounal of Pharmaceutics and Biopharmaceutics | edition=83 | pages=141-148 | year=2013 }} They tested the tissue concentrations of several organs in mice. Based on their results, firstly the compartments of brain, kidney, liver, spleen and lung are decided. As the aim is to predict the drug concentration in tumor zone, the compartment of tumor is also included in the model. To ensure that the blood flow sums up to total cardiac output, the rapidly perfused tissue and slowly perfused tissue are added. |
In the end the structure looks like {{:Team:TU-Eindhoven/Template:Figure | id=PBPKtissue }}. | In the end the structure looks like {{:Team:TU-Eindhoven/Template:Figure | id=PBPKtissue }}. | ||
===Route of Absorption and Elimination=== | ===Route of Absorption and Elimination=== | ||
| - | The Ganciclovir is administrated intravenously. So the initial condition in the model will be setting a concentration value to the venous blood. The drug is eliminated mainly through the | + | The Ganciclovir is administrated intravenously. So the initial condition in the model will be setting a concentration value to the venous blood. The drug is eliminated mainly through the kidneys{{:Team:TU-Eindhoven/Template:RefAgain | id=PBPKelimin}}, so in the model the kidney is the only elimination compartment. |
===Formulation=== | ===Formulation=== | ||
| Line 53: | Line 53: | ||
{{:Team:TU-Eindhoven/Template:FloatEnd | caption=Schematic of PBPK Model | id=PBPKscheme }} | {{:Team:TU-Eindhoven/Template:FloatEnd | caption=Schematic of PBPK Model | id=PBPKscheme }} | ||
| - | The PBPK model uses ordinary differential equations and the state vectors are the drug concentrations of the compartments. The different affinities of tissues to the drug | + | The PBPK model uses ordinary differential equations and the state vectors are the drug concentrations of the compartments. The different affinities of tissues to the drug are modeled as partition coefficients when the blood flows out of tissue. |
| - | For compartments | + | For compartments kidney, brain, Rapidly-Perfused-Tissue, Slowly-Perfused-Tissue and tumor, the equations can be generalized as: (subscript 'co' for compartment)<br> |
<html>$$ | <html>$$ | ||
\eqalignno{ | \eqalignno{ | ||
| Line 82: | Line 82: | ||
===Parameter Estimation=== | ===Parameter Estimation=== | ||
| - | There are two types of data in PBPK | + | There are two types of data in PBPK models, the drug-nonspecific data and the drug-specific data. For each compartment, we need to estimate the blood flow, tissue volume and partition coefficient. We also need to know the elimination compartment and it's elimination rate. |
<big><big>'''1'''</big></big> '''drug-nonspecific parameters'''<br> | <big><big>'''1'''</big></big> '''drug-nonspecific parameters'''<br> | ||
| - | The tissue volumes and the blood flows are taken from the mean values of human | + | The tissue volumes and the blood flows are taken from the mean values of human adults. The blood flows of brain, kidney, liver, spleen and lung are estimated from the study of Feras Khalil and Stephanie Laer.{{:Team:TU-Eindhoven/Template:Ref | id=PBPKvolume | author=Feras Khalil and Stephanie Laer | title=Physiologically Based Pharmacokinetics Modeling: Methodology, Applications, and Limitations with a Focus on Its Role in Pediatric Drug Development | journal=Journal of Biomedicine and Biotechnology | edition= | pages= | year=2011 }} The volumes of these organs are from L. Birnbaum et al. {{:Team:TU-Eindhoven/Template:Ref | id=PBPKparam | author=L.Birnbaum et al | title= |journal=Physiological Parameter Values for PBPK Models| edition= | pages= | year=1994 }}.<br> |
| - | The tissue volumes of the rapidly perfuse tissue and the slowly perfuse tissue are estimated from the study by J.H.Sung et al by keeping the same ratio to liver. {{:Team:TU-Eindhoven/Template:Ref | id=PBPKtumor | author=Jong Hwan Sung et al | title=A Combined Pharmacokinetic-Pharmacodynamic(PK-PD) Model for Tumor Growth in the Rat with UFT Administration |journal=Journal of Pharmaceutical Science| edition=98 | pages= | year=2009 }}. The blood flows of these two compartments are taken from the same research. The values are scaled so that the blood flow sums up to cardiac output. Then the tumor is separated from slowly | + | The tissue volumes of the rapidly perfuse tissue and the slowly perfuse tissue are estimated from the study by J.H.Sung et al by keeping the same ratio to liver. {{:Team:TU-Eindhoven/Template:Ref | id=PBPKtumor | author=Jong Hwan Sung et al | title=A Combined Pharmacokinetic-Pharmacodynamic(PK-PD) Model for Tumor Growth in the Rat with UFT Administration |journal=Journal of Pharmaceutical Science| edition=98 | pages= | year=2009 }}. The blood flows of these two compartments are taken from the same research. The values are scaled so that the blood flow sums up to cardiac output. Then the tumor is separated from slowly perfused tissue with the volume assumed to be 1% of the body volume.<br> |
The result of tissue volume and blood flow: | The result of tissue volume and blood flow: | ||
{|class="table table-striped" | {|class="table table-striped" | ||
| Line 113: | Line 113: | ||
| 1 | | 1 | ||
|- | |- | ||
| - | | | + | | RapidPerfused |
| 0.025 | | 0.025 | ||
| 0.2078 | | 0.2078 | ||
|- | |- | ||
| - | | | + | | SlowPerfused |
| 0.4875 | | 0.4875 | ||
| 0.170 | | 0.170 | ||
| Line 131: | Line 131: | ||
{{:Team:TU-Eindhoven/Template:FloatEnd | caption=Data optimization in PBPK | id=PBPKoptim }} | {{:Team:TU-Eindhoven/Template:FloatEnd | caption=Data optimization in PBPK | id=PBPKoptim }} | ||
The partition coefficients are drug specific parameters. It equals the ratio of concentrations between two connected compartments during equilibrium. Ideally, it should be tested in the lab by administrating the drug continuously till the drug concentrations reach steady state in the tissues. But these data are very rare. Based on the available data{{:Team:TU-Eindhoven/Template:RefAgain | id=PBPKparam}}, the '''area method'''{{:Team:TU-Eindhoven/Template:Ref | id=PBPKareaMethod | author=James M.Gallo et al | title=Area Method for the Estimation of Partition Coefficients for Physiological Pharmacokinetic Models |journal=Journal of Pharmacokinetics and Biopharmaceutics | edition=15 | pages= | year=1987 }} is used in combination with '''parameter optimization''' to estimate the partition coefficient.<br> | The partition coefficients are drug specific parameters. It equals the ratio of concentrations between two connected compartments during equilibrium. Ideally, it should be tested in the lab by administrating the drug continuously till the drug concentrations reach steady state in the tissues. But these data are very rare. Based on the available data{{:Team:TU-Eindhoven/Template:RefAgain | id=PBPKparam}}, the '''area method'''{{:Team:TU-Eindhoven/Template:Ref | id=PBPKareaMethod | author=James M.Gallo et al | title=Area Method for the Estimation of Partition Coefficients for Physiological Pharmacokinetic Models |journal=Journal of Pharmacokinetics and Biopharmaceutics | edition=15 | pages= | year=1987 }} is used in combination with '''parameter optimization''' to estimate the partition coefficient.<br> | ||
| - | Firstly, the ratios of Area Under the Curve(AUC) are calculated. | + | Firstly, the ratios of the Area Under the Curve(AUC) are calculated. This data is then used as an initial guess in the parameter optimization. Note that we can only get data for brain, kidney, liver, spleen and lung, the partition coefficient of rapidly perfused tissue is kept the same as the biggest value and those of slowly perfused tissue and tumor are kept the same as the smallest value. Then the simulation is run at once to get the new values of AUCs. The differences are the objective vectors to minimize. |
| - | The elimination rate is also drug specific. Steven McGloughlin et al.{{:Team:TU-Eindhoven/Template:Ref | id=PBPKelimin | author=Steven McGloughlin et al | title=Ganciclovir pharmacokinetics and suggested dosing in continuous | + | The elimination rate is also drug specific. Steven McGloughlin et al.{{:Team:TU-Eindhoven/Template:Ref | id=PBPKelimin | author=Steven McGloughlin et al | title=Ganciclovir pharmacokinetics and suggested dosing in continuous venous haemodiafiltration |journal=International Journal of Antimicrobial Agents| edition=37 | pages=82-92 | year=2011 }} mentioned that kidney is the main elimination compartment for Ganciclovir and the apparent elimination rate is 0.049 h<sup>-1</sup>. The parameter optimization is also used to estimate the real elimination rate. The initial guess is the apparent elimination rate times the ratio of cardiac output to the blood flow of kidney, i.e., 0.196 h<sup>-1</sup>. |
The scheme of data optimization is shown in {{:Team:TU-Eindhoven/Template:Figure | id=PBPKoptim }}. | The scheme of data optimization is shown in {{:Team:TU-Eindhoven/Template:Figure | id=PBPKoptim }}. | ||
| Line 164: | Line 164: | ||
| 1.2529 | | 1.2529 | ||
|- | |- | ||
| - | | | + | | RapidPerfused<sup>1</sup> |
| 2.1054 | | 2.1054 | ||
| 2.0100 | | 2.0100 | ||
|- | |- | ||
| - | | | + | | SlowPerfused<sup>2</sup> |
| 0.1150 | | 0.1150 | ||
| 0.1150 | | 0.1150 | ||
| Line 184: | Line 184: | ||
| 1.2748 | | 1.2748 | ||
|} | |} | ||
| - | ''1. The value of rapidly | + | ''1. The value of rapidly perfused tissue is kept the same with the highest partition coefficient, i.e., in the kidney;''<br> |
| - | ''2. The values of tumor and slowly | + | ''2. The values of tumor and slowly perfused tissue are kept the same with the lowest partition coefficient. |
==Simulation Result== | ==Simulation Result== | ||
| - | The result of simulation with the estimated data is: | + | The result of a simulation with the estimated data is: |
{{:Team:TU-Eindhoven/Template:Image | filename=PBPKresult.png}} | {{:Team:TU-Eindhoven/Template:Image | filename=PBPKresult.png}} | ||
| Line 194: | Line 194: | ||
==References== | ==References== | ||
{{:Team:TU-Eindhoven/Template:RefList}} | {{:Team:TU-Eindhoven/Template:RefList}} | ||
| + | |||
| + | '''The source code of all models can be found [[Team:TU-Eindhoven/Code:Models | here]].''' | ||
{{:Team:TU-Eindhoven/Template:BaseFooter}} | {{:Team:TU-Eindhoven/Template:BaseFooter}} | ||
Latest revision as of 15:03, 26 October 2013



Contents |
Ganciclovir Distribution
Ganciclovir is the prodrug to kill the bacteria. See the description page for the principle of killing. The bacteria needs to be killed at a mild rate. So it is important to predict the concentration of Ganciclovir in the body, especially in the tumor zone as the bacteria gather in this site. In this part we used PBPK to describe the distribution of the drug in different tissues of body.
Physiologically Based Pharmacokinetics Model
The pharmacokinetics model is a useful tool to predict drug concentrations in human tissues. It models 3 processes in drug consumption:
1 Absorption describes how the drug enters to blood stream via different method of administration.
2 Distribution is how the drug distributes into different human tissues.
3 Elimination is the process that the drug is eliminated from blood stream.
And all the processes are modeled with differential equations.
The essence of pharmacokinetics model is
- Compartmental method. Different tissues in human are modeled as compartments, like lung, kidney and fat. Within the compartment, it is assumed that drug distribution is uniform. The blood flows from one compartment to another and brings the drug throughout the body.
- Diffusion limitation. Diffusion limitation is illustrated by the speed of blood flow and the affinity of the compartment to the drug. Some organs have a higher rate of blood flow, like the lungs and kidneys. In these compartments, the concentration will change faster. Different compartments also have a different affinity to the drug. Affinity depends on the chemical composition of the drug and the human tissue. But generally, the kidneys always have the highest affinity as it is the main elimination compartment.
Model Construction
The construction of a pharmacokinetics model involves several steps. Although the principle of a pharmacokinetics model looks quite simple, every design of the model should be backed up with good reasons.
Tissue Grouping
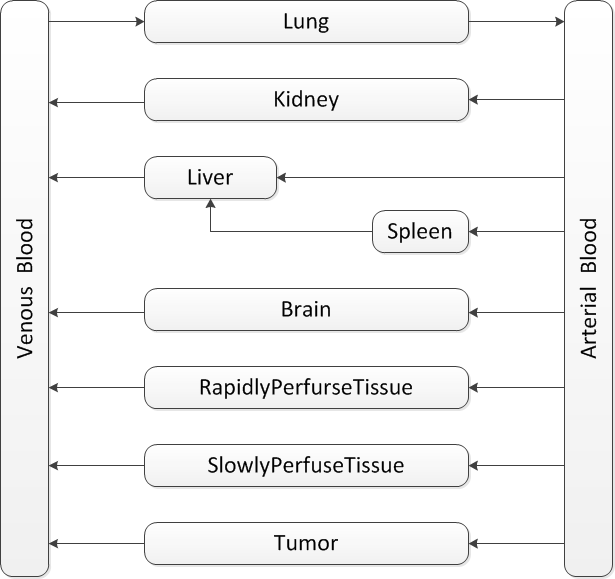
In PBPK, the number of compartments depends on the data availability, aim of the study and the calculation method. There are many variations in PBPK models. But they all share the same basic traits:
- One compartment for venous blood,
- One compartment for arterial blood,
- At least one elimination compartment and,
- At least one absorption compartment.
Generally, as the number of compartments increases, the accuracy of prediction is improving. But the estimation error also increases as the data availability is limited. What is usually done is to lump together tissues with similar pharmacokinetical and toxicological properties. However these data are still not there for Ganciclovir.
The rule of thumb in designing compartments is to ensure that the blood flow in each direction sums up to the cardiac output. So the two compartments, rapidly perfused tissue and slowly perfused tissue, are always used to compensate the blood flow.
Our model is mainly based on the study of J.Ren et al.GCVtissuedistributionJ.Ren et al, Tissue distribution of borneol-modified Ganciclovir-loaded solid lipd nanoparticles in mice after intravenous administration. European Jounal of Pharmaceutics and Biopharmaceutics 83, 141-148 (2013) They tested the tissue concentrations of several organs in mice. Based on their results, firstly the compartments of brain, kidney, liver, spleen and lung are decided. As the aim is to predict the drug concentration in tumor zone, the compartment of tumor is also included in the model. To ensure that the blood flow sums up to total cardiac output, the rapidly perfused tissue and slowly perfused tissue are added.
In the end the structure looks like .
Route of Absorption and Elimination
The Ganciclovir is administrated intravenously. So the initial condition in the model will be setting a concentration value to the venous blood. The drug is eliminated mainly through the kidneysPBPKelimin, so in the model the kidney is the only elimination compartment.
Formulation

The PBPK model uses ordinary differential equations and the state vectors are the drug concentrations of the compartments. The different affinities of tissues to the drug are modeled as partition coefficients when the blood flows out of tissue.
For compartments kidney, brain, Rapidly-Perfused-Tissue, Slowly-Perfused-Tissue and tumor, the equations can be generalized as: (subscript 'co' for compartment)
$$
\eqalignno{
\dot{C_{co}} & = \color{red}{Q_{co} C_{Art}} - \color{#08F}{\frac{Q_{co}}{K_{co}} C_{co}}
}$$
For the lung, the direction of blood flow is inversed:
$$
\eqalignno{
\dot{C_{Lu}} & = \color{#08F}{Q_{Lu} C_{Ven}} - \color{red}{\frac{Q_{Lu}}{K_{Lu}} C_{Lu}}\\
}$$
For the compartment of liver and spleen, the blood outflow from the spleen goes directly into the liver:
$$
\eqalignno{
\dot{C_{Li}} & = \color{red}{(Q_{Li}-Q_{Sp}) C_{Art}} + \frac{Q_{Sp}}{K_{Sp}} C_{Sp} - \color{#08F}{\frac{Q_{Lu}}{K_{Lu}} C_{Lu}}\\
\dot{C_{Sp}} & = \color{red}{Q_{Sp} C_{Art}} - \color{#08F}{\frac{Q_{Sp}}{K_{Sp}} C_{Sp}}\\
}$$
Finally for the arterial blood and venous blood:
$$
\eqalignno{
\color{#08F}{\dot{C_{Ven}}} & = \color{#08F}{\sum_{co}{\frac{Q_{co}}{K_{co}} C_{co}}} - \color{#08F}{Q_{Lu} C_{Lu}}\\
\color{red}{\dot{C_{Art}}} & = \color{red}{Q_{Lu} C_{Lu}} - \color{red}{\sum_{co}{\frac{Q_{co}}{K_{co}} C_{co}}}, for~co = Ki, Li, Br, Ra, Sl~and~Tu\\
}$$
Parameter Estimation
There are two types of data in PBPK models, the drug-nonspecific data and the drug-specific data. For each compartment, we need to estimate the blood flow, tissue volume and partition coefficient. We also need to know the elimination compartment and it's elimination rate.
1 drug-nonspecific parameters
The tissue volumes and the blood flows are taken from the mean values of human adults. The blood flows of brain, kidney, liver, spleen and lung are estimated from the study of Feras Khalil and Stephanie Laer.PBPKvolumeFeras Khalil and Stephanie Laer, Physiologically Based Pharmacokinetics Modeling: Methodology, Applications, and Limitations with a Focus on Its Role in Pediatric Drug Development. Journal of Biomedicine and Biotechnology , (2011) The volumes of these organs are from L. Birnbaum et al. PBPKparamL.Birnbaum et al, . Physiological Parameter Values for PBPK Models , (1994).
The tissue volumes of the rapidly perfuse tissue and the slowly perfuse tissue are estimated from the study by J.H.Sung et al by keeping the same ratio to liver. PBPKtumorJong Hwan Sung et al, A Combined Pharmacokinetic-Pharmacodynamic(PK-PD) Model for Tumor Growth in the Rat with UFT Administration. Journal of Pharmaceutical Science 98, (2009). The blood flows of these two compartments are taken from the same research. The values are scaled so that the blood flow sums up to cardiac output. Then the tumor is separated from slowly perfused tissue with the volume assumed to be 1% of the body volume.
The result of tissue volume and blood flow:
| Compartment | Fraction of body volume | Fraction of cardiac output |
|---|---|---|
| Brain | 0.017 | 0.1162 |
| Kidney | 0.0044 | 0.25 |
| Liver | 0.026 | 0.227 |
| Spleen | 0.0023 | 0.028 |
| Lung | 0.007 | 1 |
| RapidPerfused | 0.025 | 0.2078 |
| SlowPerfused | 0.4875 | 0.170 |
| Tumor | 0.001 | 0.001 |
2 drug-specific parameters

Firstly, the ratios of the Area Under the Curve(AUC) are calculated. This data is then used as an initial guess in the parameter optimization. Note that we can only get data for brain, kidney, liver, spleen and lung, the partition coefficient of rapidly perfused tissue is kept the same as the biggest value and those of slowly perfused tissue and tumor are kept the same as the smallest value. Then the simulation is run at once to get the new values of AUCs. The differences are the objective vectors to minimize.
The elimination rate is also drug specific. Steven McGloughlin et al.PBPKeliminSteven McGloughlin et al, Ganciclovir pharmacokinetics and suggested dosing in continuous venous haemodiafiltration. International Journal of Antimicrobial Agents 37, 82-92 (2011) mentioned that kidney is the main elimination compartment for Ganciclovir and the apparent elimination rate is 0.049 h-1. The parameter optimization is also used to estimate the real elimination rate. The initial guess is the apparent elimination rate times the ratio of cardiac output to the blood flow of kidney, i.e., 0.196 h-1.
The scheme of data optimization is shown in . The keobs in the figure stands for the observed elimination rate, i.e., the apparent elimination rate.
The result of data optimization is:
| Partition coefficient | Initial guess | Data optimization result |
|---|---|---|
| Brain | 0.1150 | 0.1150 |
| Kidney | 2.1054 | 2.0100 |
| Liver | 0.7087 | 0.7091 |
| Spleen | 1.6475 | 1.1682 |
| Lung | 1.2180 | 1.2529 |
| RapidPerfused1 | 2.1054 | 2.0100 |
| SlowPerfused2 | 0.1150 | 0.1150 |
| Tumor2 | 0.001 | 0.001 |
| Elimination rate | ||
| Total elimination rate | 0.196 | 1.2748 |
1. The value of rapidly perfused tissue is kept the same with the highest partition coefficient, i.e., in the kidney;
2. The values of tumor and slowly perfused tissue are kept the same with the lowest partition coefficient.
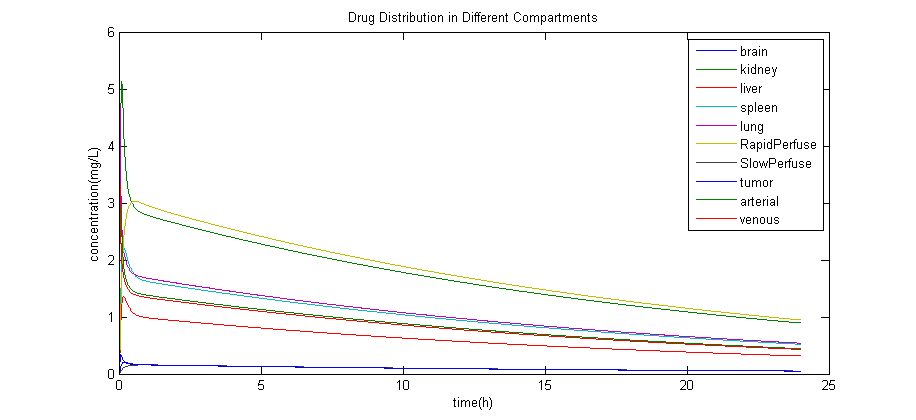
Simulation Result
The result of a simulation with the estimated data is:
References
The source code of all models can be found here.
 "
"



