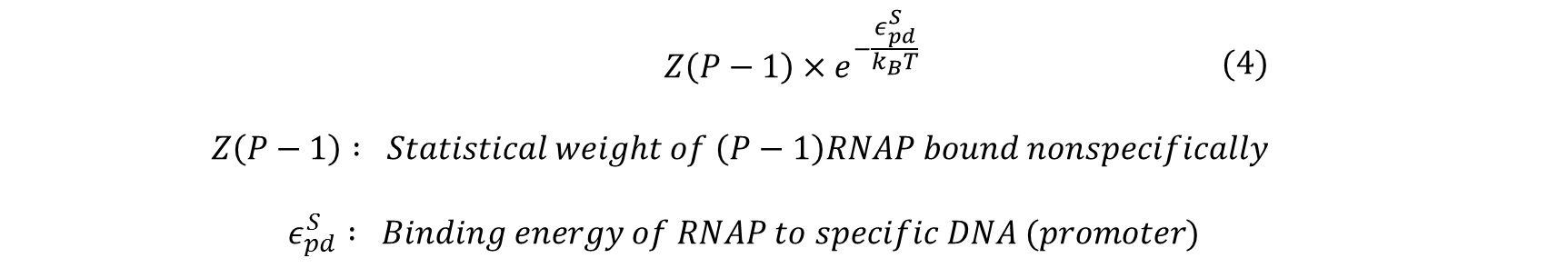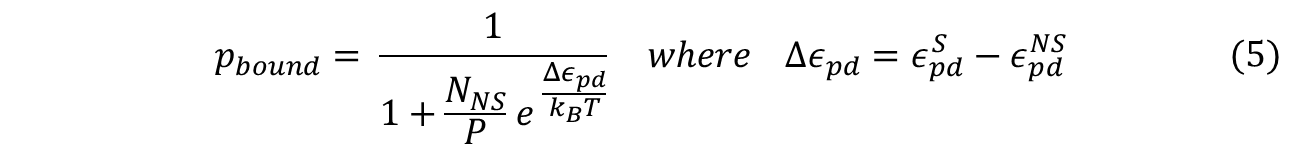Mathematical Modeling of Bistable Toggle Switch

Thermodynamic Model of Cooperative Repression

Introduction

A thermodynamic approach was used to model the cooperative repression by transcription factors (iTAL and CRISPR) binding to multiple binding sites. The model was largely based on the models shown in "Transcriptional regulation by the numbers: models" (Bintu, 2005), which base on the reasoning that gene expression level is related to the probabilities of various molecules--such as transcription factors (TFs) and RNA Polymerase (RNAP)--binding to the DNA of interest. The key concept in this model is using the "probability that RNAP occupies the promoter of interest" instead of using "concentration of protein" produced. One of the most important assumptions of this model is that promoter occupancy by RNAP is directly proportional to the level of gene expression.

Simple Case (No Transcription Factors)

First, let's start with the case without any transcription factors. In this simple case, we will ignore the RNAPs that are in the cytoplasm or engaged in transcription, and assume that our pool of free RNAPs is the "non-specifically" bound RNAPs (Non-specific here means the protein is bound to sequences other than the target promoter). According to the paper (Bintu, 2005), the sum of Boltzmann weights of all possible states of P polymerase molecules on DNA must be calculated to evaluate the probability of RNAP bound. Shown below is a table of variables used in the calculations that follow.

All the possible outcome of P RNAP molecules binding to the genome can be classified into two:

1. all RNAP bound non-specifically, or
2. (P-1) RNAP bound non-specifically and 1 RNAP bound specifically to promoter of interest.
   

Next, we count the number of ways these two outcomes can be achieved and sum their statistical weights calculated by:

Using the above formula and combinatorics, the statistical weight of having P RNAP distributed among N_ns non-specific sites can be calculated by the following:

Similarly, the statistical weight of having (P-1) RNAP bound non-specifically and one RNAP bound specifically to the promoter of interest can be calculated by:

To obtain the probability of RNAP bound to promoter of interest, we simply divide the statistical weight of specific-binding by the total statistical weight of both states. When simplified, the following equation for probability of RNAP bound to promoter is found. (Detailed derivation can be found here: Derivation)

Case with Transcription Factors

cite bintu