Team:NYMU-Taipei/Modeling/MainParts

From 2013.igem.org

(Difference between revisions)
Line 403: Line 403:
<html>
<html>
<div lang="latex" class="equation">
<div lang="latex" class="equation">
-
\frac{d[ethanol]}{dt}=K"pyruvateacetaldehyde"\timesK"acetaldehydeethanol"\times\frac{ [PDC]^{nPDC} }{ KdPDC^{nPDC}+[PDC] }\times\frac{ [ADH]^{nADH} }{ KdADH^{nADH}+[ADH] }\times[pyruvate]-Km\times\frac{ [ADH]^{nADH} }{ KdADH^{nADH}+[ADH]^{nADH} }\times[ethanol]
+
\frac{d[ethanol]}{dt}=Kpyruvateacetaldehyde\timesKacetaldehydeethanol\times\frac{ [PDC]^{nPDC} }{ KdPDC^{nPDC}+[PDC] }\times\frac{ [ADH]^{nADH} }{ KdADH^{nADH}+[ADH] }\times[pyruvate]-Km\times\frac{ [ADH]^{nADH} }{ KdADH^{nADH}+[ADH]^{nADH} }\times[ethanol]
</div>
</div>
</html>
</html>

Revision as of 21:28, 27 September 2013

National Yang Ming University


Contents

Function of the parts:

  1. circuit regulators:
  • LacIregulatedpromoter(pLac) : when LacI exists, it will bind to LacIregulatedpromoter(pLac) and represses the promoter.
  • pLux/cIhybridpromoter(plux/cI) : when luxR/AHL exists, it will open pLux/cIhybridpromoter(plux/cI), while cI will repress the promoter. What’s more, plux/cI is cI-dominant, which means when cI exists, the hybrid promoter will be repressed whether luxR/AHL exists or not.
  1. Circuit regulation:
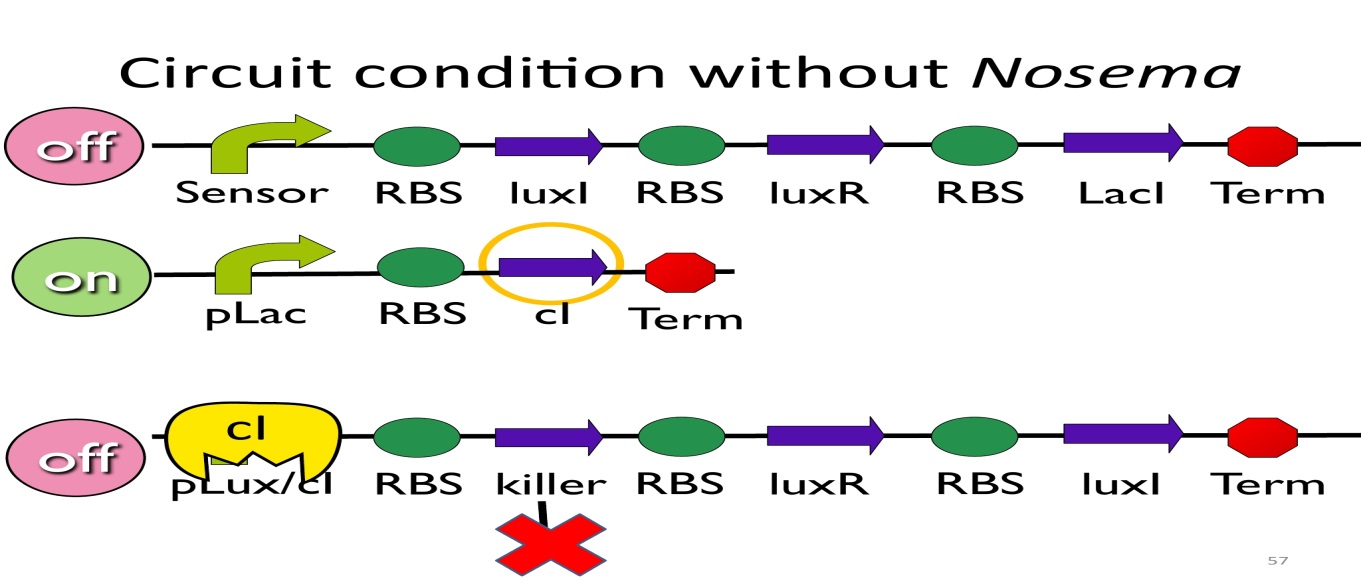
  • Circuit condition without Nosema:
NYMU-Taipei Circuit condition wo nosema.jpg

Without NosemaCeranae, the first circuit will not open, and thus, no LacI will be produced. Since there is no LacI binding to pLac, pLac will not be repressed, which means cI will be produced. After that, cIwill bind to pLux/cI-hybridpromoter, leading the third circuit to be off.

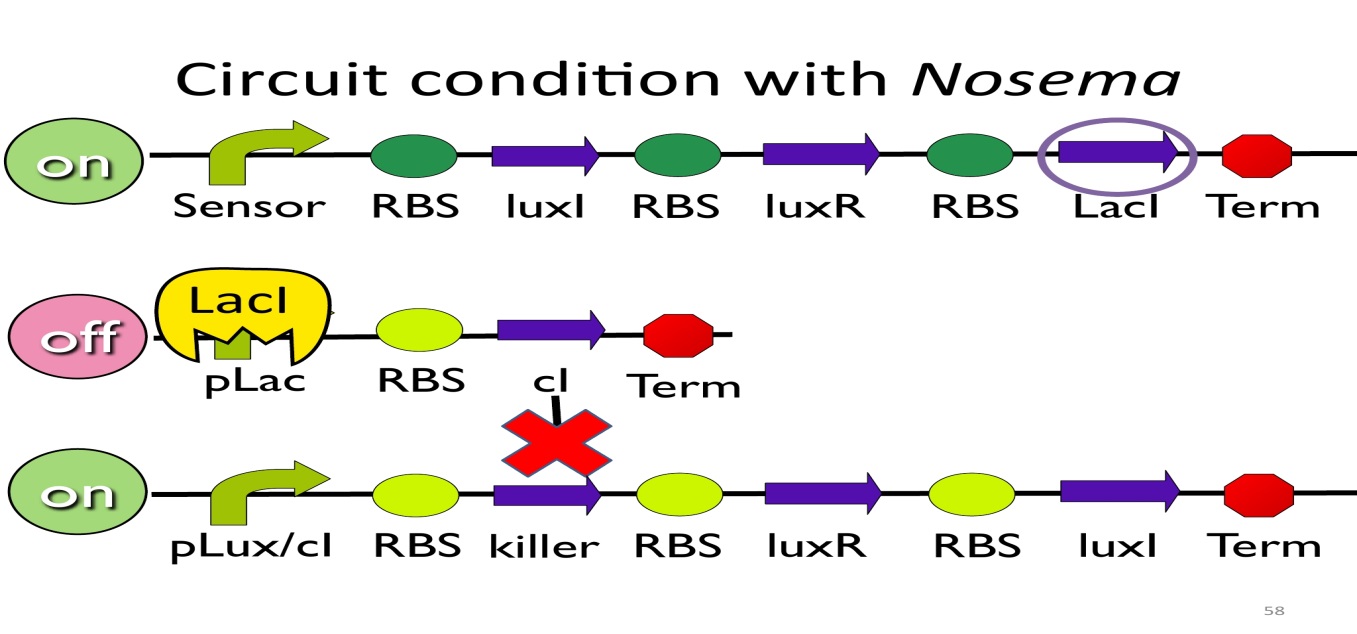
  • Circuit condition with Nosema:
NYMU-Taipei Circuit condition w nosema.jpg

When NosemaCeranae infects the bee, bee’s immune system will be activated, leading to the concentration of ROS(reactive oxygen species) to be high. In response, E. Kobee will enhance the production of oxyR, which binds to transcription binding site ahead of trxC (an oxyR-activated promoter; namely, the sensor), leading to the first circuit to be on.

Since the first circuit is on, the downstream LacI gene will be produced and bind to pLac, leading to the second circuit to be off.

After the second circuit is closed, no cI is produced, leading to the third circuit to be on (no repressor at all). And then, killer protein will be produced and kill NosemaCeranae.

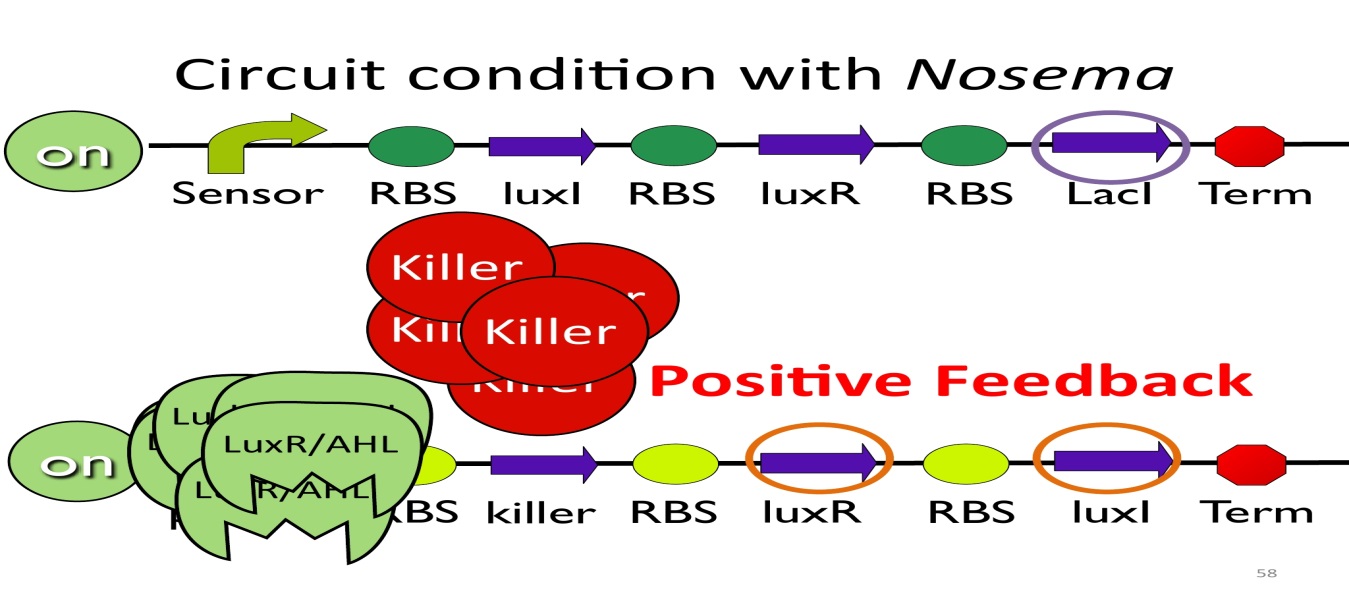
  • Positive feedback:
NYMU-Taipei Mod 3.jpg

Besides the LuxI and LuxR(which then form a complex called luxR/AHL) produced by first circuit, the third circuit will also produce luxR/AHL, which acts as a positive feedback and strongly enhances the production of killer protein.

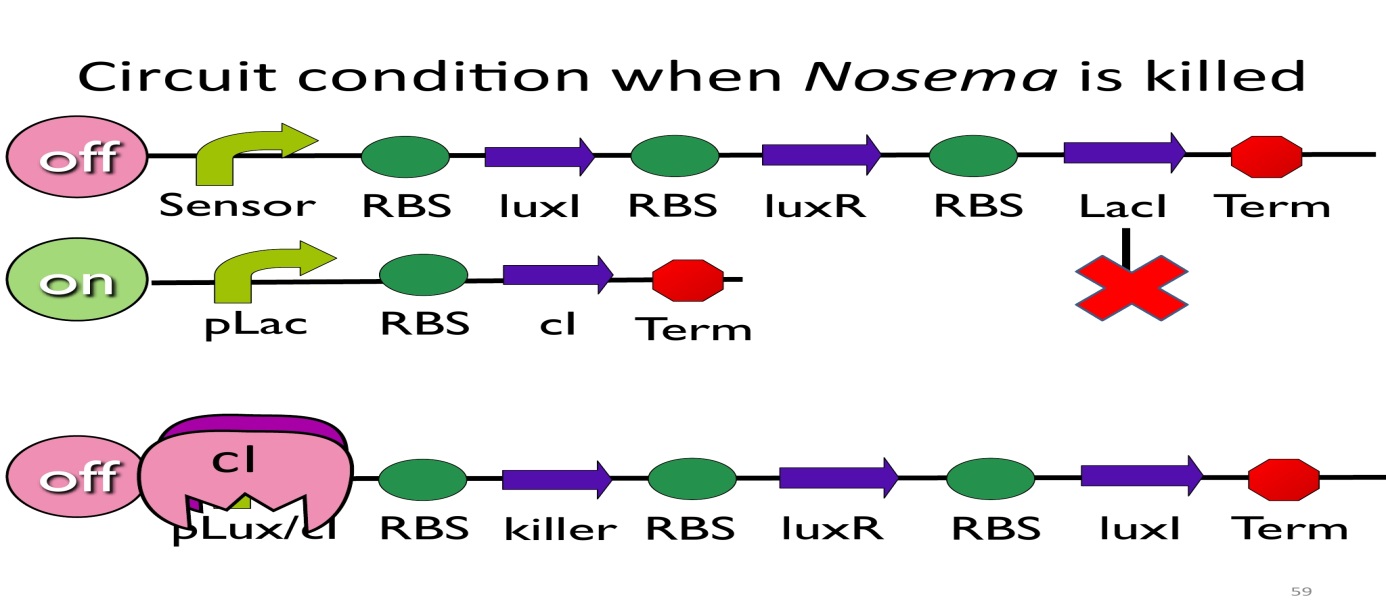
  • CircuitconditionwhenNosema is killed:
NYMU-Taipei Mod 4.jpg

After Nosema is killed, the sensor will be off and no lacI will be produced. Without LacI, the pLac will not be repressed, and the second circuit will be on, leading to the production of cI. After cI binds topLux/cIhybridpromoter, the third circuit to be off.

The overall circuit will switch to the beginning stage when there is no Nosema.

The purpose of this modeling is:

  1. To know how much time it needs from sensing to killing the Nosema after infection
  2. To know whether the pathway is effectiveor not
  3. To know the range of killer protein concentration(from the minimal concentration which Is effective to kill Nosema to the maximal concentration which will not do harm to the bees)

It is assumed that AHL is abundant and thus the formation of AHL2LuxR is determined only by the concentration of LuxR; CI’s mechanism of binding to the promoter is assumed to act as hill effect form; kill protein will sustain a period of time before it is degraded naturally without any other types of degration.

Equation1:

\frac{d[mRNACI]}{dt}=\frac{ 1-[LacI]^{nLacI} }{ KdLacI^{nLacI}+[LacI]^{nLacI} }\timesPoPSpLac\times\frac{N}{V}-kdegmRNA\times[mRNACI]

KdLacI = dissociation constant of CI

nLacI = Hill coefficient of LacI

PoPSpLac = promoter strength of pLac

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to knowmRNACI production rate and when it can reach the level to translate the desired concentration.

Equation2:

\frac{d[mRNALacI]}{dt}=\frac{ [ROSoxyR]^{nROSoxyR} }{ KdROSoxyR^{nROSoxyR}+[ROSoxyR]^{nROSoxyR} }\timesPoPStrxC\times\frac{N}{V}-kdegmRNA\times[mRNAlacI]

KdROSoxyR = dissociation constant ofROSoxyR

nROSoxyR = Hill coefficient of ROSoxyR

PoPStrxC = promoter strength of trxC

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to know how trxC promoter strength (in PoPS) influences the production of lacI.

Equation3:

\frac{d[mRNAoxyR]}{dt}=PoPSconstitutive\times\frac{N}{V}-KdegmRNA[mRNAoxyR]

PoPSconstitutive= promoter strength of constitutive promoter (J23102)

N = number of plasmid in a single cell

V = volume of a cell

kdegmRNA = degrading constant of sensor promoter mRNA

The aim of the equation is to know the production rate ofmRNAoxyR, and choose the proper constitutive promoter for boosting OxyR's concentration.

Equation4:

KdROSoxyR = dissociation constant ofROSoxyR

nROSoxyR = Hill coefficient of ROSoxyR

PoPStrxC = promoter strength of trxC

KdLuxRAHL = dissociation constant ofLuxRAHL

nLuxRAHL = Hill coefficient of LuxRAHL

KdcI = dissociation constant ofcI

ncI = Hill coefficient ofCi

PoPSLuxcI = promoter strength of LuxcI hybrid promoter

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to know how trxC promoter strength (in PoPS) influences the production of LuxI.

Equation5:

KdROSoxyR = dissociation constant ofROSoxyR

nROSoxyR = Hill coefficient of ROSoxyR

PoPStrxC = promoter strength of trxC

KdLuxRAHL = dissociation constant ofLuxRAHL

nLuxRAHL = Hill coefficient of LuxRAHL

KdcI = dissociation constant ofcI

ncI = Hill coefficient ofCi

PoPSLuxcI = promoter strength of LuxcI hybrid promoter

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to know how trxC promoter strength (in PoPS) influences the production of LuxR.

Equation6:

KdLuxRAHL = dissociation constant ofLuxRAHL

nLuxRAHL = Hill coefficient of LuxRAHL

KdcI = dissociation constant ofcI

ncI = Hill coefficient ofCi

PoPSLuxcI = promoter strength of LuxcI hybrid promoter

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to knowmRNA of kill protein production rate and when it can reach the level ofthe desired concentration.

Equation7:

KdROSoxyR = dissociation constant ofROSoxyR

nROSoxyR = Hill coefficient of ROSoxyR

PoPStrxC = promoter strength of trxC

KdT7 = dissociation constant of T7

NT7 = Hill coefficient of T7

PoPST7 = promoter strength of T7 promoter

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to knowmRNA of T7 polymerase production rate and when it can reach the level to translate enough T7 polymerase.

Equation8:

\frac{d[mRNAPDC]}{dt}=\frac{ [T7]^{nT7} }{ KdT7^{nT7}+[T7]^{nY7} }\timesPoPST7\times\frac{N}{V}-kdegmRNA\times[mRNAPDC]

KdT7 = dissociation constant of T7

NT7 = Hill coefficient of T7

PoPST7 = promoter strength of T7 promoter

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to knowmRNA of enzyme PDC production rate and when it can reach the level to translate enough PDC.

Equation9:

\frac{d[mRNAADH]}{dt}=\frac{ [T7]^{nT7} }{ KdT7^{nT7}+[T7]^{nY7} }\timesPoPST7\times\frac{N}{V}-kdegmRNA\times[mRNAADH]

KdT7 = dissociation constant of T7

NT7 = Hill coefficient of T7

PoPST7 = promoter strength of T7 promoter

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to knowmRNA of enzyme ADH production rate and when it can reach the level to translate enough ADH.

Equation10:

\frac{d[CI]}{dt}=RBS\times[mRNAcI]-KdegCI[CI]

RBS = binding site strength

KdegCI = degrading constant of CI

The aim of the equation is to know the production rate of CI and when it can reach the concentration to repress LuxCI hybrid promoter.

Equation11:

\frac{[LacI]}{dt}=RBS\times[mRNALacI]-KdegCI[LacI]

RBS = binding site strength

KdegLacI = degrading constant of LacI

The aim of the equation is to knowLacI production rate and when it can reach the concentration to repress promoter LacI

Equation12:

\frac{[LacI]}{dt}=RBS\times[mRNALacI]-KdegCI[LacI]

RBS = binding site strength

KAHL = LuxIAHL rate constant

KdegLuxI = degrading constant of LuxI

The aim of the equation is to know the production rate of LuxI concerning the LuxIAHL reaction and LuxI degrading.

Equation13:

\frac{d[LuxR]}{dt}=RBS\times[mRNALuxR]-KmAHL[AHL]-KdegLuxR[LuxR]-KonAHL\times[AHL]^2\times[LuxR]-KdegAHL[AHL]

RBS = binding site strength

KmAHL =AHLLuxI rate constant

KdegLuxR= degrading constant of LuxR

KonAHL = 2AHL + LuxR(AHL)2/LuxR complex rate constant

KdegAHL = degrading constant of AHL

The aim of the equation is to know the production rate of LuxR concerning the 2AHL + LuxR↔(AHL)2/LuxR reaction , AHL→LuxI reaction, and LuxR, AHL degrading.

Equation14:

\frac{d[AHL]}{dt}=KAHL\times[LuxI]+2\timesKoffAHL\times[AHLLuxR]-2\timesKonAHL\times[AHL]^2\times[LuxR]-KdegAHL[AHL]

KAHL = LuxIAHL rate constant

KonAHL = 2AHL + LuxR(AHL)2/LuxR complex rate constant

KoffAHL = (AHL)2/LuxR complex2AHL + LuxR rate constant

KdegAHL = degrading constant of AHL

The aim of the equation is to know the production rate of AHL concerning the LuxI→AHL reaction, 2AHL + LuxR↔(AHL)2/LuxRreaction and AHL degrading.

Equation15:

\frac{d[T7]}{dt}=RBS\times[mRNAT7]-KdegT7[T7]

RBS = binding site strength

KdegT7 = degrading constant of T7

The aim of the equation is to know the threshold concentration of oxyR to conquer the terminal and when T7 polymerase can reach the required concentration to activate T7 promoter.

Equation16:

\frac{d[PDC]}{dt}=RBS\times[mRNAPDC]-KdegPDC[PDC]

RBS = binding site strength

KdegPDC = degrading constant of PDC

The aim of the equation is to know PDC production rate and when it can reach the concentration of ethanol pathway equilibrium.

Equation17:

\frac{d[ADH]}{dt}=RBS\times[mRNAADH]-KdegADH[ADH]

RBS = binding site strength

KdegADH = degrading constant of ADH

The aim of the equation is to know ADH production rate and when it can reach the concentration of ethanol pathway equilibrium.

Equation18:

\frac{d[LuxRAHL]}{dt}=KonAHL\times[AHL]^2\times[LuxR]-KoffAHL\times[AHLLuxR]

KonAHL = 2AHL + LuxR(AHL)2/LuxR complex rate constant

KoffAHL = (AHL)2/LuxR complex2AHL + LuxR rate constant

KonAHL = 2AHL + LuxR(AHL)2/LuxR complex rate constant KoffAHL = (AHL)2/LuxR complex2AHL + LuxR rate constant

Equation19:

\frac{d[kill]}{dt}=RBS\times[mRNAkill]-Kdegkill[kill]

RBS = binding site strength

Kdegkill = degrading constant of kill

The aim of the equation is to knowkiller protein production rate and when it can reach the effective concentration to killNosema.

Equation20:

\frac{d[ethanol]}{dt}=Kpyruvateacetaldehyde\timesKacetaldehydeethanol\times\frac{ [PDC]^{nPDC} }{ KdPDC^{nPDC}+[PDC] }\times\frac{ [ADH]^{nADH} }{ KdADH^{nADH}+[ADH] }\times[pyruvate]-Km\times\frac{ [ADH]^{nADH} }{ KdADH^{nADH}+[ADH]^{nADH} }\times[ethanol]

Kpyruvateacetaldehyde= pyruvate→acetaldehyde reaction rate constant

Kacetaldehydeethanol= acetaldehyde→ethanol reaction rate constant

Km = ethanol→acetaldehyde reaction rate constant

KdPDC = dissociation constant of PDC

KdADH = dissociation constant of ADH

The aim of the equation is to know ethanol production rate and when it can reach the concentration to kill the spores of NosemaCeranae.

Explanation

Retrieved from "http://2013.igem.org/Team:NYMU-Taipei/Modeling/MainParts"