Team:Duke/Modeling/1
From 2013.igem.org
Hyunsoo kim (Talk | contribs) (→Hill Equation) |
Hyunsoo kim (Talk | contribs) (→Hill Equation) |
||
| Line 19: | Line 19: | ||
| - | In the Hill Equation shown above, | + | In the Hill Equation shown above, theta represents the percent saturation of binding sites, [L] is the ligand concentration, n is the Hill coefficient, and Kd is the dissociation constant of the ligand. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
Revision as of 00:23, 18 September 2013
Mathematical Modeling of Bistable Toggle Switch
Cooperativity
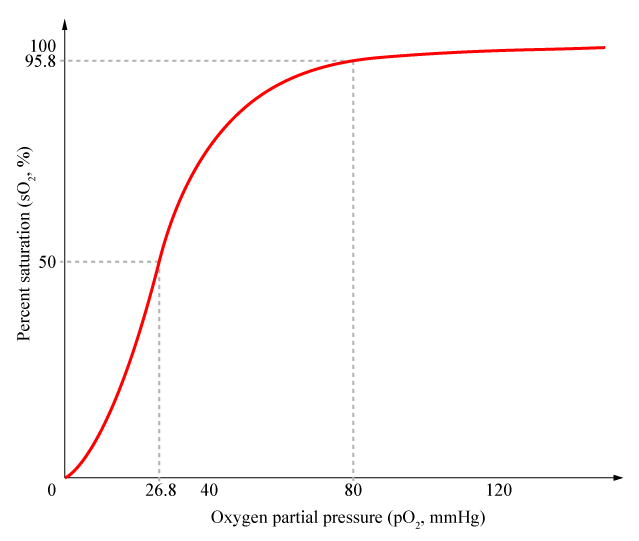
Cooperativity is a common phenomenon in biological systems involving multiple ligands binding to enzymes or receptors. The change in affinity of a binding site for a ligand upon a ligand-binding leads to either positive cooperativity in which affinity is increased and subsequent binding become more likely, or negative cooperativity in which affinity is decreased to hinder future binding. One of the most famous examples of cooperative binding is the binding of oxygen to hemoglobin, the oxygen-transporting protein in red blood cells. When an oxygen molecule bind to hemoglobin, its affinity for oxygen increases greatly, and when three oxygen molecules bind (3-oxy-hemoglobin), its affinity for the fourth one is nearly three-hundred times higher than deoxy-hemoglobin’s affinity for oxygen. This cooperative property leads to the sigmoidal shaped curve shown below.
Hill Equation
Named after English physiologist Archibald Vivian Hill who studied the sigmoidal binding curve of hemoglobin, the Hill Equation provides a way to quantify cooperativity. The equation describes the fraction of proteins or enzymes that are saturated by ligands as a function of the concentration of ligands.
In the Hill Equation shown above, theta represents the percent saturation of binding sites, [L] is the ligand concentration, n is the Hill coefficient, and Kd is the dissociation constant of the ligand.
 "
"