Team:NYMU-Taipei/Modeling/MainParts

From 2013.igem.org

(Difference between revisions)

Revision as of 13:33, 21 October 2013

National Yang Ming University

1 main part

main part

Function of the parts:

circuit regulators:

• LacI regulated promoter(pLac) : when LacI exists, it will bind to LacI regulated promoter(pLac) and represses the promoter.

• pLux/cI hybrid promoter(plux/cI) : when luxR/AHL exists, it will open pLux/cI hybrid promoter(plux/cI), while cI will repress the promoter. What’s more, plux/cI is cI-dominant, which means when cI exists, the hybrid promoter will be repressed whether luxR/AHL exists or not.

Circuit regulation:

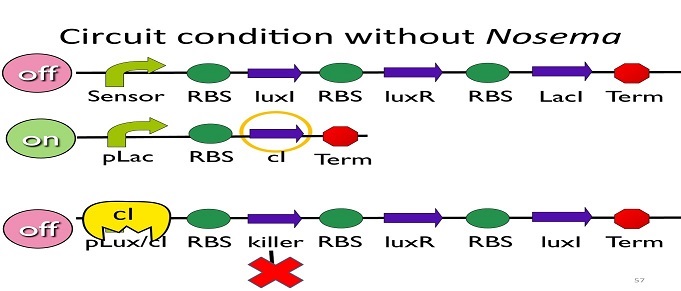
• Circuit condition without Nosema:

Without Nosema Ceranae, the first circuit will not open, and thus, no LacI will be produced. Since there is no LacI binding to pLac, pLac will not be repressed, which means cI will be produced. After that, cI will bind to pLux/cI hybrid promoter, leading the third circuit to be off.

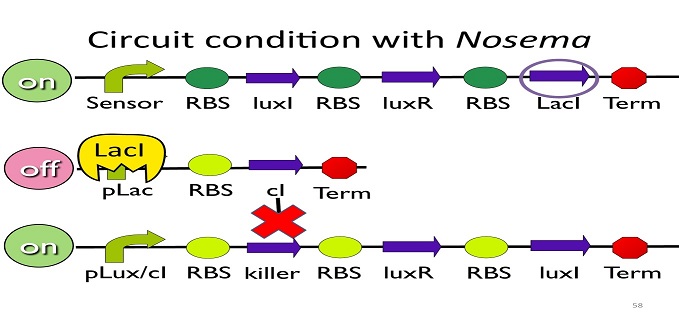
• Circuit condition with Nosema:

When Nosema Ceranae infects the bee, bee’s immune system will be activated, leading to the concentration of ROS (reactive oxygen species) to be high. In response, Bee. coli will enhance the production of oxyR, which forms a complex with ROS and binds to transcription binding site ahead of trxC (an oxyR-activated promoter; namely, the sensor), leading to the first circuit to be on.

Since the first circuit is on, the downstream LacI gene will be produced and bind to pLac, leading to the second circuit to be off.

After the second circuit is closed, no cI is produced, leading to the third circuit to be on (no repressor at all). And then, kill protein will be produced and kill Nosema Ceranae.

•Positive feedback:

Besides the LuxI and LuxR(which then form a complex called luxR/AHL) produced by first circuit, the third circuit will also produce LuxI and LuxR, which acts as a positive feedback and strongly enhances the production of killer protein.

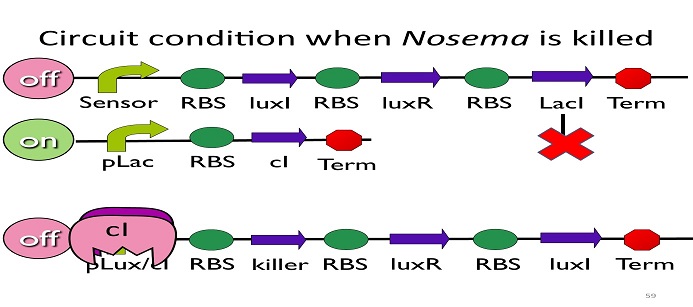
•Circuit condition when Nosema is killed:

After Nosema is killed, the sensor will be off and no lacI will be produced.

Without LacI, the pLac will not be repressed, and the second circuit will be on, leading to the production of cI. After cI binds to pLux/cI hybrid promoter, the third circuit to be off. After that, the overall circuit will switch to the beginning stage when there is no Nosema.

Aims

1. To know how much time it needs from sensing to killing the Nosema after infection

2. To know whether the pathway is effective or not

3. To know the range of kill protein concentration (from the minimal concentration which Is effective to kill Nosema to the maximal concentration which will not do harm to the bees)

It is assumed that AHL is abundant and thus the formation of AHL2LuxR complex is determined only by the concentration of LuxR; CI’s mechanism of binding to the promoter is assumed to act as hill effect form; kill protein will sustain a period of time before it is degraded naturally without any other types of decomposition.

Equations

Equation1:

\frac{d[mRNACI]}{dt}= \frac{1-[LacI]^nLacI}{ KdLacI^nLacI+ [LacI]^nLacI} \times PoPSconstitutive\times\frac{N}{V} -KdegmRNA\times [mRNACI]

KdLacI = dissociation constant of CI

nLacI = Hill coefficient of LacI

PoPSpLac = promoter strength of pLac

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to knowmRNACI production rate and when it can reach the level to translate the desired concentration.

Equation2:

\frac{d[mRNALacI]}{dt}= \frac{1-[ROSoxyR]^nROSoxyR }{ KdROSoxyR ^nROSoxyR + [ROSoxyR]^nROSoxyR} PoPStrxC\times\frac{N}{V}-KdegmRNA[mRNALacI]

KdROSoxyR = dissociation constant ofROSoxyR

nROSoxyR = Hill coefficient of ROSoxyR

PoPStrxC = promoter strength of trxC

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to know how trxC promoter strength (in PoPS) influences the production of lacI.

Equation3:

\frac{d[mRNAOxyR]}{dt}=PoPSconstitutive\times\frac{N}{V}-KdegmRNA\times [mRNAOxyR]

PoPSconstitutive= promoter strength of constitutive promoter (J23102)

N = number of plasmid in a single cell

V = volume of a cell

kdegmRNA = degrading constant of sensor promoter mRNA

The aim of the equation is to know the production rate ofmRNAoxyR, and choose the proper constitutive promoter for boosting OxyR's concentration.

Equation4:

\frac{d[mRNALuxI]}{dt}= \frac{1-[ROSoxyR]^n ROSoxyR }{ Kd ROSoxyR ^n ROSoxyR + [ROSoxyR]^n ROSoxyR I} PoPStrxC\times\frac{N}{V}+\frac{1-[ LuxRAHL]^nLuxRAHL}{ KdLuxRAHL ^nLuxRAHL + [LuxRAHL]^nLuxRAHL}\times\frac{1-{1-[CI leak]^nCI}}{ KdCI^nCI+[CI]^nCI}\times PoPSLuxCI\times\frac{N}{V}-KdegmRNA[mRNALuxI]

KdROSoxyR = dissociation constant ofROSoxyR

nROSoxyR = Hill coefficient of ROSoxyR

PoPStrxC = promoter strength of trxC

KdLuxRAHL = dissociation constant ofLuxRAHL

nLuxRAHL = Hill coefficient of LuxRAHL

KdcI = dissociation constant of CI

ncI = Hill coefficient of CI

PoPSLuxcI = promoter strength of LuxcI hybrid promoter

kdegmRNA = degrading constant of sensor promoter Mrna

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to know how trxC promoter strength (in PoPS) influences the production of LuxI.

Equation5:

\frac{d[mRNALuxR]}{dt}= \frac{1-[ROSoxyR]^n ROSoxyR }{ Kd ROSoxyR ^n ROSoxyR + [ROSoxyR]^n ROSoxyR I} \times PoPStrxC\times\frac{N}{V}+\frac{1-[ LuxRAHL]^nLuxRAHL}{ KdLuxRAHL ^nLuxRAHL + [LuxRAHL]^nLuxRAHL}\times\frac{1-{1-[CI leak]^nCI}}{ KdCI^nCI+[CI]^nCI}\times PoPSLuxCI\times\frac{N}{V}-KdegmRNA[mRNALuxR]

KdROSoxyR = dissociation constant ofROSoxyR

nROSoxyR = Hill coefficient of ROSoxyR

PoPStrxC = promoter strength of trxC

KdLuxRAHL = dissociation constant ofLuxRAHL

nLuxRAHL = Hill coefficient of LuxRAHL

KdcI = dissociation constant of CI

ncI = Hill coefficient of CI

PoPSLuxcI = promoter strength of LuxcI hybrid promoter

kdegmRNA = degrading constant of sensor promoter Mrna

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to know how trxC promoter strength (in PoPS) influences the production of LuxR.

Equation6:

\frac{d[mRNAkill]}{dt}= \frac{1-[ LuxRAHL]^nLuxRAHL}{ KdLuxRAHL ^nLuxRAHL + [LuxRAHL]^nLuxRAHL}\times\frac{1-{1-[CI leak]^nCI}}{ KdCI^nCI+[CI]^nCI}\times PoPSLuxCI\times\frac{N}{V}-KdegmRNA[mRNAkill]

KdLuxRAHL = dissociation constant ofLuxRAHL

nLuxRAHL = Hill coefficient of LuxRAHL

KdcI = dissociation constant of CI

ncI = Hill coefficient of CI

PoPSLuxcI = promoter strength of LuxcI hybrid promoter

kdegmRNA = degrading constant of sensor promoter Mrna

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to knowmRNA of kill protein production rate and when it can reach the level ofthe desired concentration.

Equation7:

\frac{d[Mrnat7]}{dt}= \frac{1-[ROSoxyR]^n ROSoxyR }{ Kd ROSoxyR ^n ROSoxyR + [ROSoxyR]^nROSoxyR }\timesPoPStrxC\times\frac{N}{V}\times {a}+ \frac{1-[T7]^nT7}{ Kd T7^nT7 + [T7]^nT7}\times{PoPST7}\times\ frac{N}{V}-KdegmRNA\times [mRNAT7]

KdROSoxyR = dissociation constant ofROSoxyR

nROSoxyR = Hill coefficient of ROSoxyR

PoPStrxC = promoter strength of trxC

KdT7 = dissociation constant of T7

NT7 = Hill coefficient of T7

PoPST7 = promoter strength of T7 promoter

kdegmRNA = degrading constant of sensor promoter Mrna

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to knowmRNA of T7 polymerase production rate and when it can reach the level to translate enough T7 polymerase.

Equation8:

\frac{d[mRNAPDC]}{dt}=\frac{ [T7]^{nT7} }{ KdT7^{nT7}+[T7]^{nY7} }\times{PoPST7}\times\frac{N}{V}-KdegmRNA\times[mRNAPDC]

KdT7 = dissociation constant of T7

NT7 = Hill coefficient of T7

PoPST7 = promoter strength of T7 promoter

KdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to knowmRNA of enzyme PDC production rate and when it can reach the level to translate enough PDC.

Equation9:

\frac{d[mRNAADH]}{dt}=\frac{ [T7]^{nT7} }{ KdT7^{nT7}+[T7]^{nY7} }\times{PoPST7}\times\frac{N}{V}-KdegmRNA\times[mRNAADH]

KdT7 = dissociation constant of T7

NT7 = Hill coefficient of T7

PoPST7 = promoter strength of T7 promoter

kdegmRNA = degrading constant of sensor promoter mRNA

N = number of plasmid in a single cell

V = volume of a cell

The aim of the equation is to knowmRNA of enzyme ADH production rate and when it can reach the level to translate enough ADH.

Equation10:

\frac{d[CI]}{dt}={RBS}\times{[mRNACI]} -KdegCI\times{[CI]}

RBS = binding site strength

KdegCI = degrading constant of CI

The aim of the equation is to know the production rate of CI and when it can reach the concentration to repress LuxCI hybrid promoter.

Equation11:

\frac{d[LacI]}{dt}={RBS}\times{[mRNA LacI]} - {Kdeg LacI} \times{[LacI]}

RBS = binding site strength

KdegLacI = degrading constant of LacI

The aim of the equation is to knowLacI production rate and when it can reach the concentration to repress promoter LacI.

'Equation12:

\frac{d[LuxI]}{dt}={RBS}\times{[mRNA LuxI]} -KAHL\times{[LuxI]} -Kdeg {[LuxI]} \times{[LuxI]}

RBS = binding site strength

KAHL = LuxI to AHL rate constant

KdegLuxI = degrading constant of LuxI

The aim of the equation is to know the production rate of LuxI concerning the LuxIAHL reaction and LuxI degrading.

'Equation13:

\frac{d[LuxR]}{dt}={RBS}\times{[mRNA LuxR]} – {KmAHL}\times{[AHL]} - {Kdeg LuxR} \times{[LuxR]} \times {KmAHL}\{times[AHL]^{2}} \times{[LuxR]}- KdegAHL\times{[AHL]}

RBS = binding site strength

KmAHL =AHL to LuxI rate constant

KdegLuxR= degrading constant of LuxR

KonAHL = 2AHL + LuxR to (AHL)2/LuxR complex rate constant

KdegAHL = degrading constant of AHL

The aim of the equation is to know the production rate of LuxR concerning the 2AHL + LuxR to (AHL)2/LuxR reaction , AHL to LuxI reaction, and LuxR, AHL degrading.

'Equation14:

\frac{d[AHL]}{dt}={KAHL}\times{[LuxI]}+2\times KoffAHL \times [AHLLuxR] - 2\times KonAHL \times {[AHL]}^{2}\times {[LuxR]} - KdegAHL\times{[AHL]}

KAHL = LuxI to AHL rate constant

KonAHL = 2AHL + LuxR to (AHL)^2/LuxR complex rate constant

KoffAHL = (AHL)2/LuxR complex to 2AHL + LuxR rate constant

KdegAHL = degrading constant of AHL

The aim of the equation is to know the production rate of AHL concerning the LuxIAHL reaction, 2AHL + LuxR to (AHL)2/LuxR reaction, (AHL)2/LuxR complex to 2AHL + LuxR reaction and AHL degrading.

'Equation15:

\frac{d[T7]}{dt}={RBS}\times{[mRNAT7]} –KdegT7\times{[T7]}

RBS = binding site strength

KdegT7 = degrading constant of T7

The aim of the equation is to know the threshold concentration of oxyR to conquer the terminal and when T7 polymerase can reach the required concentration to activate T7 promoter.

'Equation16:

\frac{d[PDC]}{dt}=RBS\times{PoPST7effect}\times\frac{N}{V}-{kdegPDC}\times{[PDC]}

RBS = binding site strength

PoPST7 = promoter strength of T7 promoter

N = number of plasmid in a single cell

V = volume of a cell

KdegPDC = degrading constant of PDC (pyruvate decarboxylase)

The aim of the equation is to know PDC production rate and when it can reach the concentration of ethanol pathway equilibrium.

'Equation17:

\frac{d[ADH]}{dt}=RBS\times{PoPST7effect}\times\frac{N}{V}-{KdegADH}\times{[ADH]}

RBS = binding site strength

PoPST7 = promoter strength of T7 promoter

N = number of plasmid in a single cell

V = volume of a cell

KdegADH = degrading constant of ADH (Acetaldehyde)

The aim of the equation is to know ADH production rate and when it can reach the concentration of ethanol pathway equilibrium.

'Equation18:

\frac{d[AHL]}{dt}=\times KonAHL \times [AHL]^{2}\times{[LuxR]}- {KoffAHL} \times {[AHLLuxR]} - KdegAHL\times{[AHL]}

KAHL = LuxI to AHL rate constant

KonAHL = 2AHL + LuxR to (AHL)2/LuxR complex rate constant

KoffAHL = (AHL)2/LuxR complex to 2AHL + LuxR rate constant

KdegAHL = degrading constant of AHL

'Equation19:

\frac{d[kill]}{dt}={RBS}\times{[mRNAkill]} –Kdegkill\times{[kill]}

RBS = binding site strength

Kdegkill = degrading constant of kill

The aim of the equation is to knowkiller protein production rate and when it can reach the effective concentration to killNosema.

'Equation20:

\frac{d[ethanol]}{dt}=Kpyruvateacetaldehyde\times{Kacetaldehydeethanol}\times\frac{[PDC]^{nPDC} }{ KdPDC^{nPDC}+[PDC]^{nPDC}}\times\frac{[ADH]^{nADH} }{ KdADH^{nADH}+[ADH]^{nADH}}-Km\times\frac{[ADH]^{nADH}}{ KdADH^{nADH}+[ADH]^{nADH}}\times{[ethonal]}

Kpyruvateacetaldehyde = pyruvate→acetaldehyde reaction rate constant

Kacetaldehydeethanol = acetaldehyde→ethanol reaction rate constant

Km = ethanol→acetaldehyde reaction rate constant

KdADH = dissociation constant of ADH

'The aim of the equation is to know ethanol production rate and when it can reach the concentration to kill the spores of Nosema Ceranae.

Explanation:

\frac{d[mRNACI]}{dt}= \frac{1-[LacI]^nLacI}{ KdLacI^nLacI+ [LacI]^nLacI} \times PoPSconstitutive\times\frac{N}{V}-KdegmRNA\times [mRNACI]

In this equation, PoPSpLac represents the promoter strength of LacI promoter, which is measured by the rate of RNApolymerase binding to the starting site of DNA transcription; \frac{1-[LacI]^nLacI }{ KdLacI^nLacI+[LacI]^nLacI } represents the hill effect of repressor LacI to LacI promoter. Because LacI is a repressor, the numerator is {1-[LacI]^nLacI } . For the section of the equation, \frac{1-[LacI]^nLacI}{ KdLacI^nLacI+ [LacI]^nLacI} \times PoPSconstitutive\times\frac{N}{V}represents the synthesizing rate of mRNACI under the influence of LacI and LacI promoter; -{kdegmRNA}\times {[mRNACI]} represents the degrading rate of mRNA

\frac{d[CI]}{dt}={RBS}\times{[mRNACI]} -KdegCI\times[CI]

In this equation, RBS represents ribosome binding site strength, which is the affinity of ribosome to the starting site of mRNA.

For the section of the equation, RBS\times [mRNAcI] represents the synthesizing rate of CI; -{kdegCI}\times {[CI]} represents the degrading rate of CI.

Since LuxCI hybrid promoter is CI dominant, the presence of CI block the promoter and kill protein is not produced. This situation happens when there is no Nosema in bees.

\frac{d[mRNALacI]}{dt}= \frac{1-[ROSoxyR]^nROSoxyR }{ KdROSoxyR ^nROSoxyR + [ROSoxyR]^nROSoxyR} \times {PoPStrxC}\times\frac{N}{V}-KdegmRNA[mRNALacI]

In this equation, PoPStrxC represents the promoter strength of promotertrxC, which is measured by the rate of RNApolymerase binding to the starting site of DNA transcription; \frac{1-[ROSoxyR]^nROSoxyR }{ KdROSoxyR ^nROSoxyR + [ROSoxyR]^nROSoxyR} represents the hill effect of activator ROSoxyR to trxCpromoter.

For the section of the equation, \frac{1-[ROSoxyR]^nROSoxyR }{ KdROSoxyR ^nROSoxyR + [ROSoxyR]^nROSoxyR} \times {PoPStrxC}\times\frac{N}{V} represents the synthesizing rate of mRNALacI under the influence of activator ROSoxyR complex and trxC promoter; -kdegmRNA\times [mRNAlacI] represents the degrading rate of mRNALacI.

\frac{d[LacI]}{dt}={RBS}\times{[mRNA LacI]} –{Kdeg LacI} \times{[LacI]}

In this equation, RBS represents ribosome binding site strength, which is the affinity of ribosome to the starting site of mRNA. For the section of the equation, RBS\times [mRNALacI] represents the synthesizing rate of LacI; -KdegCI\times [LacI] represents the degrading rate of LacI .

LacI will repress pLac promoter, which leads to no production of CI. Without CI, LuxCI hybrid promoter will no longer be repressed, and kill protein can thus be generated. This situation happens when Nosema exists and the sensor promoter is turned on.

\frac{d[mRNAOxyR]}{dt}=PoPSconstitutive\times\frac{N}{V}-KdegmRNA\times [mRNAOxyR]

In this equation, PoPSconstitutive represents the promoter strength of the constitutive promoter J23102, which is measured by the rate of RNApolymerase binding to the starting site of DNA transcription.

For the section of the equation, PoPSconstitutive\times\frac{N}{V} represents the synthesizing rate of mRNA"oxyR" ; -KdegmRNA\times [mRNAOxyR] represents the degrading rate of mRNA"oxyR" .

\frac{d[mRNALuxI]}{dt}= \frac{1-[ROSoxyR]^n ROSoxyR }{ Kd ROSoxyR ^n ROSoxyR + [ROSoxyR]^n ROSoxyR I} \times PoPStrxC\times\frac{N}{V}+\frac{1-[ LuxRAHL]^nLuxRAHL}{ KdLuxRAHL ^nLuxRAHL + [LuxRAHL]^nLuxRAHL}\times\frac{1-{1-[CI leak]^nCI}}{ KdCI^nCI+[CI]^nCI}\times PoPSLuxCI\times\frac{N}{V}-KdegmRNA[mRNALuxI]

In this equation, PoPStrxC,PoPSLuxcI represents the promoter strength of promoter trxC and LuxcI hybrid promoter, which is measured by the rate of RNApolymerase binding to the starting site of DNA transcription; \frac{1-[ROSoxyR]^n ROSoxyR }{ Kd ROSoxyR ^n ROSoxyR + [ROSoxyR]^n ROSoxyR I} represents the hill effect of activator ROSoxyR complex to trxCpromoter; \frac{1-[ LuxRAHL]^nLuxRAHL}{ KdLuxRAHL ^nLuxRAHL + [LuxRAHL]^nLuxRAHL} represents the hill effect of activator LuxRAHL to LuxcI hybrid promoter; \frac{1-[CI leak]^nCI}{ KdCI^nCI+[CI]^nCI} represents the hill effect of repressor CI, while frac{1-{1-[CI leak]^nCI}}{ KdCI^nCI+[CI]^nCI} takes CI leaking into consideration (promoter pLac will not close thoroughly even though CI exists).

For the section of the equation, \frac{1-[ROSoxyR]^n ROSoxyR }{ Kd ROSoxyR ^n ROSoxyR + [ROSoxyR]^n ROSoxyR I} \times PoPStrxC\times\frac{N}{V} represents the synthesizing rate of mRNALuxI under the influence of activator ROSoxyR complex and trxC promoter; \frac{1-[ LuxRAHL]^nLuxRAHL}{ KdLuxRAHL ^nLuxRAHL + [LuxRAHL]^nLuxRAHL}\times\frac{1-{1-[CI leak]^nCI}}{ KdCI^nCI+[CI]^nCI}\times PoPSLuxCI\times\frac{N}{V} represents the synthesizing rate of mRNALuxI under the influence of LuxRAHL complex, CI repression and leaking, and LuxcI hybrid promoter; -kdegmRNA\times [mRNAluxI]represents the degrading rate of mRNAluxI.

\frac{d[LuxI]}{dt}={RBS}\times{[mRNA LuxI]} -KAHL\times{[LuxI]} -Kdeg {[LuxI]} \times{[LuxI]}

In this equation, RBS represents ribosome binding site strength, which is the affinity of ribosome to the starting site of mRNA; KAHL represents the rate constant of AHL to LuxI. For the section of the equation, {RBS}\times {[mRNALuxI]} represents the synthesizing rate of LuxI; KAHL[LuxI] represents the transforming rate of AHL to LuxI; -KdegLuxI\times [LuxI] represents the degrading rate of LuxI.

In this equation, PoPStrxC,PoPSLuxcI represents the promoter strength of promoter trxC and LuxcI hybrid promoter, which is measured by the rate of RNApolymerase binding to the starting site of DNA transcription; \frac{1-[ROSoxyR]^n ROSoxyR }{ Kd ROSoxyR ^n ROSoxyR + [ROSoxyR]^n ROSoxyR I} represents the hill effect of activator ROSoxyR complex to trxCpromoter; \frac{1-[ LuxRAHL]^nLuxRAHL}{ KdLuxRAHL ^nLuxRAHL + [LuxRAHL]^nLuxRAHL} represents the hill effect of activator LuxRAHL to LuxcI hybrid promoter; \ frac{1-[CI leak]^nCI}{ KdCI^nCI+[CI]^nCI} represents the hill effect of repressor CI, while frac{1-{1-[CI leak]^nCI}}{ KdCI^nCI+[CI]^nCI} takes CI leaking into consideration (promoter pLac will not close thoroughly even though CI exists).

For the section of the equation, \frac{1-[ROSoxyR]^n ROSoxyR }{ Kd ROSoxyR ^n ROSoxyR + [ROSoxyR]^n ROSoxyR I} \times PoPStrxC\times\frac{N}{V} represents the synthesizing rate of mRNALuxR under the influence of activator ROSoxyR complex and trxC promoter; \frac{1-[ LuxRAHL]^nLuxRAHL}{ KdLuxRAHL ^nLuxRAHL + [LuxRAHL]^nLuxRAHL}\times\frac{1-{1-[CI leak]^nCI}}{ KdCI^nCI+[CI]^nCI}\times PoPSLuxCI\times\frac{N}{V} represents the synthesizing rate of mRNALuxR under the influence of LuxRAHL complex, CI repression and leaking, and LuxcI hybrid promoter; -kdegmRNA\times [mRNAluxI]represents the degrading rate of mRNAluxR.

\frac{d[LuxR]}{dt}={RBS}\times{[mRNA LuxR]} – {KmAHL}\times{[AHL]} - {Kdeg LuxR} \times{[LuxR]} \times {KmAHL}\{times[AHL]^{2}} \times{[LuxR]}- KdegAHL\times{[AHL]}

In this equation, RBS represents ribosome binding site strength, which is the affinity of ribosome to the starting site of mRNA; KmAHL represents the rate constant of AHLLuxI; KonAHL represents the rate constant of 2AHL+LuxR to AHL2LuxR complex.

For the section of the equation, { RBS}\times{ [mRNALuxR]} represents the synthesizing rate of LuxR; { -KmAHL}\times{ [AHL]} represents the transforming rate of AHL to LuxI; {-KdegLuxR}\times {[LuxR]} represents the degrading rate of LuxR; { -KonAHL}\times{ [AHL]^2}\times{ [LuxR]} represents the transforming rate of 2AHL+LuxR to AHL2LuxR complex; {-KdegLuxI}\times {[AHL]} represents the degrading rate of AHL.

\frac{d[AHL]}{dt}={KAHL}\times{[LuxI]}+2\times KoffAHL \times [AHLLuxR] - 2\times KonAHL \times {[AHL]}^{2}\times {[LuxR]} - KdegAHL\times{[AHL]}

In this equation, KAHL represents the rate constant of AHL to LuxI; KoffAHL represents the rate constant of AHL2LuxR complex to 2AHL+ LuxR, while KonAHL represents the reverse rate constant.

For the section of the equation, {KAHL}\times {[LuxI]} represents the transforming rate of LuxI to AHL; {2}\times {KoffAHL}\times{ [AHLLuxR]} represents the transforming rate of AHL2LuxR complex to AHL and LuxR, the constant 2 means that each complex turns into two AHL; -{2}\times {KonAHL}\times {[AHL]^2}\times {[LuxR]} represents the transforming rate of 2AHL+LuxR to AHL2LuxR complex; {-KdegLuxI}\times {[LuxI]} represents the degrading rate of LuxI.

Since LuxI will transform to AHL, and 2AHL will combine to LuxR to form AHL2LuxR complex. Because AHL2LuxR will then bind to LuxCI hybrid promoter and activate kill gene, LuxR gene, and LuxI gene. In this way, kill protein will kill Nosema, while LuxR, LuxI will trigger the positive feedback and enhance the production of kill protein.

\frac{d[kill]}{dt}={RBS}\times{[mRNAkill]} –Kdegkill\times{[kill]}

After trxC promoter is turned on by ROSoxyR complex and the downstream genes – LacI, LuxI, and LuxR starts to produce, which blocks the CI promoter and turns on the LuxCI hybrid promoter. After that, the gene encoded with kill protein downstream LuxCI hybrid promoter also begins to transcribe.

This equation shows production rate of mRNAkill. PoPSLuxcI represents the promoter strength of promoter trxC and LuxcI hybrid promoter, which is measured by the rate of RNApolymerase binding to the starting site of DNA transcription; \frac{1-[ LuxRAHL]^nLuxRAHL}{ KdLuxRAHL ^nLuxRAHL + [LuxRAHL]^nLuxRAHL} represents the hill effect of activator LuxRAHL to LuxcI hybrid promoter; \ frac{1-[CI leak]^nCI}{ KdCI^nCI+[CI]^nCI} represents the hill effect of repressor CI, while frac{1-{1-[CI leak]^nCI}}{ KdCI^nCI+[CI]^nCI} takes CI leaking into consideration (promoter pLac will not close thoroughly even though CI exists).

For the section of the equation, \frac{1-[ LuxRAHL]^nLuxRAHL}{ KdLuxRAHL ^nLuxRAHL + [LuxRAHL]^nLuxRAHL}\times \frac {1-[CI leak]^nCI}{ KdCI^nCI+[CI]^nCI}\times {PoPSLuxcI} \times \frac{N}{V}

represents the synthesizing rate of mRNAkill under the influence of LuxRAHLCI repression and leaking, and LuxcI hybrid promoter; -kdegmRNA\times [mRNALuxR] represents the degrading rate of mRNAkill.

As for explanations of equation7, 8, 9, 15, 16, 17, 20, please see the ethanol wiki for more information.

Results:

After Nosema invasion (t=0), concentration of kill protein will reach its constant level, which is 6.5\times 10^(-9)M. The effective concentration of kill protein to kill Nosema is 6.7\times 10^(-10)M, which is near the level we have modeled. Besides, the time to reach this concentration is 24 hours after Nosema invasion. Since three days after Nosema invasion, bees will start to spread Nosema, the constant level of kill protein (which is a little higher than the effective one)and the time it needs to reach this level (which is a little bit shorter than )shows that Bee. Coli can save the bees timely.

Similarly, the effective concentration of ethanol to kill bees is 2.4\times 10^(-6)M and the time to reach this concentration is 72 hours after Nosema invasion. Since kill protein will kick on two days after Nosema invasion, the open time of ethanol (four days after Nosema invasion) is what we desired. That is, because ethanol is the last end of preventing Nosema from spreading (it kills the infected bees as well), we want the open time of ethanol to be later than kill protein open time.

The benefits of our circuit are that the dissociation constant of T7 (KdT7) is small, which means it is sensitive (will swiftly open right after T7 polymerase reaches threshold) and that we use positive feedback to attain the goal of open this device like a switch.

Parameters:

Model	Parameter	Description	Value	Unit	Reference
Sensor	KdegOxyR	OxyR degrading rate	10⁷	M^-1 x min^-1	Regulation of the OxyR transcription factor by hydrogen peroxide and the cellular thiol—disulfide status
	KdOxyR*	Dissociation constant of OxyR*	10^-7.33	M
	KOxyR	OxyR producing rate constant	5.012 x 10¹⁴	X
	nOxyR*	Hill coefficient of OxyR*	Ranging from 0.75~3.5,depends on what kind of ROS it react with	X	OxyR: A Molecular Code for Redox-Related Signaling
	N	Copy number	887(cells containing 25％ plasmid bearing cells)	Single piece	Escherichia coli Plasmid Copy Number Assay Improved determination of plasmid copy number using quantitative real-time PCR for monitoring fermentation processes
Ethanol	pyruvate	Initial concentration of pyruvate in MG1655	1.18 x 2	g/L	Expression of pyruvate carboxylase enhances succinate production in Escherichia coli without affecting glucose uptake
	nPDC	Hill coefficient of PDC	2.1	-	Purification, characterization and cDNA sequencing of pyruvate decarboxylase Zygosaccharomyces biporus
	nADH	Hill coefficient of ADH	at high pH values, 30◦C, n=1; at low temperature, n=3	-	Evidence for co-operativity in coenzyme binding to tetrameric Sulfolobus solfataricus alcohol dehydrogenase and its structural basis: ﬂuorescence, kinetic and structural studies of the wild-type enzyme and non-co-operative N249Y mutant
SEIR(exponential)	b	Infection rate constant of Nosema ceranae to the suspected	24/75	Period(days)-1
	r1	Infection rate constant of K12 to the suspected	3/20	Period(days)-1	1. Environment protection administration executive yuan of R.O.C Medical bacteriology of J.A.T
	r2	Infection rate constant of K12 to the latent	3/20	Period(days)-1	2. Environment protection administration executive yuan of R.O.C. 3. Medical bacteriology of J.A.T
	e	rate of the latent turns infectious	1/4	Period(days)-1
	u	Death rate of the infected	1/8	Period(days)-1
	k	Rate of intaking capsule	24/11	Period(days)-1
SEIR(exponential&linear)	S	x(1)	Amount of total population
	E	x(2)	Amount of suspected individuals
	I	x(3)	Amount of individuals in the latent period
	R	x(4)	Amount of infected individuals

Retrieved from "http://2013.igem.org/Team:NYMU-Taipei/Modeling/MainParts"

@@ Line 286: / Line 286: @@
 <html>
 <div lang="latex" class="equation">
-\frac{d[LacI]}{dt}={RBS}\times{[mRNA LacI]} -Kdeg LacI \times{[LacI]}
+\frac{d[LacI]}{dt}={RBS}\times{[mRNA LacI]} - {Kdeg LacI} \times{[LacI]}
 </div>
 </html>

Team:NYMU-Taipei/Modeling/MainParts

From 2013.igem.org

Revision as of 13:33, 21 October 2013

Contents

main part

Function of the parts:

Aims

Equations

Explanation:

Results:

Parameters: