Sensor Model

Introduction

In order to determine our Iron Coli's enterobactin production rate, we first have to know how much time our bacteria will take to sense the ambient iron. So, this first part of the Enterobactin production model focuses on the synthetic sensing system our team implemented in the bacteria.

Observations

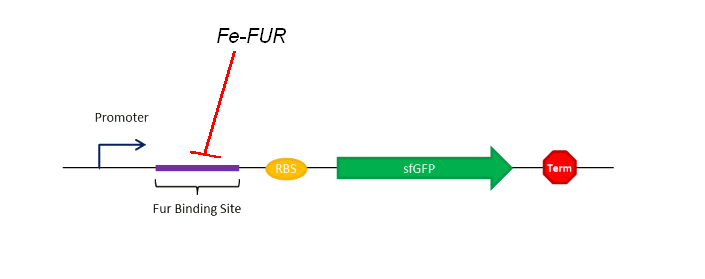
As shown on the Figure 1, our sensing system relies on a FUR Binding Site (FBS). In order to easily model the sensing delay and analyse its results, the first construction is composed of a GFP placed right after the FBS.

Figure 1: Our first construction, our Iron sensor system

See our sensor page for more details

Goals

Our goal in this part of the model is to create a generic FBS-related sensing model so that:

• We can determine the iron-sensing delay of our bacteria
• The model can can be reused by other iron related projects

Materials and methods

From Iron to FBS:
The iron-FUR complex is simply formed that way:
 
We reduced this equation to:

Which is not annoying, since we just have to divide our [FeFur] by two to get the real complex concentration.
We can easily write down both the formation (v) and the dissociation (v') speeds:

We chose to model the iron input in the bacteria using a linear function of the external iron concentration Ferext, the factor p being the cell-wall permeability for iron.
The FUR on the other hand is produced by the bacteria. Its evolution can also be considered as linear, using a mean production rate of Fur0.

In this model, we only track the free Fe-FUR complex and not those attached to a FUR Binding Site. FBS is the number of inhibited Fur Binding Sites.

GFP expression:
To simulate the inhibition phenomenon, we chose to use our Logistic function under its differential form. Since it is the Fe-FUR that represses it, the LacI can be expressed as a logistic fuction of the Fe-FUR:

K_i1 is a non-dimensional parameter that repesents the inhibition power, and K_f is the fixation rate of the Fe-FUR on the FBS. Finally, N_pla1 is the number of pasmids containing the GFP.

GFP Production:
The [mRNA] and [GFP] equations are alike. The prodction rates are Kr for the mRNA and Kp for the GFP, and both variables have a negative degadation term:

Results

Conclusion

Models and scripts