Mathematical Modeling of Bistable Toggle Switch

Cooperativity

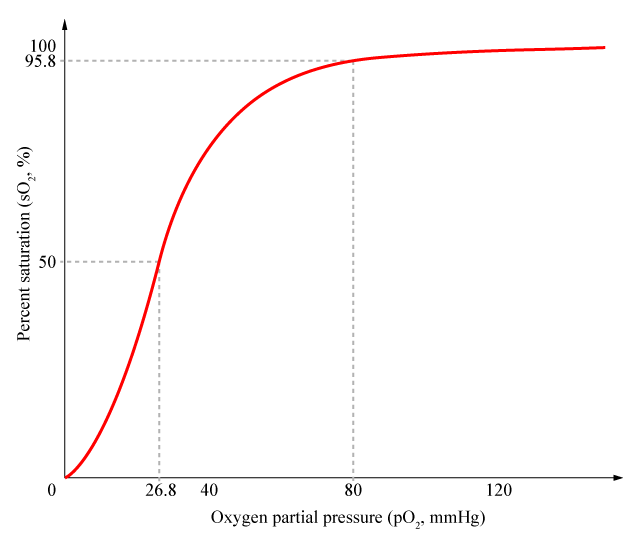
Cooperativity is a common phenomenon in biological systems involving multiple ligands binding to enzymes or receptors. The change in affinity of a binding site for a ligand upon a ligand-binding leads to either positive cooperativity in which affinity is increased and subsequent binding become more likely, or negative cooperativity in which affinity is decreased to hinder future binding. One of the most famous examples of cooperative binding is the binding of oxygen to hemoglobin, the oxygen-transporting protein in red blood cells. When an oxygen molecule bind to hemoglobin, its affinity for oxygen increases greatly, and when three oxygen molecules bind (3-oxy-hemoglobin), its affinity for the fourth one is nearly three-hundred times higher than deoxy-hemoglobin’s affinity for oxygen. This cooperative property leads to the sigmoidal shaped curve shown below.

It has been shown by both mathematical derivation and experimental data that proteins that form multimers have cooperativity. A transcriptional repressor of the lac operon, lacI proteins form tetramers and show cooperative repression of transcription. Similarly, tetracycline repressor (tetR) found in E.coli form dimers, and as a result show cooperativity. Professors Hermann Bujard and Manfred Gossen from University of Heidelberg developed a synthetic transcription factor called Tet-On and Tet-Off using this naturally found tetR respressor. By fusing VP16 activator found in Herpes Simplex Virus with tetR, they were able to make synthetic repressors (tetracycline transactivator, tTA) that could target specific locations named TetO operator sequences.

In addition to multimerization, combinatorial promoter binding has been shown to generate cooperativity. Having multiple operator sites for both inducers and repressors produced cooperative response and it is this design that we chose to use in our project (with multiple binding sites for iTALs and CRISPR-Cas9). Cooperativity of repressors with multiple binding sites will be further explored in our mathematical models.

Hill Equation

Named after English physiologist Archibald Vivian Hill who studied the sigmoidal binding curve of hemoglobin, the Hill Equation provides a way to quantify cooperativity. The equation describes the fraction of proteins or enzymes that are saturated by ligands as a function of the concentration of ligands.

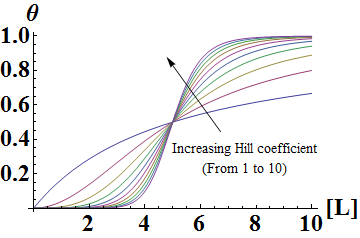
In the Hill Equation shown above, theta represents the fraction of binding sites occupied by ligands, [L] is the ligand concentration, n is the Hill coefficient, and Kd is the dissociation constant of the ligand. The value of the Hill coefficient describes the cooperativity of ligand binding: n>1 for positive cooperativity, n<1 for negative cooperativity and n=0 for no cooperativity. The above equation can also be applied to cooperative induction or activation of transcription, where theta represents the level of mRNA produced and [L] represents the level of inducer present. More cooperative the activation is, the steeper the slope will be, and the expression of the gene becomes more switch-like with distinct on and off states without intermediate states. Shown below is the graph the of Hill equation with various Hill coefficients. As one can see, increasing the Hill coefficient makes the change (induction) more abrupt and switch-like.

References

1. Bujard et al., "Tight Control of Gene Expression in Mammalian Cells by Tetracycline-Responsive Promoters.". Proc. Natl. Acad. Sci. U.S.A. 89 (12): 5547–51. (1992)
2. Allen et al., "Directed Mutagenesis in Embryonic Stem Cells". Mouse Genetics and Transgenics: 259–263. (2000)
3. Bintu et al., "Transcriptional regulation by the numbers". Current Opinion in Genetics and Development. 15, pp. 116-124 (2005)
4. Murphy et al., "Combinatorial promoter design for engineering noisy gene expression". PNAS. 104(13), 12726-12731. (2007)