"

From 2013.igem.org

iGEM Home

Contents 1 Modeling Objectives: 1.1 Assumptions: 1.2 Bacteria Growth: 1.3 Viral Growth 1.4 Substrate utilization 1.5 Model Validation 1.6 Product Formation 1.7 Co-culture: Numerical Model 1.8 Co-culture: Computational Model

Modeling Objectives:

1. Predict the growth of recombinant E. coli cultures under phage predation.
2. Predict caffeine production based on initial starting number of viruses, (ie. multiplicity of infection; MOI).

Assumptions:

1. Bacteria is grown in a batch culture and follows the Monod growth equation.
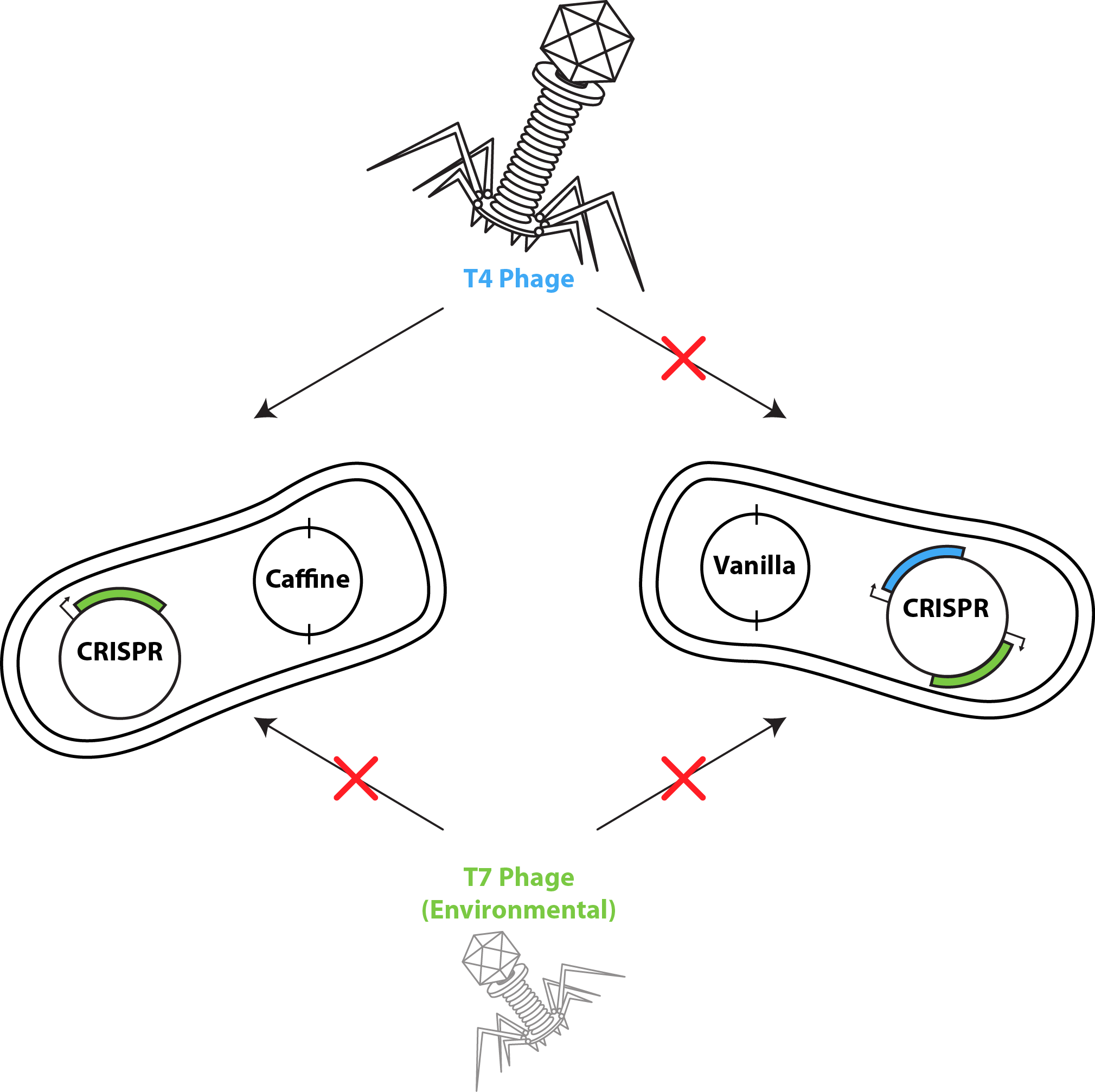
2. Bacteria with the CRISPR are nearly 100% immune to the specific phage infection.
3. Bacteria without CRISPR system are completely susceptible to phage infection.
4. Yield coefficients and phage attachment coefficients are constants.
5. Bacterial phages do not decrease significantly in number during the course of an experiment.
6. All considered bacterial phages are lytic.

Bacteria Growth:

We begin with a populations balance for a given strain $X$, \begin{align} \frac{dX}{dt} = \frac{dX_i}{dt} + \frac{dX_u}{dt} \end{align} The infected bacteria is represented by $X_i$, uninfected bacteria by $X_u$ and $X = X_i + X_u$. We use the Monod equation to model the substrate limited bacterial growth. \begin{align} \mu_{X} = \mu_{max, X} \frac{S}{K_{S, X} + S} \end{align}

Where $\mu_{X}$ is the bacterial growth rate, $\mu_{max, X}$ is the maximum bacterial growth rate, $S$ is the growth limiting substrate and $K_s$ is the amount of substrate remaining when the growth rate is half of maximum. Due to environmental factors, some bacteria will die; the death rate ($k_d$) is assumed to be directly proportional to the bacteria population. A lag phase is modelled by multiplying a dampening term to the growth rate, namely $(1 - e^{-\alpha t})$, where $\alpha$ is defined as a proportionality constant. The slowing of growth from exponential to stationary is modelled with yet another dampening term to be multiplied to the growth: $exp\big[{-\big(\frac{X}{X_c}\big)^m\big]}$. This dampening term is related to the quorom sensing in bacteria, once the bacteria reach some characteristic concentration ($X_c$) the bacteria begin to slow down growth. Thus the uninfected cell growth is described by: \begin{align} \frac{dX_u}{dt} = \big( \mu_{X, u}e^{-\big(\frac{X}{X_c}\big)^m} - k_{d_{X,u}} \big) X_u\big(1 - e^{-\alpha t}\big) \end{align} For clarity, in this model, $m$, $X_c$, and $\alpha$ are all to be empirically determined and assumed constant. In reality, each constant is dependent on many variables, for example: $\alpha(temperature, pressure, [substrate], environmental \ conditions, bacterial \ strain, more)$. Similarly for infected cells: \begin{align} \frac{dX_i}{dt} = \big( \mu_{X, i}e^{-\big(\frac{X}{X_c}\big)^m} - k_{d_{X,i}} \big) X_i\big(1 - e^{-\alpha t}\big) - \delta \end{align}

However, a major difference is that the decay rate for the infected cells is dependent on the latency time of the virus and thus we introduce $\delta$. The function $\delta$ is defined as follows, \begin{align} \delta = &N(\tau)X_i , \ \ during \ lysis\\ & 0, \ \ \ \ \ \ \ \ \ \ \ \ \ otherwise \end{align} Here $N(\tau)$ is a normal distribution over some time $\tau$, in other words, it is expected that the infected population will lyse according to a normal distribution over the domain $(-\tau, \tau)$.

Viral Growth

It is now necessary to consider the phage population $V$ as it directly affects the amount of bacteria that are infected at any given time. To describe the phage population it is necessary to consider how many phages are released per cell lysis, this number is referred to as the burst size $(\beta)$. \begin{align} V = V_0 + X_i \beta ^{\frac{t}{LT}} \end{align} Where $V_0$ is the initial phage populations and $LT$ is the latency time (they time between infection and lysis). However, since lab techniques are tricky to measure the exact phage at various time points as well as the exact amount of infected bacteria, it is desired to simplify the model. It is reasonable to use a stepwise function that describes the amount of free phage present. Also, since the burst size is large, on the order of $100$, we see that the loss of current phage due to infection of cells is small (roughly 1%), thus to simplify computations we consider this to be negligible. With these deductions we arrive at the following: \begin{align} V = V_0 + E(X_i)\beta^{\big[\frac{t}{LT}\big]} \end{align} Where $E(X_i)$ is the expected infected population and $\big[\frac{t}{LT}\big]$ is the largest integer equal or less than $\frac{t}{LT}$. To find the expected infected population, the Poisson distribution is used based on the MOI. However, there is an efficiency of viral attachment $\epsilon \in (0, 1)$ (in fact the efficiency has been found to be a function of certain proteins [reference]). \begin{align} MOI = \frac{V}{X} \end{align}

\begin{align} E(X_i) = \epsilon X(1 - e^{-MOI}) \end{align}

Substrate utilization

The bacteria will need to use a substrate, and the depletion of this substrate is proportional to the growth of the uninfected bacteria and the amount of bacteria. Although the infected bacteria do not multiply when infected, the infected cells may use up substrate to gain the energy needed to replicate the phage. Although it may be the case that the bacteria simply recycle intracellular material, a substrate utilization term ($\gamma$) for the infected cells is utilized (if the bacteria do in fact recycle intracellular material, it follows that this value will be 0). Moreover, when cells lyse, the cell materials can be metabolized by other bacteria and will add to the amount of nutrients available. Thus, the equation for substrate utilization rate is:

\begin{align} \frac{dS}{dt} = - \big[ \frac{\mu_u}{Y_u}X_u + \frac{\gamma}{Y_i}X_i \big] + \phi \delta \end{align} Where $Y_u$ and $Y_i$ are yield constants and $\phi$ is the average amount of substrate released per infected cell during lysis. For clarity, $\delta$ is as described above.

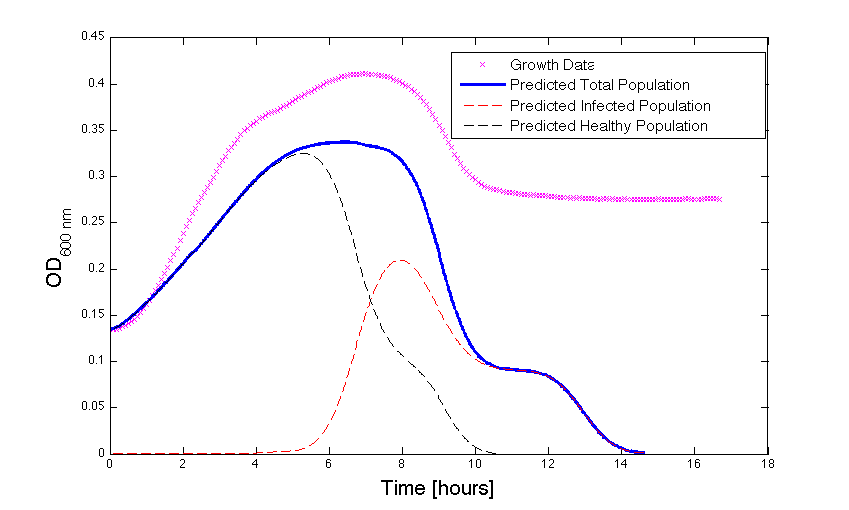
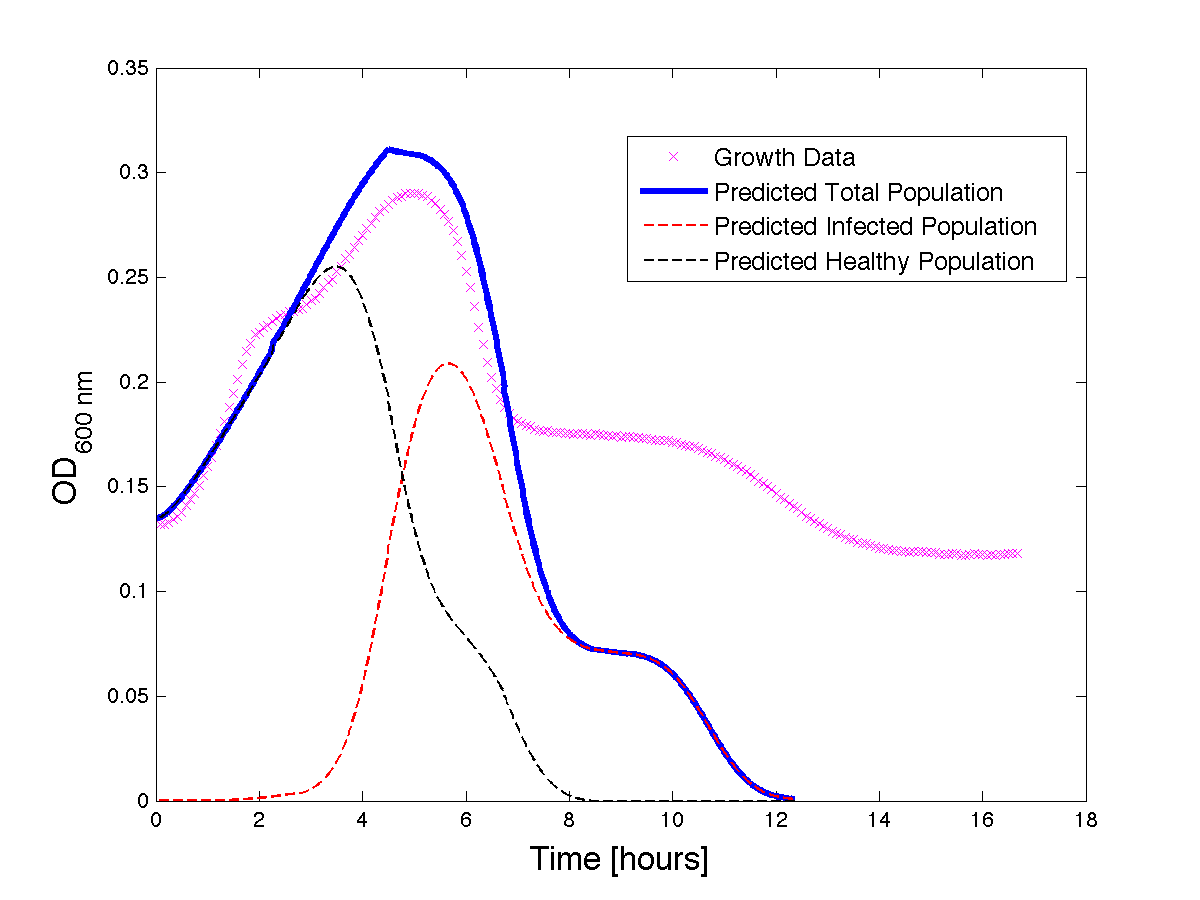
Model Validation

Although, only limited amounts of growth curves have been able to be analyzed, the initial quantitative results appear promising and the qualitative results appear to have value as well. For the curves that did not match quantitatively, the qualitative curve was still good at predicting culture collapse (bear in mind that OD measurements will contain "bacterial bones" which will artificially inflate the concentration of bacteria upon lysis)

Product Formation

For a given uninfected bacteria $X_u$ that can produce the product $P$, we will first expect the production rate to be first order equation: \begin{align} \frac{d[P]}{dt} = \mu_{X_u} [P]X_u \end{align} For infected bacteria we expect the product formation rate to be negligibly small.

Co-culture: Numerical Model

The end goal of our project is to tune product formation by adding phage to a batch reactor at the same time as having one flavour in constant production. Thus, we must model a two culture system. Let our bacterial cultures be called $X$ and $Z$. Let Z be immunized to the phage with our CRISPR system. Our equations become \begin{align} &\frac{dX}{dt} = \frac{dX_i}{dt} + \frac{dX_u}{dt} \\ &\frac{dZ}{dt} = \frac{dZ_i}{dt} + \frac{dZ_u}{dt} \\ &\frac{dX_u}{dt} = \big( \mu_{X, u}e^{-\big(\frac{X}{X_c}\big)^m} - k_{d_{X,u}} \big) X_u\big(1 - e^{-\alpha t}\big) \\ &\frac{dZ_u}{dt} = \big( \mu_{Z, u}e^{-\big(\frac{Z}{Z_c}\big)^m} - k_{d_{Z,u}} \big) Z_u\big(1 - e^{-\alpha t}\big) \\ &\frac{dX_i}{dt} = \big( \mu_{X, i}e^{-\big(\frac{X}{X_c}\big)^m} - k_{d_{X,i}} \big) X_i\big(1 - e^{-\alpha t}\big) - \delta\\ &\frac{dZ_i}{dt} = 0\\ &\frac{dS}{dt} = - \big[ \frac{\mu_{X_u}}{Y_u}X_u + \frac{\gamma_X}{Y_i}X_i + \frac{\mu_Z}{Y_Z}Z\big] + \phi \delta \\ &\frac{dP_X}{dt} = \frac{\mu_X}{Y_{P_X}}X_u\\ &\frac{dP_Z}{dt} = \frac{\mu_Z}{Y_{P_Z}}Z_u \end{align} Subject to conditions: \begin{align} &X(0) = X_0\\ &Z(0) = Z_0\\ &Z_i(t) = 0\\ &S(0) = S_0\\ &S(t) = S_t\\ &P_X(0) = 0\\ &P_Z(0) = 0\\ &X = X_i + X_u\\ &X_i = E(X_i) = \epsilon X(1 - e^{-MOI})\\ &OD(t) = OD_Z(t) + OD_X(t) \end{align}

Co-culture: Computational Model

For the computational model of co-cultures we used the software gro by washington...

Please insert grow movie here....