Team:TU-Munich/Modeling/Kill Switch

From 2013.igem.org

Revision as of 14:21, 27 October 2013 by ChristopherW (Talk | contribs)

(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)

Kill Switch Modeling

Purpose

The idea of our kill switch is to kill off our moss, as soon as it leaves the filter system. For this purpose two methods were proposed:

siRNA method: When some trigger is activated, siRNA is expressed inhibiting the expression of a vital gene
nuclease method: When some trigger is activated, a nuclease is released destroying the DNA of the cell

To decide between these two methods we modelled the vitality V of the cell (a number between 0 and 1, so a perfectly functional cell has V=1, a dead cell V=0) and depending on the tested method the concentration of siRNA R and nuclease N as appropriate. Both concentrations are normalized to the unit interval [0,1].

siRNA Model

Governing equations

Figure 2: Simulation of pollutant concentration with freely diffusiable cell wall and no enzymes

Figure 1: Example solution to our siRNA model with parameters k₁=1, k₂=2, k₃=2, k₄=1.

We determined the governing equations of this model to be the following:

with initial conditions V(0) = 1 and R(0) = 0, where at the time t=0 the trigger is activated.

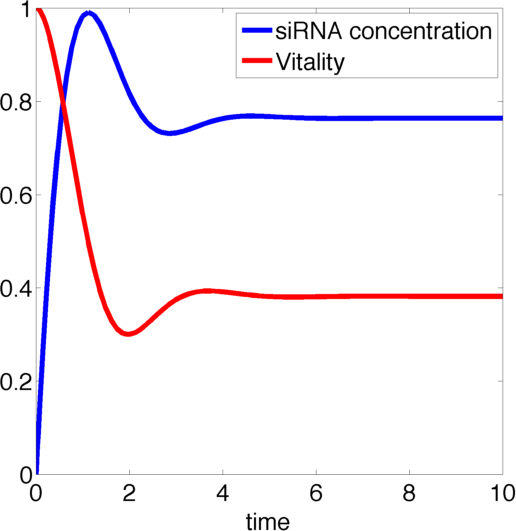
Figure 1, created by our MatLab script siRNA model shown below, on the right shows a solution to this system for some example parameters. In this case the vitality of the cell decreases to somewhere around 0.3 while at the same time after an initial peak the siRNA concentration also drops upon which the vitality settles in at about 0.4.

So it appears, that the siRNA approach does not achieve the required death of the cells. In the following it will be shown, that this is the case for all parameter values.

Calculation of stable points and analysis

The steady points V* and R* of this system have to satisfy

Defining

we get the following quadratic equation for the steady point of V

If α = 1, the unique steady point is .

To analyze the stability of these the eigenvalues of the Hessian matrix H

must be computed. The eigenvalues are

These are both negative, so this is a stable point, i.e. an attractor.

If α ≠ 1, the steady points are

Now only one of these is in the sensible range, because

for α > 1:
for α < 1:

So there is only one steady point in this range, namely:

By expanding the fraction by we can rewrite V* as

So using the results from above, we get:

Now look at the eigenvalues of the Hessian matrix to analyze the stability

Defining , the eigenvalues are given by

So , which means that this is a stable attractor.

Result of our model

So for the siRNA there always is a stable point for the vitality between (but excluding) 0 and 1, so the moss is not killed-off completely, just impeded in its growth.

Interpretation

This result makes intuitive sense, because as the function of the cell is repressed the cell produces less of the inhibiting siRNA, which leads to a regeneration of the cell. Eventually a steady state at a lower vitality is reached, where the vitality stays constant.

Stochastic Model

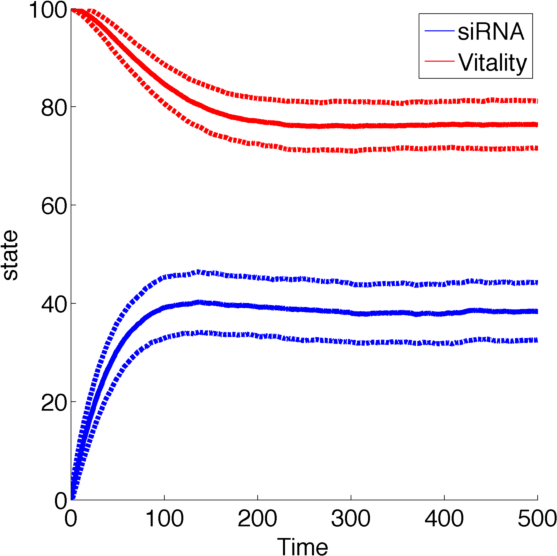
Figure 2: Averaging over 1000 realisations of the Gillespie algorithm. Solid line indicates the mean, dashed lines indicate the 1-σ interval.

As number of siRNA in a cell can be very small, we cannot always assume that there is an sufficient amount of RNA such we can rule out stochastic effect. To deal with this problem we set up an analogous stochastic model constisting of a Markov Jump Process of the two species with a total of 4 reactions.

The state space [0,1] was discretised to [1,2,3,...,100] for both species R and N while the reaction rates were kept the same.

To simulate the model we used and implementation of the Gillespie Algorithm with 1000 realisations and then averaged over all realisations.

With this implementation the qualitative behaviour of the system remains unchanged, while the quantitative changes which is due to the discretization.

Nuclease Model

Governing equations

Figure 3: Example solution to our nuclease model with parameters p₁=1, p₃=0.5, p₄=0.005.

We determined the governing equations of this model to be the following:

with initial conditions V(0) = 1 and N(0) = 0, where at the time t=0 the trigger is activated.

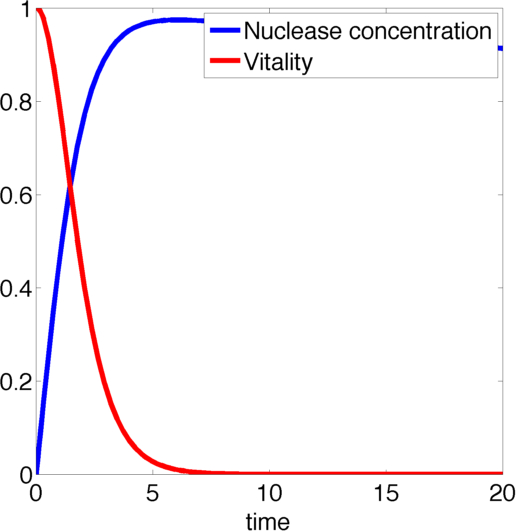
Figure 2, created by our MatLab script nuclease model shown below, on the left shows a solution to this system for some example parameters. It clearly shows that in this case the vitality of the cell decreases to 0 and remains there, i.e. that the cell has died.

In the following we will verify, that this is the case for all parameter values.

Calculation of stable points and analysis

Any steady state given by V* and N* of this system must to satisfy

The Hessian matrix of this system for the steady point is easy to solve

The eigenvector corresponding to the zero eigenvalue is . It is obvious from the equations that any disturbance away from the steady state along this vector will decay back to the steady state, so this is a stable attractor.

Results of our model

The nuclease always reduces the vitality of the moss to 0, i.e. kills it off completely.

Interpretation

Again this result is very intuitive, since the moss cannot regenerate from the destruction of its genome.

Conclusions

For a functional kill-switch it is necessary, that the cells are actually killed and not just live on with reduced vitality. So based on our modeling results the siRNA approach is not satisfactory, while the nuclease satisfies the requirement. As a result the team pursued the nuclease approach leading to our final kill-switch.

MatLab Scripts

siRNA model script

% f = @(R,V,k) [k(3)* V  - k(4) * R , -k(1) * R * V + k(2) *(V  -1)* (R  -1)];
g = @(k,y)    [k(3)* y(2)- k(4)*y(1); -k(1)*y(1)*y(2)+k(2)*(y(2)-1)*(y(1)-1)];

%k= [  k1,  k2,  k3,  k4 ]; %insert the appropriate reaction rate constant
k = [   1,   2,   2,   1];

[TOUT, YOUT] = ode45(@(t,y) g(k,y) ,[0,10],[0;1]);

plot(TOUT, YOUT(:,1), 'markersize', 15, 'linewidth', 5)
hold on; plot(TOUT, YOUT(:,2), 'r', 'markersize', 15, 'linewidth', 5); hold off

legend('siRNA concentration','Vitality');
xlabel('time');
set(gca,'FontSize',24);
set(gcf,'position', [100 100 600 600]);

axis square
set(gcf,'Color','w');
export_fig siRNA_pic.png

Stochastic siRNA script

%% 1 States
% [R,V]
x0 = [0,100];

%% 2 Reactions
% stoichiometric matrix
S = zeros(4,2);

%% 2.1 increase siRNA
% R -> R + 1
% rate k3 * V
S(1,:) = [1,0];

%% 2.2 degrade siRNA
% R -> R - 1
% rate k4 * R
S(2,:) = [-1,0];

%% 2.3 increase vitality
% V -> V + 1
% rate k2 * ( V - 1 ) * ( R - 1 )
S(3,:) = [0,1];

%% 2.4 decrease vitality
% V -> V - 1
% rate k1 * R * V
S(4,:) = [0,-1];


param = [   1,   2,   1,   2];

% rates
acell = { @(t,x,k) k(3) * x(2)/100,
    @(t,x,k) k(4) * x(1)/100,
    @(t,x,k) k(2) * ( x(2) - 100 )/100 * ( x(1) - 100 )/100,
    @(t,x,k) k(1) * x(1) * x(2)/100};

a = @(t,x,k) [feval(acell{1},t,x,k),feval(acell{2},t,x,k),feval(acell{3},t,x,k),feval(acell{4},t,x,k)];

% time vector

N_time = 100;

tt = linspace(0,100,N_time);

% number of runs
N_repeat = 1000;

% output
X_runs = zeros(N_repeat,N_time,length(x0));


%plotting
figure(1)
clf
hold on

for j = 1:N_repeat 
    [X_runs(j,:,:)]=SSA(x0,S,a,tt,param);
end

figure
hold on
plot(tt,mean(X_runs(:,:,1)),'b')
plot(tt,mean(X_runs(:,:,2)),'r')
legend('siRNA','Vitality')
for k = 1:length(x0)
    switch k
        case 1
        plot(tt,mean(X_runs(:,:,k)),'b')
        plot(tt,mean(X_runs(:,:,k))+sqrt(var(X_runs(:,:,k))),'--b')
        plot(tt,mean(X_runs(:,:,k))-sqrt(var(X_runs(:,:,k))),'--b')
        case 2
        plot(tt,mean(X_runs(:,:,k)),'r')
        plot(tt,mean(X_runs(:,:,k))+sqrt(var(X_runs(:,:,k))),'--r')
        plot(tt,mean(X_runs(:,:,k))-sqrt(var(X_runs(:,:,k))),'--r')
    end
end

find(X_runs(:,:,2)==0,1,'first')
set(gcf,'Color','w')
axis square
export_fig siRNA_stochastic.png

Gillespie

function [ xx, XX, TT ] = SSA( x0, S, a, tt , param)
    %SSA Summary of this function goes here
    %   Detailed explanation goes here
    
    % initialise
    TT(1) = 0;
    XX(1,:) = x0;
    
    % step
    i = 1;
    while (TT(end)<tt(end));
        % increment step
        i = i + 1;
        
        %compute rates
        at = a(TT(i-1),XX(i-1,:),param);
        a0 = sum(at);
        
        for k = 1 : length(at)
            aj(k) = sum(at(1:k)/a0);
        end
        
        %sample time
        TT(i) = TT(i-1) + expinv(rand,1/a0);
        
        % select reaction that happens
        j = find(aj>rand,1,'first');
        
        % add reaction
        XX(i,:) = XX(i-1,:) + S(j,:);
    end

    xx = zeros(length(tt),length(x0));
    for j = 1:length(tt)
        xx(j,:) = XX(find(TT<=tt(j),1,'last'),:);
    end
    
end

Nuclease model script

% f = @(N,V,k) [p(3)* V  - p(4) * N , -p(1) * N * V  ];
g = @(p,y)    [p(3)* y(2)- p(4)*y(1); -p(1)*y(1)*y(2)];

%p= [  p1,  p2,  p3,  p4 ]; %insert the appropriate reaction rate constant
p = [   1, NaN,   1, 0.5 ];

[TOUT, YOUT] = ode45(@(t,y) g(p,y) ,[0,20],[0;1]);

plot(TOUT, YOUT(:,1), 'markersize', 15, 'linewidth', 5)
hold on; plot(TOUT, YOUT(:,2), 'r', 'markersize', 15, 'linewidth', 5); hold off

legend('Nuclease concentration','Vitality')
xlabel('time');
set(gca,'FontSize',24);
set(gcf,'position', [100 100 600 600]);

axis square
set(gcf,'Color','w')
export_fig nuc_pic.png

Team:TU-Munich/Modeling/Kill Switch

From 2013.igem.org

Kill Switch Modeling

Purpose

siRNA Model

Governing equations

Calculation of stable points and analysis

Result of our model

Interpretation

Stochastic Model

Nuclease Model

Governing equations

Calculation of stable points and analysis

Results of our model

Interpretation

Conclusions

MatLab Scripts

siRNA model script

Stochastic siRNA script

Gillespie

Nuclease model script

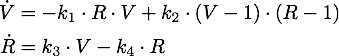
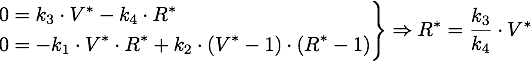
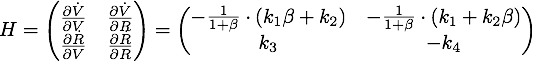
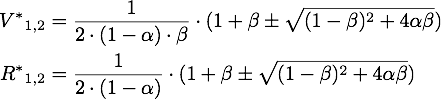
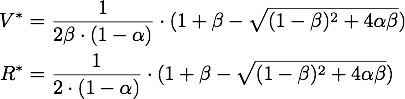
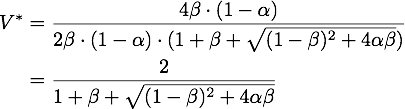
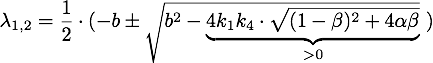
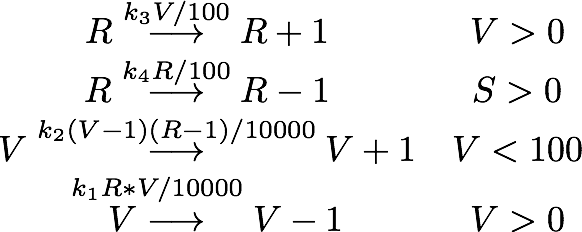
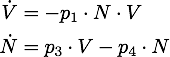
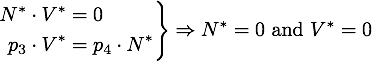
AutoAnnotator:

Follow us:

Address: