Team:Paris Bettencourt/Project/Sabotage/Model
From 2013.igem.org


Introduction
Synthetic biology relies on the addition of foreign genetic elements into organisms for their manipulation. This has the advantage to introduce orthogolous systems, avoiding many unwanted interactions with the organism's own processes citep{Guttinger2013}. However, every introduced system will consume cell's resources and compete for the molecular machinery responsible of replication (DNA level), transcription (RNA level), and translation (protein level). In case the device provides no direct benefit for the organism, the burden of the device will lead to a decrease in growth rate, and therefore a lower fitness citep{Shachrai2010}.
One way to avoid out-competition due to lower growth rate is by horizontal gene-transfer. Here we will study the behavior of a the phagemid/helpel system, which is a derived from from the non-lytic bacteriophage M13. This systems propagate through E. coli F+ populations via two vectors: a phagemid carrying the desired device, and a helper carrying the necessary machinery for production of the bacteriophage. Only when both vectors are present in a cell it will produce bacteriophage (see figure 1 below). Furthermore the system is designed such that the phagemid is produced in higher abundance than the helper.
We took the M13 infection model of cite{Wan2012} as a reference, and adapted to the phagemid/helper system. EXPLAIN SOMETHING ON RNA AND PROTEIN COSTS.
Notation: through this document we will use capital letter to denote cell populations, lower case to denote phagemid populations, and greek letters to denote functions and parameters.
Model
Cell populations can growth up to a maximum concentration that depends on the media, called carrying capacity (κc). Furthermore cells share the resources used for growth (S). Here following classic work in bacterial population dynamics we have chosen to represent bacterial growth as a logistic function (λ) together with an asymptotic dependency on the substrate concentration (β), commonly known as Monod's equation.
As we are interested in a chemostat-like system, all elements in the system will be subject to dilution due to eflow of media (with rate constant γ). Any other decay will be assumed to be negligible compared to eflow dilution. The addition of new media carrying substrate is coupled to the chemostat flow. The concentration of substrate added to the media is δ. To the right you can see the equations for n cell types (C)
Infection was assumed to follow mass action kinetics. This implies that the rate of infection is proportional to the phagemid (p) and a recipient cell (R). However, we need to account for the fact that M13 derived phagemid rely on the expression of the F-pili for infection, which is known to be less likely to be absent when resources are limited. For that, we have included the saturation function from Monod's equation into the infection rate. For simplification, we will assume that cells can get infected only by one phagemid. It is known that M13 infection inhibits the expresion of F-pili citep{Lin2011}.
M13 is a non-lytic phage, meaning that cells infected produce new phages without the need of lysing the cell. We will neglect any killing of cells due to infection. We will assume that cells have a delay in producing phages (F → F*) with constant rate τ. Then F* produce phages with constant maximal rate φ, which is modulated by the substrate concentration (β(S)). Finally, we know that phagemids are more likely to be produced that the helper. We called the ratio of production ψ.
Finally we have the following ODE describing the dynamics of our system.

The equations for M13 alone model are easy to infer by changing the number of infective elements and cells populations. More details please refer to the supplied Matlab scripts.

where θ is the concentration of substrate of half saturation, and κ is the carrying capacity.

where 1-α represents the relative reduction in maximal growth rate.

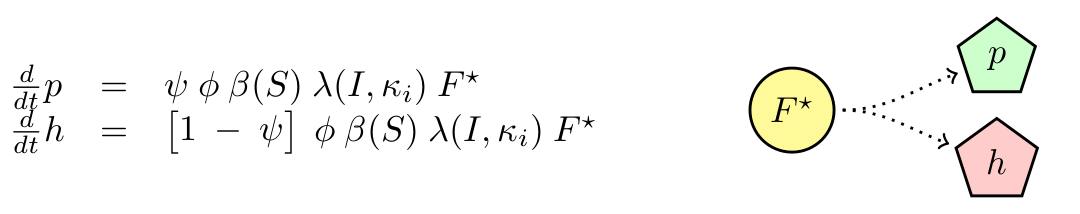

Figure 1:
| Variable | Description |
|---|---|
| R | Recipient (cells/ml) |
| P | Phagemid infected (cells/ml) |
| H | Helper infected (cells/ml) |
| F | Phagemid+helper infected inactive (cells/ml) |
| F* | Phagemid+helper infected active (cells/ml) |
| p | Phagemid (phages/ml) |
| h | Helper (phages/ml) |
| S | Substrate (a.u./ml) |
| Parameter | Units | Value | Source |
|---|---|---|---|
| μ | h-1 | 2.1 | cite{Wan2012} |
| αp | 0.99 | citep{Shachrai2010} | |
| αh | 0.6 | Assumed | |
| αf | 0.6 | cite{Wan2012} | |
| κc | cells ml-1 | 3e09 | cite{Wan2012} |
| θ | a.u. ml-1 | 1 | cite{Wan2012} |
| δ | a.u. ml-1 | ||
| ν | a.u. cells-1 | 3.5e-08 | cite{Wan2012} |
| κi | phages ml-1 | 2e11 | cite{Lin2011} |
| τ | h-1 | 2 | cite{Wan2012} |
| ι | ml phages-1 | 1e-08 | cite{Lin2011} |
| φ | phages cells-1 h-1 | 60 | cite{Lin2011} |
| ψ | 0.9 | Assumed | |
| γ | h-1 | Assumed |
Results
Introduction
Introduction
Introduction
Introduction
Introduction
Introduction
 "
"







 +33 1 44 41 25 22/25
+33 1 44 41 25 22/25


