Team:TU-Munich/Modeling/Filter

From 2013.igem.org

Revision as of 02:52, 29 October 2013 by ChristopherW (Talk | contribs)

(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)

Filter calculator

To simplify the testing of use cases and for the comfort of future users, we implemented a filter calculator. The filter calculator computes the number of remediation rafts needed to degrade a certain amount of pollutant in different environmental conditions. To do this we characterised the kinetics of the laccase at different pH values, temperatures and in different salt concentrations (see our kinetic fitting section for details). Alternatively you can enter the parameters of your own protein. For more information on how this is computed see the documentation below.

Figure 1: Work flow for the generation of transgenic moss.

Calculate number of remediation rafts

Select enzyme:

Select water way:

River flow rate [m³/s]:

Medium flow speed [m/s]:

Enter pH of water way:

Enter water temperature [°C]:

Enter salt concentration [M]:

Enter enzyme activity (k_cat/K_M) [M^-1s^-1]:

Enter enzyme half-life [h]:

Enter enzyme mass [Da]:

Subtrate concentration before filter [nM]:

Distance of downstream measurement after filter [km]:

Desired substrate concentration after filter in [nM]:

Filter model

Aim

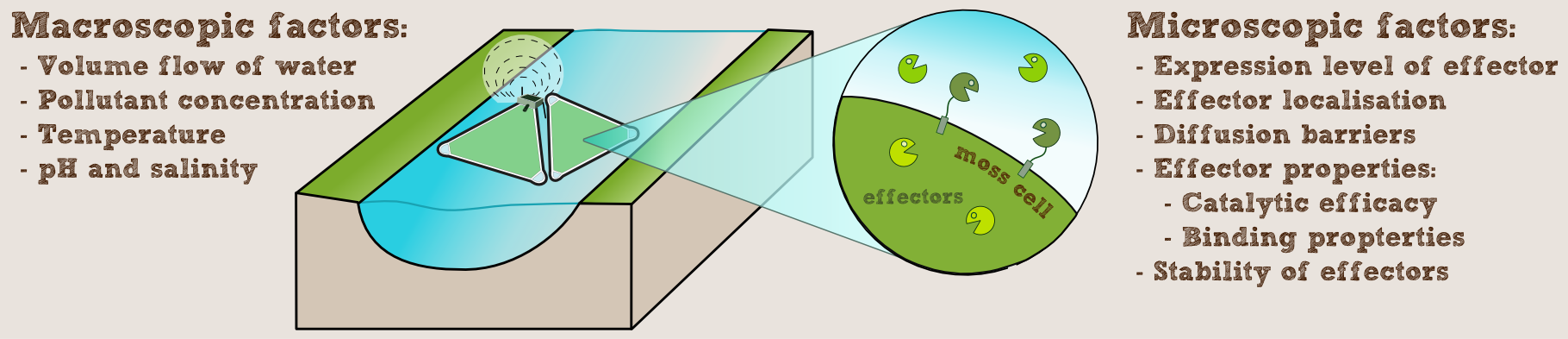
We wanted to know, how our PhyscoFilter could be used in practice and what kind of scale would be needed in a real-world implementation. So we looked at the some example water ways and waste water treatment plants, taking into account not only the local contamination, but also the characteristics of the water, such as pH, salt concentration and temperature, as well as flow speed and volume. To do this, we programmed an interactive calculator computing the required number of rafts for the given setup and provided example data for different use-cases with our laccase.

Model

To model this we assumed that the enzymes are secreted into the flowing water of the river or outflow of a waste water treatment plant. To determine the enzyme concentration we could achieve in this way, we questioned Prof. Reski and the experts of [http://www.greenovation.com Greenovation] (see our Expert council), a company using P. patens for the mass production of proteins for the pharmaceutical market. They told us, that in their experience fully grown moss produces 10-50 mg of protein per liter of liquid culture per day. For our computations we chose the conservative value of 25 mg per liter of culture per day.

Our remediation rafts (see our implementation page) have an area of slightly over 1 m², so taking into account the additional density due to the sedentary growth on the felt, we estimated this to roughly equal a liquid culture of 10 cm height, giving a culture volume of 100 liters per raft.

The price per raft is (also on our implementation page) about 50 $ including the setup. The optional Arduino controller providing live data on the current status of the filter, costs about 250 $, but you only need a single one for each filter location.

The enzymes produced in a day will be diluted in the amount of water flowing by in a day, so the initial enzyme concentration in the water is given by:

Now it must be taken into account, that the enzymes are inactivated over time, so given an inactivation rate λ or a half-life T_1/2, we have:

For the evolution of the substrate concentration we started with the well-known Michaelis-Menten formula and dropped the substrate concentration in the denominator, since the concentrations of the micro-pollutants found in the environment is always much smaller than the K_M values of the proteins, so we have the differential equation

.

Integration gives

By inverting this we get the formula below, showing how many rafts are necessary to reduce the substrate concentration by a specified amount

Since it is easier to work with the downstream distance along the river than with the time since the water passed the filter, we related the two according to .

pH and salt dependence

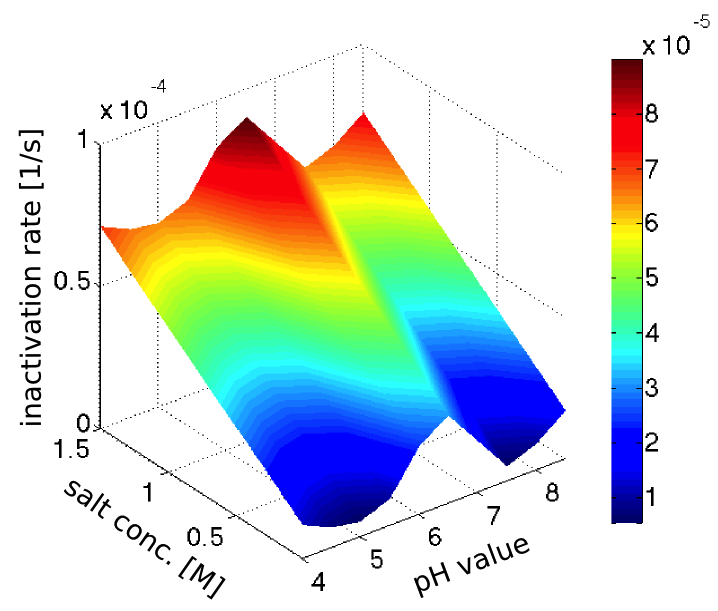
Figure 2: Laccase inactivation rate depending on pH and salt concentration

The inactivation rates of our enzyme in different pH-values and salt concentrations (see our enzyme kinetic fitting) were clearly not realistic, since the inactivation was too fast, and in strong disagreement with our assay of the laccase inactivation in river water. However the trends seemed sensible, so we decided to normalize the inactivation rates to fit with the half-life observed in the river water, which had pH 7.5 and a salt concentration of 0.28 mM (from this [http://www.isar-vils.de/downloads/Trinkasseranalyse%2017.06.2013.pdf water analysis]).

Assuming the inactivation rates to be additive, we obtained the plot in figure 2 showing the dependence of the inactivation rate on the pH-value and salt concentration.

River data values

As an example substrate to illustrate the calculator we chose the painkiller Diclofenac, which is widely used and very stable in the environment, hence reaching significant concentrations in the environment. It is tragically famous for being responsible for the near extinction of Indian vultures, in whose bodies high concentrations had accumulated after eating livestock excessively treated with Diclofenac. Diclofenac can be oxidised and hence inactivated by the laccase, so it is a great target for our PhyscoFilter.

The data on the Diclofenac pollution and the general characteristics of the rivers was obtained from: The Rhine in Germany: http://www.blac.de/servlet/is/2146/P-2c.pdf BLAC, 2003, http://undine.bafg.de/servlet/is/15706/ Monitory station Rhine, http://www.riwa-rijn.org/uploads/tx_deriwa/156_zoutrapport_08.pdf RIWA, 2008.

The Kaveri in India: http://link.springer.com/article/10.1007/s11356-013-1957-6 Shanmugam et al., 2013, http://www.hindawi.com/journals/chem/2008/234563/abs/ Begum and Harikrishnarai, 2008.

A large WWTP in Germany (Großlappen near Munich): http://www.blac.de/servlet/is/2146/P-2c.pdf BLAC, 2003, http://www.pts-umwelt-symposium.de/fileadmin/PTS/Umwelt Symposium/Dokumente/KW1_pdf.pdf Waste water treatment plant Großlappen report, http://www.isar-vils.de/downloads/Trinkasseranalyse 17.06.2013.pdf Report on drinking water in the area Isar-Vils.

Conclusion

As an example for a large waste water treatment plant in Germany the calculator tells us, that about 3000 remediation rafts are needed to reduce the Diclofenac (a painkiller, responsible for the near extinction of vultures in India) from the average value found there to levels below the suggested EU limit. This is quite a lot, but the area required would be less than half a football (i.e. soccer) pitch. For larger water ways, where the volume of the passing water dilutes the enzymes a lot, the calculator returns even higher numbers, which was to be expected. However, the activity of the laccase could be optimized and the literature values on the kinetics of the laccase from Bacillus pumilus vary widely both above and below our values. For example, http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3041658/ Thöny-Meyer et al., 2011 obtained a laccase activity for ABTS of 3.6 * 10⁶, so 20 times our estimate, which would greatly reduce the number of remediation rafts required. The model also illustrates very nicely the different dependencies, which play together in the complex degradation process combined with the enzyme inactivation. A good example the change in the required number of rafts, when the temperature is increased, indicating good applicability in warmer countries, such as India, but also potential problems in countries with high temperature amplitudes. All in all, the model shows, that this approach could work on water ways with higher concentrations and relatively low flow rates, but that some optimization is required to deal with large rivers, where the enzyme is extremely diluted.

Code:

The code for this calculator can be found here.

Diffusion model

Aim

With this model we wanted to get an idea of how the cell wall and the cell membrane would influence the diffusion of a pollutant. Additionally the aim was to investigate the effect of the enzyme localization on the filter efficiency.

Model

We simulated an idealized two-dimensional section of a cell with polluted water flowing past on the outside of the cell and pollutants diffusing inward through the cell wall and cell membrane. Then we added enzymes at the different locations our constructs support, namely in the cytoplasm, bound to the cell membrane or secreted into the intercellular space (assuming the protein is so large it does not pass through the cell wall).

Results

Figure 2 shows the animated evolution of the pollutant concentration in the absence of degrading enzymes and assuming the pollutant freely diffuses through the cell wall, while continuously pollutant is washed in from the left. As expected pollutant accumulates over time and will eventually reach the constant concentration of the in-flow.

Figure 3 and 4 show the simulation for cytoplasmic and intercellular enzyme localization respectively, again assuming free diffusion through the cell wall and keeping all other parameters (including the enzyme concentration) as before. The difference compared to Figure 2 is obvious and it is clearly visible (and intuitive), that the intercellular enzymes have a greater effect.

To show the further options of our program, the simulation of the effect of membrane bound enzymes with the cell wall impeding the diffusion of the pollutant is shown in Figure 5. However, since the enzymes are now spread out over a surface instead of a volume this is not properly comparable to the previous figures.

Figure 2: Simulation of pollutant concentration with freely diffusiable cell wall and no enzymes. Red indicates highest pollution, blue indicates no pollution.

Figure 3: Simulation of pollutant concentration with freely diffusiable cell wall and cytoplasmic enzymes (black circles). Red indicates highest pollution, blue indicates no pollution.

Figure 4: Simulation of pollutant concentration with freely diffusiable cell wall and intercellular enzymes (black circles). Red indicates highest pollution, blue indicates no pollution.

Figure 5: Simulation of pollutant concentration with permeable cell wall and membrane-bound enzymes (black circles). Red indicates highest pollution, blue indicates no pollution.

Conclusion

In general the model is not quantitative at the moment, because parameters like the diffusivity of the cell membrane etc. are very hard to determine. However, the simulations created give a good indication and a nice visualization of what is happening.

The Mathematics behind it

The evolution of the concentration of the pollutant is governed by the Advection-Diffusion-Equation describing the combination of advective, i.e. through movement of the medium, and diffusive transport of a substance in a medium such as water.

where D is the diffusion coefficient, v is the flow speed and R is the degradation rate of the enzymes, proportional to the concentration and the activity of the enzyme.

We approximated the right-hand side of this equation by breaking up the area into a finite grid and using finite differences (as shown [http://www.geometrictools.com/Documentation/FiniteDifferences.pdf here]). On the boundaries inside the cell we assumed that there is no concentration flow across, i.e. , where the vector n is normal to the boundary. To simulate the exchange across the membrane and where appropriate the cell wall, we used

where k is a constant proportional to the diffusivity of the membrane.

On the left boundary outside of the cell wall, the concentration was kept fixed simulating a constant inflow of pollutant. On the remaining boundaries the diffusive term across the boundary was dropped, since the advective flux is much greater than the diffusive one there.

The resulting differential equation in time was solved using a MatLab ODE solver.

Code

Main script: Diffusion model

filename = 'NoWallNoEnzyme.gif'; % where to save the output

xLength = 80; % must be an integer, but should be greater 20 for proper resolution, 
% but program takes approx. 1 minute at xlength=100 and time goes up rapidly

widthOfExtracellularSpace = 20; % must be an integer, same size constraints as above
widthOfIntercellularSpace = 10; % must be an integer
widthOfCytoplasmaticSpace = 20; % must be an integer

flowSpeed = 2; % speed with which fluid flows on outside of cell

diffusionWater = 0.005; % diffusion parameter in water

CellWallEffect = 0; % 0, if the cell wall does NOT impede diffusion at all
                    % 1, if the cell wall impedes diffusion
diffusionCellWall = 30; % diffusion parameter for the cell wall
% value NOT used, if CellWallEffect = 0, but needs some value for easier programming 

diffusionCellMembrane = 10; % diffusion parameter for the cell membrane

TimeHorizon =   5; % total time to be modeled
TimeSteps   = 0.2; % step size for the clip 
% (TimeHorizon/TimeSteps + 1 gives the total number of frames)

enzymeType = 0; %enzymeType takes the following values: 0 - for no enzymes
%                                                       1 - for cytoplasmic enzymes
%                                                       2 - for enzymes fixed to the membrane 
%                                                       3 - for enzymes in the intercellular space
enzymeRate = 100; % degradation rate of the enzymes, including concentration etc.


%=== CALCULATIONS FROM HERE ONWARDS, DO NOT CHANGE ANYTHING BELOW THIS LINE ===

totalWidth = widthOfExtracellularSpace + widthOfIntercellularSpace + widthOfCytoplasmaticSpace;

params = createParamVec(xLength,widthOfExtracellularSpace,widthOfIntercellularSpace,flowSpeed,diffusionWater,diffusionCellWall,diffusionCellMembrane,enzymeType,enzymeRate);

initialSetup = [[ones(widthOfExtracellularSpace,1);zeros(widthOfIntercellularSpace + widthOfCytoplasmaticSpace,1)],zeros(totalWidth,xLength-1)];

disp('Setup complete, beginning calculations. May take a few minutes')

if CellWallEffect == 1
    [TOut,YOut] = ode113(@(t,y) timeDeriv(y,params), 0:TimeSteps:TimeHorizon, reshape(initialSetup,totalWidth*xLength,1));
elseif CellWallEffect == 0
    [TOut,YOut] = ode113(@(t,y) timeDeriv_FreeWall(y,params), 0:TimeSteps:TimeHorizon, reshape(initialSetup,totalWidth*xLength,1)); 
else
    error('CellWallEffect must be either 0 (for perfect diffusion across wall) or 1 (for diffusion impeded by wall)')
end
    
disp('Calculations completed, generating output.')

input('Press Enter to produce the output! Do NOT click away till process is done')
for i = 1 : length(TOut)
    if (abs(min(YOut(i,:))) < 10^(-5)) % so there might be output in the negatives, but this is very small, so set it to 0 for the plot
        YOut(i,(YOut(i,:)<0)) = 0;
    end
    [~,h] = contourf(flipud(reshape(YOut(i,:),totalWidth,xLength)),0:0.01:1);
    
    set(h,'LineStyle','none'); % to make the output nicer
    
    rectangle('Position',[0,widthOfCytoplasmaticSpace-0.5,xLength,1],'FaceColor','k')
    rectangle('Position',[0,totalWidth-widthOfExtracellularSpace-0.5,xLength,1],'FaceColor','k')
    text(xLength/3,totalWidth - widthOfExtracellularSpace/2,'Extracellular Domain','FontSize',18);
    text(xLength/3,widthOfCytoplasmaticSpace + widthOfIntercellularSpace/2,'Intercellular Domain','FontSize',18);
    text(xLength/3,widthOfCytoplasmaticSpace/2,'Cytoplasmic Domain','FontSize',18);
    
    caxis([0 1]) % fix the colour scale
    
    if (enzymeType == 1) % cytoplasmatic degradation enzymes
        % draw enzymes in cyto
        rectangle('Position',[  xLength/4-2,  widthOfCytoplasmaticSpace/3-2,4,4],'Curvature',[1,1],'FaceColor','k');
        rectangle('Position',[2*xLength/4-2,2*widthOfCytoplasmaticSpace/3-2,4,4],'Curvature',[1,1],'FaceColor','k');
        rectangle('Position',[3*xLength/4-2,  widthOfCytoplasmaticSpace/3-2,4,4],'Curvature',[1,1],'FaceColor','k');
        rectangle('Position',[  xLength/4-2,2*widthOfCytoplasmaticSpace/3-2,4,4],'Curvature',[1,1],'FaceColor','k');
        rectangle('Position',[2*xLength/4-2,  widthOfCytoplasmaticSpace/3-2,4,4],'Curvature',[1,1],'FaceColor','k');
        rectangle('Position',[3*xLength/4-2,2*widthOfCytoplasmaticSpace/3-2,4,4],'Curvature',[1,1],'FaceColor','k');
    end
    
    if enzymeType == 2 % degradation enzymes localized on the cell mmbrane
        rectangle('Position',[  xLength/4-2,widthOfCytoplasmaticSpace-1,4,4],'Curvature',[1,1],'FaceColor','k');
        rectangle('Position',[2*xLength/4-2,widthOfCytoplasmaticSpace-1,4,4],'Curvature',[1,1],'FaceColor','k');
        rectangle('Position',[3*xLength/4-2,widthOfCytoplasmaticSpace-1,4,4],'Curvature',[1,1],'FaceColor','k');
    end
    
    if enzymeType == 3 % degradation enzymes transported into the intercellular space
        rectangle('Position',[  xLength/4-2,widthOfCytoplasmaticSpace +   widthOfIntercellularSpace/3-2,4,4],'Curvature',[1,1],'FaceColor','k');
        rectangle('Position',[2*xLength/4-2,widthOfCytoplasmaticSpace + 2*widthOfIntercellularSpace/3-2,4,4],'Curvature',[1,1],'FaceColor','k');
        rectangle('Position',[3*xLength/4-2,widthOfCytoplasmaticSpace +   widthOfIntercellularSpace/3-2,4,4],'Curvature',[1,1],'FaceColor','k');
        rectangle('Position',[  xLength/4-2,widthOfCytoplasmaticSpace + 2*widthOfIntercellularSpace/3-2,4,4],'Curvature',[1,1],'FaceColor','k');
        rectangle('Position',[2*xLength/4-2,widthOfCytoplasmaticSpace +   widthOfIntercellularSpace/3-2,4,4],'Curvature',[1,1],'FaceColor','k');
        rectangle('Position',[3*xLength/4-2,widthOfCytoplasmaticSpace + 2*widthOfIntercellularSpace/3-2,4,4],'Curvature',[1,1],'FaceColor','k');
    end
    set(gcf,'Color','w');
    
    drawnow
    frame = getframe(gcf);
    im = frame2im(frame);
    [imind,cm] = rgb2ind(im,256);
    if i == 1
        imwrite(imind,cm,filename,'gif', 'Loopcount',inf);
    else
        imwrite(imind,cm,filename,'gif','WriteMode','append');
    end
    
    
end

% movie2avi(F,filename,'fps',5);

Sub function: Time Derivative with no effect of cell wall on pollutant

function [ concChange ] = timeDeriv_FreeWall( concVector, parameterVector )
%timeDeriv_FreeWall - gives the time derivative of the concentration, when
%the wall does NOT impede diffusion

% parameterVector = [100,40,20,1,1,0.5,0.002];

%% Setup
length = parameterVector(1);
N = length; %grid size
totalWidth = size(concVector,1)/length;
outerWidth = parameterVector(2);
interWidth = parameterVector(3);
cytoWidth = totalWidth - outerWidth - interWidth;

u = parameterVector(4); %flow speed

D          = parameterVector(5); %diffusion parameter in water
k_wall     = parameterVector(6); %diffusion parameter through cell wall
k_membrane = parameterVector(7); %diffusion parameter through cell membrane
%the diffusion parameters across the wall & membrane are given by:
%   permeability*surfaceArea/((1m^3)*thickness of the membrane)
%NOTE: surfaceArea DEPENDS ON N, but depends on NORMALIZATION (i.e. length scale of x-axis) 
%the extent in the not shown z-direction is taken to be 1m (1 meter)
%then the formula used for the cross membrane/wall diffusion is:
%   dc_inside/dt = - dc_outside/dt = ( permeability*surfaceArea/((1m^3) * thickness) ) * (c_outside - c_inside) 
%                = k_membrane * (c_outside - c_inside)

enzymeType = parameterVector(8); %0 for none, 1 for cytoplasmic, 2 for localized, 3 for intercellular space
enzymeRate = parameterVector(9); %reaction rate for the enzymes (including concentration)

%transform to matrix for better handling
c = reshape(concVector, totalWidth , length); %c the matrix of concentrations
cOuter = c(                        1 : outerWidth              , :);
cInter = c(           outerWidth + 1 : outerWidth + interWidth , :);
cCyto  = c(totalWidth - cytoWidth +1 : totalWidth              , :);

% cNew = zeros(totalWidth, length); %the new matrix for storing the output


%% Cores of the domains (i.e. non-boundary terms)

%OUTER DOMAIN
newOuterCore = D*(N^2)*(...
    cOuter(3:end,2:end-1) + cOuter(1:end-2,2:end-1) + cOuter(2:end-1,3:end) + cOuter(2:end-1,1:end-2) ...
    -4 * cOuter(2:end-1,2:end-1)... %approximation of Laplacian(c)
    )...
    - (u*N/2)*(...
    cOuter(2:end-1, 3:end) - cOuter(2:end-1, 1:end-2)... %approximation of dc/dx
    );

%INTER DOMAIN
newInterCore = D*(N^2)*(...
    cInter(3:end,2:end-1) + cInter(1:end-2,2:end-1) + cInter(2:end-1,3:end) + cInter(2:end-1,1:end-2) ...
    -4 * cInter(2:end-1,2:end-1)... %approximation of Laplacian(c)
    );

%CYTO DOMAIN
newCytoCore = D*(N^2)*(...
    cCyto(3:end,2:end-1) + cCyto(1:end-2,2:end-1) + cCyto(2:end-1,3:end) + cCyto(2:end-1,1:end-2) ...
    -4 * cCyto(2:end-1,2:end-1)... %approximation of Laplacian(c)
    );


%% Boundary terms

%OUTER DOMAIN
newOuterLeft  = zeros(outerWidth,1); %since it is constant = 1
newOuterRightCore = D*(N^2)*(...
    -2*cOuter(2:end-1,end) + cOuter(1:end-2,end) + cOuter(3:end,end))...
    -(u*N/2)*(...
    3*cOuter(2:end-1,end) - 4*cOuter(2:end-1, end-1) + cOuter(2:end-1,end-2) ...
    );
newOuterTopRight = -(u*N/2)*(3*cOuter(1,end) - 4*cOuter(1,end-1) + cOuter(1,end-2)); 
newOuterTopCore = D*(N^2)*(...
    - 2*cOuter(1,2:end-1) + cOuter(1,1:end-2) + cOuter(1,3:end)...
    )... 
    - (u*N/2)*(...
    cOuter(1,3:end) - cOuter(1,1:end-2)...
    );
newOuterBottomRight = D*(N^2)* (...
    cOuter(end-1,end) -2*cOuter(end,end) + cInter(1,end)...
    )...
    -(u*N/2)*(3*cOuter(end,end) - 4*cOuter(end,end-1) + cOuter(end,end-2)) ...
    ;
newOuterBottomCore  = D*(N^2)*(...
    cOuter(end-1,2:end-1) - 4*cOuter(end,2:end-1) + cOuter(end,1:end-2) + cOuter(end,3:end) + cInter(1,2:end-1)...
    )...
    - (u*N/2) * ( cOuter(end,3:end) - cOuter(end,1:end-2) ) ...
    ;


%INTER DOMAIN
newInterLeftCore  = D*(N^2)*(...
    -4*cInter(2:end-1,1) + 2*cInter(2:end-1,2) + cInter(1:end-2,1) + cInter(3:end,1)  );
newInterRightCore = D*(N^2)*(...
    -4*cInter(2:end-1,end) + 2*cInter(2:end-1,end-1) + cInter(1:end-2,end) + cInter(3:end,end) );
newInterTopLeft  = D*(N^2)* (...
    -4*cInter(1,1) + 2*cInter(1,2) + cInter(2,1) + cOuter(end,1) ...
    );
newInterTopRight = D*(N^2)* (...
    -4*cInter(1,end) + 2*cInter(1,end-1) + cInter(2,end) + cOuter(end,end)...
    );
newInterTopCore = D*(N^2)*(...
    -4*cInter(1,2:end-1) + cInter(2,2:end-1) + cInter(1,1:end-2) + cInter(1,3:end) + cOuter(end,2:end-1)...
    );
newInterBottomRight= D*(N^2)* (...
    -4*cInter(end,end) + 2*cInter(end,end-1) + 2*cInter(end-1,end) ...
    ) + ( k_membrane * (cCyto(1,end) - cInter(end,end)) ) ... % diffusion across the membrane
    ;
newInterBottomCore = D*(N^2)*(...
    -4*cInter(end,2:end-1) + 2*cInter(end-1,2:end-1) + cInter(end,1:end-2) + cInter(end,3:end) ...
    ) + ( k_membrane * (cCyto(1,2:end-1) - cInter(end,2:end-1)) )... % diffusion across the membrane
    ; 
newInterBottomLeft = D*(N^2)* (...
    -4*cInter(end,1) + 2*cInter(end,2) + 2*cInter(end-1,1) ...
    ) + ( k_membrane * (cCyto(1,end) - cInter(end,end)) ) ... % diffusion across the membrane
    ; 



%CYTO DOMAIN
newCytoLeftCore  = D*(N^2)*(...
    -4*cCyto(2:end-1,1) + 2*cCyto(2:end-1,2) + cCyto(1:end-2,1) + cCyto(3:end,1) );
newCytoRightCore = D*(N^2)*(...
    -4*cCyto(2:end-1,end) + 2*cCyto(2:end-1,end-1) + cCyto(1:end-2,end) + cCyto(3:end,end) ...
    );
newCytoTopLeft  = D*(N^2)* (...
    -4*cCyto(1,1) + 2*cCyto(1,2) + 2*cCyto(2,1) ...
    ) + ( k_membrane * (cInter(end,1) - cCyto(1,1)) ) ... % diffusion across the membrane
    ;
newCytoTopRight = D*(N^2)* (...
    -4*cCyto(1,end) + 2*cCyto(1,end-1) + 2*cCyto(2,end)...
    ) + ( k_membrane * (cInter(end,end) - cCyto(1,end)) ) ... % diffusion across the membrane
    ;
newCytoTopCore = D*(N^2)*(...
    -4*cCyto(1,2:end-1) + 2*cCyto(2,2:end-1) + cCyto(1,1:end-2) + cCyto(1,3:end) ...
    ) + ( k_membrane * (cInter(end,2:end-1) - cCyto(1,2:end-1)) ) ... % diffusion across the membrane
    ;
newCytoBottomRight= D*(N^2)*(...
    -4*cCyto(end,end) + 2*cCyto(end-1,end) + 2*cCyto(end,end-1) ...
    );
newCytoBottomCore = D*(N^2)*(...
    -4*cCyto(end,2:end-1) + 2*cCyto(end-1,2:end-1) + cCyto(end,1:end-2) + cCyto(end,3:end) ...
    );
newCytoBottomLeft = D*(N^2)*(...
    -4*cCyto(end,1) + 2*cCyto(end-1,1) + 2*cCyto(end,2) ...
    );


%% Put together cNew

cNewOuter = [                 newOuterLeft                         , [newOuterTopCore;newOuterCore;newOuterBottomCore] , [newOuterTopRight;newOuterRightCore;newOuterBottomRight] ];
cNewInter = [[newInterTopLeft;newInterLeftCore;newInterBottomLeft] , [newInterTopCore;newInterCore;newInterBottomCore] , [newInterTopRight;newInterRightCore;newInterBottomRight] ];
cNewCyto  = [[ newCytoTopLeft; newCytoLeftCore; newCytoBottomLeft] , [ newCytoTopCore; newCytoCore; newCytoBottomCore] , [ newCytoTopRight; newCytoRightCore; newCytoBottomRight] ];


%% add enzymatic activity

if enzymeType == 0
    cNewFull = [cNewOuter ; cNewInter ; cNewCyto];
elseif enzymeType == 1 % cytoplasmatic degradation enzymes
    cNewFull = [cNewOuter ; cNewInter ; cNewCyto - enzymeRate*cCyto];
elseif enzymeType == 2 % degradation enzymes localized on the cell membrane
    cNewInter(end,:) = cNewInter(end,:) - enzymeRate*cInter(end,:);
    cNewFull = [cNewOuter ; cNewInter ; cNewCyto];
elseif enzymeType == 3 % degradation enzymes transported into the intercellular domain
    cNewFull = [cNewOuter ; cNewInter - enzymeRate*cInter ; cNewCyto];
else
    error('enzymeType must be one of: 0 - for no enzymes /n 1 - for cytoplasmic enzymes /n 2 - for enzymes fixed to the membrane /n 3 - for enzymes in the intercellular space')
end


%% transform back to vector for output

concChange = reshape(cNewFull, size(concVector,1),1);

end

Sub function: Time Derivative with the cell wall as diffusion barrier for the pollutant

function [ concChange ] = timeDeriv( concVector, parameterVector )
%timeDeriv computes the time derivative of the concentration, when the cell
%wall impedes diffusion
%   concVector must be a COLUMN vector

%% Setup
length = parameterVector(1);
N = length; %grid size
totalWidth = size(concVector,1)/length;
outerWidth = parameterVector(2);
interWidth = parameterVector(3);
cytoWidth = totalWidth - outerWidth - interWidth;

u = parameterVector(4); %flow speed

D          = parameterVector(5); %diffusion parameter in water
k_wall     = parameterVector(6); %diffusion parameter through cell wall
k_membrane = parameterVector(7); %diffusion parameter through cell membrane
%the diffusion parameters across the wall & membrane are given by:
%   permeability*surfaceArea/((1m^3)*thickness of the membrane)
%NOTE: surfaceArea DEPENDS ON N, but depends on NORMALIZATION (i.e. length scale of x-axis) 
%the extent in the not shown z-direction is taken to be 1m (1 meter)
%then the formula used for the cross membrane/wall diffusion is:
%   dc_inside/dt = - dc_outside/dt = ( permeability*surfaceArea/((1m^3) * thickness) ) * (c_outside - c_inside) 
%                = k_membrane * (c_outside - c_inside)

enzymeType = parameterVector(8); %0 for none, 1 for cytoplasmic, 2 for localized, 3 for intercellular space
enzymeRate = parameterVector(9); %reaction rate for the enzymes (including concentration)

%transform to matrix for better handling
c = reshape(concVector, totalWidth , length); %c the matrix of concentrations
cOuter = c(                        1 : outerWidth              , :);
cInter = c(           outerWidth + 1 : outerWidth + interWidth , :);
cCyto  = c(totalWidth - cytoWidth +1 : totalWidth              , :);

% cNew = zeros(totalWidth, length); %the new matrix for storing the output


%% Cores of the domains (i.e. non-boundary terms)

%OUTER DOMAIN
newOuterCore = D*(N^2)*(...
    cOuter(3:end,2:end-1) + cOuter(1:end-2,2:end-1) + cOuter(2:end-1,3:end) + cOuter(2:end-1,1:end-2) ...
    -4 * cOuter(2:end-1,2:end-1)... %approximation of Laplacian(c)
    )...
    - (u*N/2)*(...
    cOuter(2:end-1, 3:end) - cOuter(2:end-1, 1:end-2)... %approximation of dc/dx
    );

%INTER DOMAIN
newInterCore = D*(N^2)*(...
    cInter(3:end,2:end-1) + cInter(1:end-2,2:end-1) + cInter(2:end-1,3:end) + cInter(2:end-1,1:end-2) ...
    -4 * cInter(2:end-1,2:end-1)... %approximation of Laplacian(c)
    );

%CYTO DOMAIN
newCytoCore = D*(N^2)*(...
    cCyto(3:end,2:end-1) + cCyto(1:end-2,2:end-1) + cCyto(2:end-1,3:end) + cCyto(2:end-1,1:end-2) ...
    -4 * cCyto(2:end-1,2:end-1)... %approximation of Laplacian(c)
    );


%% Boundary terms

%OUTER DOMAIN
newOuterLeft  = zeros(outerWidth,1); %since it is constant = 1
newOuterRightCore = D*(N^2)*(...
    -2*cOuter(2:end-1,end) + cOuter(1:end-2,end) + cOuter(3:end,end))...
    -(u*N/2)*(...
    3*cOuter(2:end-1,end) - 4*cOuter(2:end-1, end-1) + cOuter(2:end-1,end-2) ...
    );
newOuterTopRight = -(u*N/2)*(3*cOuter(1,end) - 4*cOuter(1,end-1) + cOuter(1,end-2)); 
newOuterTopCore = D*(N^2)*(...
    - 2*cOuter(1,2:end-1) + cOuter(1,1:end-2) + cOuter(1,3:end)...
    )... 
    - (u*N/2)*(...
    cOuter(1,3:end) - cOuter(1,1:end-2)...
    );
newOuterBottomRight = D*(N^2)* (... %here use dc/dy = 0 across membrane, since diffusion across is covered below 
    -2*cOuter(end,end) + 2*cOuter(end-1,end)...
    )...
    -(u*N/2)*(3*cOuter(end,end) - 4*cOuter(end,end-1) + cOuter(end,end-2)) ...
    + ( k_wall * (cInter(1,end) - cOuter(end,end)) ) ... % diffusion across the wall
    ;
newOuterBottomCore  = D*(N^2)*(...
    2*cOuter(end-1,2:end-1) - 4*cOuter(end,2:end-1) + cOuter(end,1:end-2) + cOuter(end,3:end) ...
    ) - (u*N/2) * ( cOuter(end,3:end) - cOuter(end,1:end-2) ) ...
    + ( k_wall * (cInter(1,2:end-1) - cOuter(end,2:end-1)) ) ... % diffusion across the wall
    ;


%INTER DOMAIN
newInterLeftCore  = D*(N^2)*(...
    -4*cInter(2:end-1,1) + 2*cInter(2:end-1,2) + cInter(1:end-2,1) + cInter(3:end,1)  );
newInterRightCore = D*(N^2)*(...
    -4*cInter(2:end-1,end) + 2*cInter(2:end-1,end-1) + cInter(1:end-2,end) + cInter(3:end,end) );
newInterTopLeft  = D*(N^2)* (...
    -4*cInter(1,1) + 2*cInter(1,2) + 2*cInter(2,1) ...
    ) + (k_wall * (cOuter(end,1) - cInter(1,1)) ) ... % diffusion across the wall
    ;
newInterTopRight = D*(N^2)* (...
    -4*cInter(1,end) + 2*cInter(1,end-1) + 2*cInter(2,end) ...
    ) + ( k_wall * (cOuter(end,end) - cInter(1,end)) ) ... % diffusion across the wall
    ;
newInterTopCore = D*(N^2)*(...
    -4*cInter(1,2:end-1) + 2*cInter(2,2:end-1) + cInter(1,1:end-2) + cInter(1,3:end) ...
    ) + ( k_wall * (cOuter(end,2:end-1) - cInter(1,2:end-1)) ) ... % diffusion across the wall
    ;
newInterBottomRight= D*(N^2)* (...
    -4*cInter(end,end) + 2*cInter(end,end-1) + 2*cInter(end-1,end) ...
    ) + ( k_membrane * (cCyto(1,end) - cInter(end,end)) ) ... % diffusion across the membrane
    ;
newInterBottomCore = D*(N^2)*(...
    -4*cInter(end,2:end-1) + 2*cInter(end-1,2:end-1) + cInter(end,1:end-2) + cInter(end,3:end) ...
    ) + ( k_membrane * (cCyto(1,2:end-1) - cInter(end,2:end-1)) )... % diffusion across the membrane
    ; 
newInterBottomLeft = D*(N^2)* (...
    -4*cInter(end,1) + 2*cInter(end,2) + 2*cInter(end-1,1) ...
    ) + ( k_membrane * (cCyto(1,end) - cInter(end,end)) ) ... % diffusion across the membrane
    ; 



%CYTO DOMAIN
newCytoLeftCore  = D*(N^2)*(...
    -4*cCyto(2:end-1,1) + 2*cCyto(2:end-1,2) + cCyto(1:end-2,1) + cCyto(3:end,1) );
newCytoRightCore = D*(N^2)*(...
    -4*cCyto(2:end-1,end) + 2*cCyto(2:end-1,end-1) + cCyto(1:end-2,end) + cCyto(3:end,end) ...
    );
newCytoTopLeft  = D*(N^2)* (...
    -4*cCyto(1,1) + 2*cCyto(1,2) + 2*cCyto(2,1) ...
    ) + ( k_membrane * (cInter(end,1) - cCyto(1,1)) ) ... % diffusion across the membrane
    ;
newCytoTopRight = D*(N^2)* (...
    -4*cCyto(1,end) + 2*cCyto(1,end-1) + 2*cCyto(2,end)...
    ) + ( k_membrane * (cInter(end,end) - cCyto(1,end)) ) ... % diffusion across the membrane
    ;
newCytoTopCore = D*(N^2)*(...
    -4*cCyto(1,2:end-1) + 2*cCyto(2,2:end-1) + cCyto(1,1:end-2) + cCyto(1,3:end) ...
    ) + ( k_membrane * (cInter(end,2:end-1) - cCyto(1,2:end-1)) ) ... % diffusion across the membrane
    ;
newCytoBottomRight= D*(N^2)*(...
    -4*cCyto(end,end) + 2*cCyto(end-1,end) + 2*cCyto(end,end-1) ...
    );
newCytoBottomCore = D*(N^2)*(...
    -4*cCyto(end,2:end-1) + 2*cCyto(end-1,2:end-1) + cCyto(end,1:end-2) + cCyto(end,3:end) ...
    );
newCytoBottomLeft = D*(N^2)*(...
    -4*cCyto(end,1) + 2*cCyto(end-1,1) + 2*cCyto(end,2) ...
    );


%% Put together cNew

cNewOuter = [                 newOuterLeft                         , [newOuterTopCore;newOuterCore;newOuterBottomCore] , [newOuterTopRight;newOuterRightCore;newOuterBottomRight] ];
cNewInter = [[newInterTopLeft;newInterLeftCore;newInterBottomLeft] , [newInterTopCore;newInterCore;newInterBottomCore] , [newInterTopRight;newInterRightCore;newInterBottomRight] ];
cNewCyto  = [[ newCytoTopLeft; newCytoLeftCore; newCytoBottomLeft] , [ newCytoTopCore; newCytoCore; newCytoBottomCore] , [ newCytoTopRight; newCytoRightCore; newCytoBottomRight] ];


%% add enzymatic activity

if enzymeType == 0
    cNewFull = [cNewOuter ; cNewInter ; cNewCyto];
elseif enzymeType == 1 % cytoplasmatic degradation enzymes
    cNewFull = [cNewOuter ; cNewInter ; cNewCyto - enzymeRate*cCyto];
elseif enzymeType == 2 % degradation enzymes localized on the cell mmbrane
    cNewInter(end,:) = cNewInter(end,:) - enzymeRate*cInter(end,:);
    cNewFull = [cNewOuter ; cNewInter ; cNewCyto];
elseif enzymeType == 3 % degradation enzymes transported into the intercellular space
    cNewFull = [cNewOuter ; cNewInter - enzymeRate*cInter ; cNewCyto];
else
    error('enzymeType must be one of: 0 - for no enzymes /n 1 - for cytoplasmic enzymes /n 2 - for enzymes fixed to the membrane /n 3 - for enzymes in the intercellular space')
end


%% transform back to vector for output

concChange = reshape(cNewFull, size(concVector,1),1);

end

References:

http://www.blac.de/servlet/is/2146/P-2c.pdf BLAC, 2003 Report on pharmaceuticals in the environment

http://undine.bafg.de/servlet/is/15706/ Monitory station Rhine Monitory station Karlsruhe for the river Rhine

http://www.riwa-rijn.org/uploads/tx_deriwa/156_zoutrapport_08.pdf RIWA, 2008 Report on pollution in the Rhine basin by RIWA Netherlands

http://link.springer.com/article/10.1007/s11356-013-1957-6 Shanmugam et al., 2013 Non-steroidal anti-inflammatory drugs in Indian rivers. Environmental Science and Pollution Research, July 2013

http://www.hindawi.com/journals/chem/2008/234563/abs/ Abida Begum and Harikrishnarai, 2008 Begum, A. and Harikrishnarai (2008). Study on the Quality of Water in Some Streams of Cauvery River. E-Journal of Chemistry, 5 (2008), Issue 2: 377-384.

http://www.pts-umwelt-symposium.de/fileadmin/PTS/Umwelt Symposium/Dokumente/KW1_pdf.pdf Waste water treatment plant Großlappen report Report about the Waste water treatment plant Großlappen

http://www.isar-vils.de/downloads/Trinkasseranalyse 17.06.2013.pdf Report on drinking water in the area Isar-Vils

http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3041658/ Thöny-Meyer et al., 2011 Reiss, R., Ihssen, J. and Thöny-Meyer, L. (2011). Bacillus pumilus laccase: a heat stable enzyme with a wide substrate spectrum. BMC Biotechnol., 11:9.

Team:TU-Munich/Modeling/Filter

From 2013.igem.org

Filter calculator

Calculate number of remediation rafts

Filter model

Aim

Model

pH and salt dependence

River data values

Conclusion

Code:

Diffusion model

Aim

Model

Results

Conclusion

The Mathematics behind it

Code

Main script: Diffusion model

Sub function: Time Derivative with no effect of cell wall on pollutant

Sub function: Time Derivative with the cell wall as diffusion barrier for the pollutant

References:

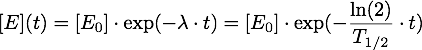
AutoAnnotator:

Follow us:

Address: