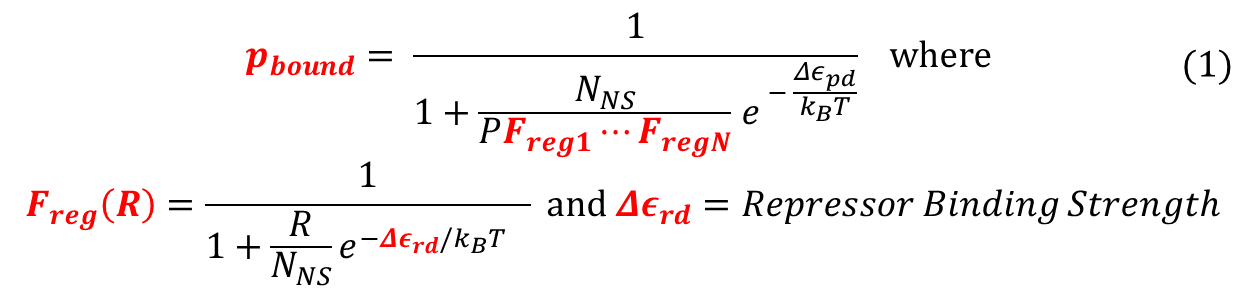Team:Duke/Modeling/Thermodynamic Model Application
From 2013.igem.org
Hyunsoo kim (Talk | contribs) (→Gene Expression Level vs. Number of Repressor Binding Sites) |
Cameronkim (Talk | contribs) (→Gene Expression Level vs. Binding Strength of Repressors) |
||
| (3 intermediate revisions not shown) | |||
| Line 50: | Line 50: | ||
[[File:Pbound_vs_kd.png|650px|center]] | [[File:Pbound_vs_kd.png|650px|center]] | ||
| - | <div align="center"> Figure 3. Relationship Between P<sub>bound</sub> vs. Kd </div> <br><br> | + | <div align="center"> Figure 3.3.3. Relationship Between P<sub>bound</sub> vs. Kd </div> <br><br> |
Similarly, the relationship between P<sub>bound</sub> and the dissociation constants of repressors was studied in this section. In addition to the variables and the values from previous section, a new set of variables were introduced to distinguish between weak and strong repressors. A value of 0.1nM was used for "Kd,strong" and this was the dissociation constant for strong repressors. Also, 10nM was used for "Kd,weak," which wass the dissociation constant for weak repressors. Because the strength of binding is represented as the "dissociation" constant, higher value translates to equilibrium shifting towards dissociated repressor ([DNA]+[Repressor]) instead of bound repressor ([DNA-Repressor]). | Similarly, the relationship between P<sub>bound</sub> and the dissociation constants of repressors was studied in this section. In addition to the variables and the values from previous section, a new set of variables were introduced to distinguish between weak and strong repressors. A value of 0.1nM was used for "Kd,strong" and this was the dissociation constant for strong repressors. Also, 10nM was used for "Kd,weak," which wass the dissociation constant for weak repressors. Because the strength of binding is represented as the "dissociation" constant, higher value translates to equilibrium shifting towards dissociated repressor ([DNA]+[Repressor]) instead of bound repressor ([DNA-Repressor]). | ||
| Line 57: | Line 57: | ||
[[File:Thermo_variables2_citation.png|650px|center]] | [[File:Thermo_variables2_citation.png|650px|center]] | ||
| - | <div align="center"> Figure 4. Variables for Strong and Weak Repressor Binding </div> | + | <div align="center"> Figure 3.3.4. Variables for Strong and Weak Repressor Binding </div> |
--> | --> | ||
<br> | <br> | ||
| Line 75: | Line 75: | ||
<br> | <br> | ||
[[File:Pbound_vs_kd_graph.png|750px|center]] | [[File:Pbound_vs_kd_graph.png|750px|center]] | ||
| - | <div align="center"> Figure 4. Graph of Fold Change in P<sub>bound</sub> vs. Combination of Weak (10nM) and Strong (0.1nM) Binding</div> <br><br> | + | <div align="center"> Figure 3.3.4. Graph of Fold Change in P<sub>bound</sub> vs. Combination of Weak (10nM) and Strong (0.1nM) Binding</div> <br><br> |
| - | Again, when a | + | Again, when a Hill function was fitted onto these data points using "cftool" command on MATLAB, the apparent Hill coefficient were determined and labeled next to each plot. As shown, the apparent Hill coefficient is lowest when the degree of unbalanced binding strengths is greatest, and is higher at both ends where the binding strengths at the five binding sites are equal. |
<br><br> | <br><br> | ||
| Line 113: | Line 113: | ||
#[https://2013.igem.org/Team:Duke/Modeling/Thermo_Derivation '''Derivation of the Thermodynamic Model'''] | #[https://2013.igem.org/Team:Duke/Modeling/Thermo_Derivation '''Derivation of the Thermodynamic Model'''] | ||
#[https://2013.igem.org/Team:Duke/Modeling/Codes '''MATLAB/Mathematica Codes Used'''] | #[https://2013.igem.org/Team:Duke/Modeling/Codes '''MATLAB/Mathematica Codes Used'''] | ||
| - | <br><br> | + | <br><br><br><br> |
</div> | </div> | ||
Latest revision as of 18:23, 27 September 2013
Contents |
Mathematical Modeling of Bistable Toggle Switch
Thermodynamic Model of Cooperative Repression
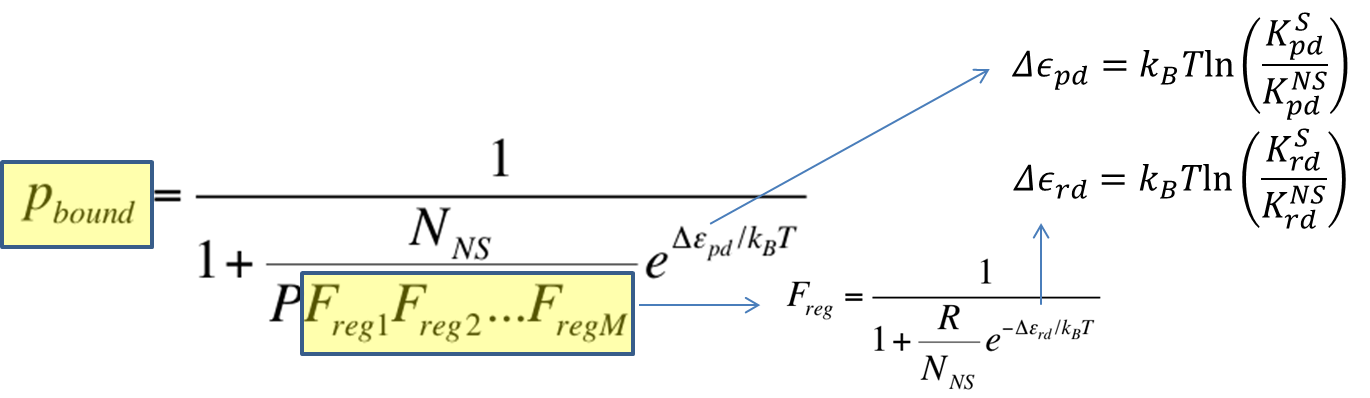
To recap the derivation from the previous section, the key equation for thermodynamic model of cooperative repression is:
In this section, the above model will be explored; specifically, the relationship between the red-colored terms will be studied. First, the relationship between Pbound and the number of Freg's will show the effect of changing number of binding sites on level of gene expression. Then, the relationship between Pbound and KSrd (Dissociation constant of repressor bound to DNA) will show the effect of changing binding strengths of repressors on level of gene expression.
Gene Expression Level vs. Number of Repressor Binding Sites
As highlighted in the equation shown above, the relationship between Pbound and the number of Freg's was studied. The variables and their values used are summarized below.
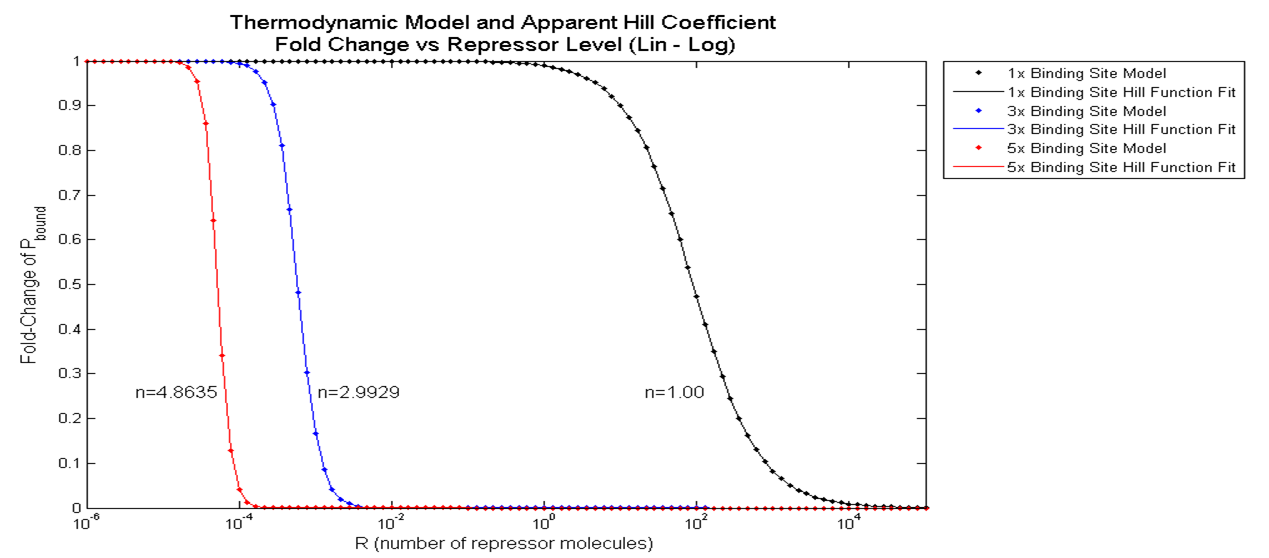
First, the basal level of Pbound was calculated using Freg = 1 (no Transcription Factors). Then, the Pbound values for the three cases--1 binding site, 3 binding sites, and 5 binding sites--were calculated for repressor level from 0.1 to 10,000 molecules/cell. Then finally, the Pbound values at these three cases were divided by the basal Pbound value to find the fold change in Pbound for the three cases. The results from these steps are graphed below.
The black, blue, and red data points indicate the fold change in Pbound when 1, 3 and 5 repressor binding sites are present. Qualitatively, it clearly looks like the slope of the hill function becomes steeper with additional binding sites. When a hill function was fitted onto these data points using "cftool" command on MATLAB, it was quantitatively shown that the apparent Hill coefficient increases from 1.00 to 2.99 then to 4.86 as the number of binding sites increased from 1 to 3, then to 5.
The significance of the result above is that a non-Hill equation that models the effect of multiple repressor sites on the probability of RNAP binding demonstrated increase in cooperativity with increasing number of binding sites.
Gene Expression Level vs. Binding Strength of Repressors
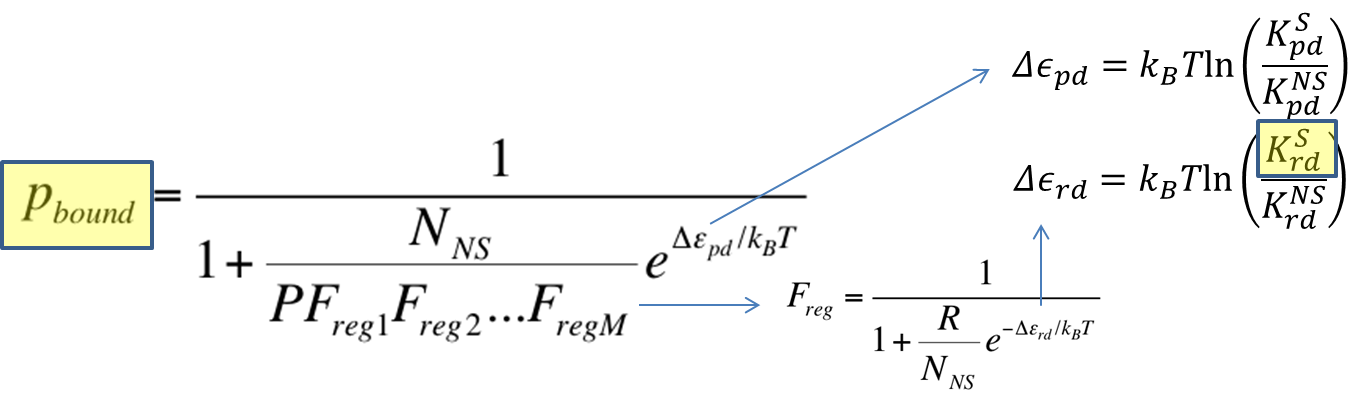
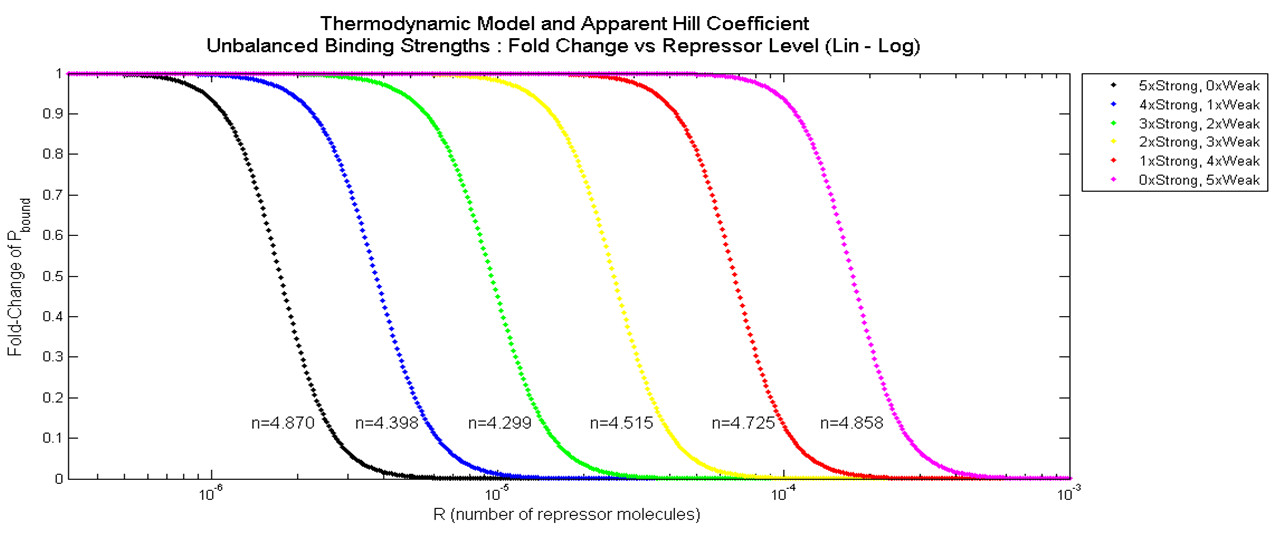
Similarly, the relationship between Pbound and the dissociation constants of repressors was studied in this section. In addition to the variables and the values from previous section, a new set of variables were introduced to distinguish between weak and strong repressors. A value of 0.1nM was used for "Kd,strong" and this was the dissociation constant for strong repressors. Also, 10nM was used for "Kd,weak," which wass the dissociation constant for weak repressors. Because the strength of binding is represented as the "dissociation" constant, higher value translates to equilibrium shifting towards dissociated repressor ([DNA]+[Repressor]) instead of bound repressor ([DNA-Repressor]).
Just like in the previous section, the basal level of Pbound was calculated using Freg = 1 (no Transcription Factors). The key difference was that there were two types of Fregs: one for strong binding and one for weak binding. The effect of different combinations of weak and strong binding was demonstrated by plotting the fold change in Pbound for 5 Binding sites for the following cases:
- 5 Strong Binding, 0 Weak Binding : Freg, total = (Freg, strong)5
- 4 Strong Binding, 1 Weak Binding : Freg, total = (Freg, strong)4 * (Freg, weak)
- 3 Strong Binding, 2 Weak Binding : Freg, total = (Freg, strong)3 * (Freg, weak)2
- 2 Strong Binding, 3 Weak Binding : Freg, total = (Freg, strong)2 * (Freg, weak)3
- 1 Strong Binding, 4 Weak Binding : Freg, total = (Freg, strong) * (Freg, weak)4
- 0 Strong Binding, 5 Weak Binding : Freg, total = (Freg, weak)5
The result of having different combinations of strong and weak binding for a promoter with 5 binding site is plotted below. Plots on the left have more strong binding sites (Black = 5 Strong, 0 Weak), and plots on the right have more weak binding sites (Pink = 0 Strong, 5 Weak).
Again, when a Hill function was fitted onto these data points using "cftool" command on MATLAB, the apparent Hill coefficient were determined and labeled next to each plot. As shown, the apparent Hill coefficient is lowest when the degree of unbalanced binding strengths is greatest, and is higher at both ends where the binding strengths at the five binding sites are equal.
An important conclusion that can be drawn from this result is that balanced repressor binding strengths among the battery of repressor binding sites is crucial for increasing cooperativity. Also, even though the dissociation constant of weak repressors was hundred times higher than that of strong repressors, the difference in apparent Hill coefficients was relatively small.
Now that we have demonstrated the effect of number of binding sites and binding strengths on cooperativity using a thermodynamic model, we now move on to characterizing the effect of several parameters on the stability of a system using a Kinetic Model.
MATLAB Code
The MATLAB codes used for the thermodynamic model can be found here.
References
- Goffeau A, Barrel B.G, Bussey H, et al.: Life with 6000 genes. Science 1996, 274(5287):546-567.
- Lee T.I, Young R.A: Transcription of eukaryotic protein-coding genes. Annu Rev Genet 2000, 34:77-137. p.109.
- Bintu L, Buchler NE, Garcia HG, Gerland U, Hwa T, Kondev J,Kuhlman T, Phillips R: Transcriptional regulation by the numbers: models. Curr Opin Genet Dev 2005, 15:125-135.
- Record MT, Reznikoff WS, Craig ML, McQuade KL, Schlax PJ: Escherichia coli RNA polymerase (s70) promoters and the kinetics of the steps of transcription initiation. In Escherichia coli and Salmonella Cellular and Molecular Biology. Edited by Neidhardt FC et al. ASM Press, Washington DC; 1996:792-821.
- Meckler J.F, Bhakta M.S, Kim M.S, Ovadia R, Habrian C.H, Zykovich A, et al.: Quantitative analysis of TALE-DNA interactions suggests polarity effects. Nucleic Acids Res 2013, 41:4118–4128.
Modeling Pages
- Cooperativity and Hill Equation
- Thermodynamic Model: Introduction
- Thermodynamic Model: Application (You are here)
- Kinetic Model
Supplementary Materials
 "
"