Team:Evry/Modelmeta1
From 2013.igem.org
| (5 intermediate revisions not shown) | |||
| Line 40: | Line 40: | ||
<ul> | <ul> | ||
<li>We can determine the iron-sensing delay of our bacteria</li> | <li>We can determine the iron-sensing delay of our bacteria</li> | ||
| - | <li>The model | + | <li>The model can be reused by other projects that include a FBS sensor</li> |
</ul> | </ul> | ||
</p> | </p> | ||
| Line 148: | Line 148: | ||
<th>Unit</th> | <th>Unit</th> | ||
<th>Description</th> | <th>Description</th> | ||
| - | |||
</tr> | </tr> | ||
| Line 156: | Line 155: | ||
<td>min^-1</td> | <td>min^-1</td> | ||
<td>Permeability of cell wall</td> | <td>Permeability of cell wall</td> | ||
| - | |||
</tr> | </tr> | ||
| Line 164: | Line 162: | ||
<td>M<sup>-1</sup>.s<sub>-1</sup></td> | <td>M<sup>-1</sup>.s<sub>-1</sup></td> | ||
<td>Formation constant of FeFur complex</td> | <td>Formation constant of FeFur complex</td> | ||
| - | |||
</tr> | </tr> | ||
| Line 172: | Line 169: | ||
<td>min<sup>-1</sup></td> | <td>min<sup>-1</sup></td> | ||
<td>FeFUR degradation rate</td> | <td>FeFUR degradation rate</td> | ||
| - | |||
</tr> | </tr> | ||
| Line 180: | Line 176: | ||
<td>min<sup>-1</sup></td> | <td>min<sup>-1</sup></td> | ||
<td>translation rate</td> | <td>translation rate</td> | ||
| - | |||
</tr> | </tr> | ||
| Line 188: | Line 183: | ||
<td>mol<sup>-1</sup></td> | <td>mol<sup>-1</sup></td> | ||
<td>Avogadro's constant</td> | <td>Avogadro's constant</td> | ||
| - | |||
</tr> | </tr> | ||
| Line 196: | Line 190: | ||
<td>m<sup>3</sup></td> | <td>m<sup>3</sup></td> | ||
<td>Volume of a bacterium</td> | <td>Volume of a bacterium</td> | ||
| - | |||
</tr> | </tr> | ||
| Line 204: | Line 197: | ||
<td>min<sup>-1</sup></td> | <td>min<sup>-1</sup></td> | ||
<td>mRNA degradation rate</td> | <td>mRNA degradation rate</td> | ||
| - | |||
</tr> | </tr> | ||
| Line 212: | Line 204: | ||
<td>min<sup>-1</sup></td> | <td>min<sup>-1</sup></td> | ||
<td>fixation rate of FeFUR</td> | <td>fixation rate of FeFUR</td> | ||
| - | |||
</tr> | </tr> | ||
| Line 220: | Line 211: | ||
<td>mM.min<sup>-1</sup></td> | <td>mM.min<sup>-1</sup></td> | ||
<td>Fur Production rate</td> | <td>Fur Production rate</td> | ||
| - | |||
</tr> | </tr> | ||
| Line 228: | Line 218: | ||
<td>-</td> | <td>-</td> | ||
<td>Sensor efficiency</td> | <td>Sensor efficiency</td> | ||
| - | |||
</table> | </table> | ||
</p> | </p> | ||
| Line 257: | Line 246: | ||
<h2>Models and scripts</h2> | <h2>Models and scripts</h2> | ||
<p> | <p> | ||
| - | This model was made using the Python language. You can <a href="https://static.igem.org/mediawiki/2013/ | + | This model was made using the Python language. You can <a href="https://static.igem.org/mediawiki/2013/1/1b/Sensormodel.zip"> download the python script here</a>. |
</p> | </p> | ||
| - | + | <!-- | |
<div id="citation_box"> | <div id="citation_box"> | ||
<p id="references"><b>References:</b></p> | <p id="references"><b>References:</b></p> | ||
| Line 267: | Line 256: | ||
</ol> | </ol> | ||
</div> | </div> | ||
| - | + | --> | |
Latest revision as of 03:34, 29 October 2013
Sensor Model
Introduction
In order to determine our Iron Coli's enterobactin production rate, we first have to know how much time our bacteria will take to sense the ambient iron. So, this first part of the Enterobactin production model focuses on the synthetic sensing system our team implemented in the bacteria.
Observations
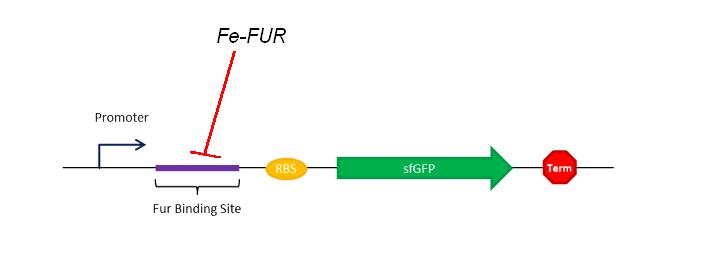
Naturally, when there is a large amount of iron in the environment, 2 iron ions complex with 2 FUR proteins and bind to the FUR Binding Site (FBS). This interaction regulate negativelly the genes downstream.
As shown on the Figure 1, our sensing system relies on a FBS. In order to easily model the sensing delay and analyse its results, the first construction is composed of a GFP placed right after the FBS.
Goals
Our goal in this part of the model is to create a generic FBS-related sensing model so that:
- We can determine the iron-sensing delay of our bacteria
- The model can be reused by other projects that include a FBS sensor
Materials and methods
From Iron to FBS:
The iron-FUR complex is simply formed that way:

We reduced this equation to:

Which is not annoying, since we just have to divide our [FeFur] by two to get the real complex concentration.
We can easily write down both the formation (v) and the dissociation (v') speeds:

We chose to model the iron input in the bacteria using a linear function of the external iron concentration Ferext, the factor p being the cell-wall permeability for iron.
The FUR on the other hand is produced by the bacteria. Its evolution can also be considered as linear, using a mean production rate of Fur0.


In this model, we only track the free Fe-FUR complex and not those attached to a FUR Binding Site. FBS is the number of inhibited Fur Binding Sites.

GFP expression:
To simulate the inhibition phenomenon, we chose to use our Logistic function under its differential form. Since it is the Fe-FUR that represses it, the LacI can be expressed as a logistic fuction of the Fe-FUR:

Ki1 is a non-dimensional parameter that repesents the inhibition power, and Kf is the fixation rate of the Fe-FUR on the FBS. Finally, Npla1 is the number of pasmids containing the GFP.
GFP Production:
The [mRNA] and [GFP] equations are alike. The prodction rates are Kr for the mRNA and Kp for the GFP. Since FBS represents the number of inhibited Fur Binding Sites, we have to substract it from Npla1.
Both variables also have a negative degadation term:

Tuning the model
The only parameter we couldn't find in the litterature is Ki1. Nevertheless, thanks to our construction and the experimental results we obtained with a plate reader, we can tune this parameter to obtain a realistic sensing model!
The Figure 2 is a set of experimental results showing the sensing efficiency for different iron concentrations. We can notice a substantial behaviour change between 10-4M and 10-5M of iron : the activity of our bacteria leaps at 10-5M.
Therefore, we ran simulations with different Ki1 values to try to determine the most fitting Ki1.
The Figure 3 shows that our model can lead to 3 different leaps, depending on the Ki1 value. The leap we are interested in is the 10-4M 10-5M leap.
We thus zoomed in, and performed the simulations with a more adapted range of Ki1.
The Figure 4 shows a more precise graph. It is with those simulation values that we calculated the most realistic Ki1, by maximizing the leap it creates. We also figured that the best fitting case requires the GFP reaching a plateau right after 10-5M of iron.
Finally, we set Ki1 at 6,3.10-5.
Results
The following results were computed using those parameters:
| Name | Value | Unit | Description |
|---|---|---|---|
| p | 0.1 | min^-1 | Permeability of cell wall |
| KFeFUR | 0.01 | M-1.s-1 | Formation constant of FeFur complex |
| Dff | 0.001 | min-1 | FeFUR degradation rate |
| Kp | 0.5 | min-1 | translation rate |
| NA | 6.02*1020 | mol-1 | Avogadro's constant |
| V | 6.5*10-16 | m3 | Volume of a bacterium |
| DmRNA | 0.001 | min-1 | mRNA degradation rate |
| Kf | 10-4 | min-1 | fixation rate of FeFUR |
| Fur0 | 0.01 | mM.min-1 | Fur Production rate |
| Ki1 | 6,3.10-5 | - | Sensor efficiency |
As shown in the Figure 5, there is a significant change in GFP production after 1000 seconds between the curve at 10-4M of iron and the one at 10-5M. The bacteria can thus sense low concentrations of iron.
Conclusion
The first construction of our team is fully modeled : we made a generic iron sensing model (with the FBS system).
Thanks to the experimental results we obtained with a plate reader, we were able to tune an unknown parameter to obtain a more realistic model.
This sensing model allowed us to continue the Enterobactin production model, the next step being the Inverter model.
Models and scripts
This model was made using the Python language. You can download the python script here.
 "
"