Logistic functions :

When we started to model biological behaviors, we realised very soon that we were going to need a function that simulates a non-exponential evolution, that would include a simple speed control and a maximum value. A smooth step function.

Such functions, named logistic functions were introduced around 1840 by M. Verhulst.

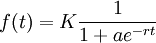
These functions looked perfect, but we needed more control : we needed to set a starting value and a precision.

Parameters:

• Q : Magnitude.
           The limit of g as x approaches infinity is Q.
• d : Threshold.
           The value of x from which we consider the start of the phenomenon.
• p : Precision.
           g(d)=Q*p Since the function never reaches 0 nor Q, we have to set an approximation for 0 or Q.
• k : Efficiency.
           This parameter influences the length of the phenomenon.

Differential form:

Let the following be a Cauchy problem:

The solution of this Cauchy problem is as below:
y(x) = K/(1+(K/p – 1)*e^-bx)

Here is our logistic function. Yet, differential equations are not always time-related. Let x be a temporal function, and y be a x-related logistic function. In order to integrate y into a temporal ODE, we need to write it differently:
dy/dx = by(x(t))(1 – y(x(t))/K) <=>( dy/dt)/(dx/dt) = by(x(t))(1 – y(x(t))/K)

And so:
dy/dt = dx/dt * by(x(t))(1 – y(x(t))/K) If t → x(t) is a continuous real function, then:
y(x(t)) = y(t) Finally,
dy/dt = dx/dt * by(1 – y/K)